La geometria de les còniques, sobretot amb la riquesa de possibilitats que ofereix Cabri, és tema d'un curs per si sola. Fins que no arribi, només veurem alguns fets bàsics sobre la determinació i la construcció d'aquestes corbes

Activitats

1. Qui passa per cinc punts?

Ja és prou conegut que dos punts determinen una recta i que tres punts determinen una circumferència. Deixem el cas de quatre per a més endavant i anem a veure que cinc punts determinen una cònica general

Ho veureu obrint la figura DETCON.FIG. Els punts A, B, C, D i E són aquells pels quals ha de passar la cònica i romanen fixos; el moviment del punt auxiliar W al voltant d'E farà que F descrigui la cònica. Aquesta s’obté, doncs, com a lloc geomètric de F quan W es mou.

Com s’ha fet aquesta construcció? És una conseqüència del teorema de Pascal aplicat a la cònica resultant i a l’hexàgon ADCBEF.

Els seus passos són:

- es tracen les rectes AD, CD i BE entre els punts donats
- les rectes AD i BE es tallen en el punt Y
- es traça la recta EW i es talla amb CD en el punt X
- es traça la recta XY i talla a BC en el punt Z
- es traça la recta AZ i talla a EW en F

Féu visible aquest lloc geomètric i observeu com es modifica al desplaçar els punts A, B, C, D i E.
 

2. Les còniques amb Cabri

El programa coneix la determinació de les còniques per cinc punts i la incorpora a l'eina Cònica del grup Corbes.

Proveu-la: planteu cinc punts al pla i, amb l'eina activada, cliqueu-los successivament. Si després els moveu, veureu com la cònica salta d'el·lipse a hipèrbola i a l'inrevès; la paràbola és un cas inestable i costa bastant de fer-la sortir sense premeditació.

Aquestes còniques estan una mica "orfes": no tenen focus, ni eixos, etc. No és pas qüestió de posar-los "a ull", però la geometria que requereix el seu traçat és bastant subtil.

L'element més simple que es pot obtenir d'una cònica és el seu centre. Obriu la figura CENTCON.FIG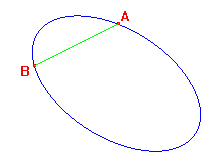

Veureu una el·lipse i una corda. Afegiu-hi dues cordes paral·leles a aquestes i traceu els punts mitjans de les cordes: veureu que estan alineats. Feu el mateix per a un conjunt de cordes paral·leles en una altra direcció. Les rectes dels punts mitjans es tallen en un punt, que és el centre de l'el·lipse.

Deformeu la figura a veure si el mètode serveix pr obtenir el centre d'una hipèrbola.

Hi ha macros preparades per a la resta d'elements. Les trobareu a la carpeta MACROS del material del curs, i són:

ASÍMPTOTES.MAC  fa les asímptotes d'una hipèrbola

EIXOS.MAC   fa els eixos d'una el·lipse o d'una hipèrbola

EIX_PARÀBOLA.MAC  fa l'eix d'una paràbola

FOCUS.MAC   fa els focus d'una el·lipse o d'una hipèrbola.
 
 

3. Qui passa per quatre punts?

Molta gent, però entre ella alguns objectes interessants:

(A) Una hipèrbola equilàtera

És a dir, una hipèrbola amb les asímptotes perpendiculars. La construcció és tan senzilla que queda a càrrec vostre: és suficient prendre com a cinc punts els quatre donats i l'ortocentre de qualsevol triangle que determinin.

Exercici 5
Exercici 6
 

(B) Dues paràboles

Aquesta construcció és complicada. La trobareu començada a la figura PARA4P.FIG. Per arribar-hi els passos han estat:

1) Es tallen les rectes AC i BD en el punt O
2) Es posa M en AC tal que OM és la mitjana geomètrica d'OA i OC.
3) Es posa N en BD tal que ON és la mitjana geomètrica d'OD i OB.
4) Es tracen els paral·lelograms OMEN i OMNE'.

Ara acabeu-la:

5) Obteniu la intersecció U de BC i AD i la intersecció V d'AB i CD.
6) La recta UV talla OE en K i OE' en K'.
7) Sigui I el punt mitjà entre O i K, i J el punt mitjà entre O i K'.
8) Els cinc punts A, B, C, D i I determinen una paràbola, i els cinc punts A, B, C, D, J determinen l'altra.

Si teniu paciència acabareu trobant la bonica figura

Resum

 

En aquesta pràctica heu d'aprendre: (A) La determinació de còniques per cinc punts i el seu motiu (B) Les corbes determinades per quatre punts (C) Les macroconstruccions auxiliars en l'estudi de les còniques.

 
__________________________________________________

Comentaris al marge

 
Si voleu construir una cònica d'un tipus determinat és millor que no ho feu com a lloc geomètric (mai queden ben acabades) ni fent-la passar per cinc punts. Serà millor que empreu aquestes quatre boniques macros:

EL:LIPSE_EIX_PUNT  fa una el·lipse a partir d'un segment i d'un punt sobre la mediatriu d'aquest

EL·LIPSE_EIX_FOCUS  fa una el·lipse a partir d'un segment i d'un punt sobre aquest com a focus

HIPÈRBOLA_EIX_FOCUS  fa una hipèrbola a partir d'un segment i d'un punt exterior a ell però sobre la mateixa recta com a focus

PARÀBOLA_FOCUS_DIRECTRIU fa una paràbola a partir del focus i de la directriu.