|
LLOCS I TRACES
Quan un punt genèric d’una construcció es desplaça, els altres punts derivats d’ell segueixen traces que són els seus llocs geomètrics. Moltes corbes usuals poden obtenir-se com a llocs geomètrics, i aquesta pràctica mostra les més senzilles.
|
|||
 |
Activitats
Un lloc geomètric és el conjunt de les posicions que pot adoptar un punt derivat de determinada construcció, quan es modifica un dels elements genèrics relatius d’aquesta. Cabri-Géomètre permet aproximar-se als llocs geomètrics per mitjà de traces. La traça d'un punt és el senyal que deixa en el seu moviment, necessàriament discontinu, i mancat de qualsevol qualitat geomètrica. Per veure un exemple obriu la figura LLOC1.FIG. A la figura hi ha una recta que pivota al voltant del punt X, un punt P i el seu simètric P' respecte la recta. Quin camí segueix P' si la recta gira al voltant de P? Preneu l'eina Traça activada / desactivada del grup Aspecte. Ara feu clic al punt P' i a continuació féu girar la recta. Us apareixerà la traça de P'.
Com veureu, té l'aspecte d'una circumferència. No podreu fer gran cosa amb la traça. Quan l'hagueu vist, esborreu-la
amb l'opció Regenerar dibuix del menú Edició.
2. Els llocs Però el programa també us deixa fer un traçat continu i més elegant del lloc geomètric d'un objecte que depèn del moviment d'un punt. El veureu a la figura LLOC2.FIG. Primer obriu-la i manipuleu-la una
mica per veure quins són els seus graus de llibertat. A continuació
preneu l'eina Lloc geomètric del grup Construccions
i feu clic en el segment i després en el punt X.
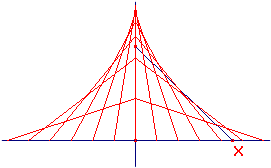 Aquest és el lloc geomètric d'un segment. El seu perfil és la meitat d'una corba bastant coneguda anomenada astroide. Per veure-la sencera, "destapeu" la part amagada amb Ocultar/Mostrar i veureu de seguida què us falta. El Cabri fa el lloc geomètric per juxtaposició de còpies de l'objecte. En principi en fa 50, però ho podeu canviar amb el menú Opcions, opció Preferències, pestanya Opcions per als llocs. Torneu a l'estat original de LLOC2.FIG i marqueu el punt mitjà del segment. Quin és el lloc geomètric d'aquest punt mitjà al moure X? Si esteu animats proveu amb aquests dos exemples més: (a) Preneu dos punts A i B en una circumferència. Preneu dos punts més X i Y de la circumferència de tal manera que XY sigui un diàmetre. Traceu els segments AX i BY, i feu la seva intersecció P. Quin és el lloc geomètric de P quan moveu el diàmetre XY? (b) Traceu una circumferència i en ella una corda AB que tingui la mateixa longitud que el radi. Preneu un punt C arbitrari sobre la circumferència i dibuixeu un punt D tal que ABCD sigui un paral·lelogram. Quin és el lloc geomètric de D quan C es mou sobre la circumferència? Quin és el lloc geomètric del centre del paral·lelogram? Ara podeu passar a l’Exercici 1 i a
l’Exercici 2
3. Les còniques Hi ha moltes corbes que poden ser definides com a llocs geomètrics. Les més populars són les còniques. Obriu la figura ELLIPSE.FIG. Traceu i mesureu FP i F’P. Mesureu el segment a i comproveu que en qualsevol posició és FP+F’P = a. Feu ara el lloc geomètric de P quan es desplaça X, i després feu el mateix amb P'. Obtindreu (aproximadament) l'el·lipse. Els punts F i F' són els seus focus i la longitud a és el seu eix major. Aquesta el·lipse no és cap meravella. A la pràctica 2 en veureu una molt millor. Modifiqueu el segment a i observeu "en viu" els canvis que experimenta l’el·lipse.
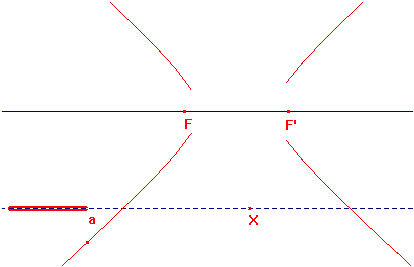
A continuació obriu la figura HIPERBOL.FIG. Traceu i mesureu FP i F’P. Mesureu el segment a i comproveu que en qualsevol posició és FP - F’P = a en valor absolut. Feu ara el lloc geomètric de P i de P' quan es desplaça X. Obtindreu (aproximadament) la hipèrbola. Els punts F i F’ són els seus focus i la longitud a és el seu eix real. Modifiqueu el segment a i observeu "en viu" els canvis que experimenta
la hipèrbola.
 En tercer lloc obriu la figura PARABOL. Traceu i mesureu els segments PX i PF, i dibuixeu el lloc geomètric de P quan X es mou. Obtindreu la paràbola. El punt F és el seu focus i la recta d és la seva directriu. 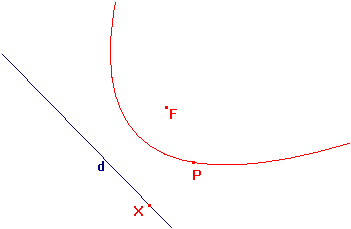
Resum
____________________________________________________________________
Aclariments i notes tècniques
A. Els llocs geomètrics al Cabri no són ben bé objectes
de ple dret. Es poden canviar de color i de gruix, es poden eliminar globalment,
i s'hi poden posar punts a sobre... en alguns casos; però no es
poden utilitzar, per exemple, per fer interseccions.
B. Hi ha llocs geomètrics de punts, segments i rectes,
com els que es veuran en aquest mòdul, però també
se'n poden fer de circumferències, semirectes, etc.
C. Quan un lloc geomètric resulta ser una circumferència,
no es disposa del seu centre directament. Cal construir-lo per mitjà
de dues mediatrius entre tres dels seus punts.
D. Per aplicar una transformació geomètrica del pla a
un lloc geomètric es pot emprar la següent astúcia:
es pren un "punt sobre objecte" P sobre el lloc geomètric, es transforma
P en P' i a continuació es fa el lloc geomètric de P' quan
P es desplaça.
E. A la pràctica 5 del mòdul 5 s'han invertit rectes i circumferències per mitjà de macroconstruccions. Per invertir qualsevol altre objecte respecte una circumferència es procedeix com en el cas anterior: es declara un punt sobre ell, s'inverteix i es fa el lloc geomètric del transformat. Les formes que s'obtenen són increïblement variades. Proveu-ho manipulant la figura INVTRI.FIG.
|