|
ACTIVITAT 4.8 |
|||
|
A l'activitat 2.10 hem vist que
vol dir expressar un vector En aquesta activitat estudiarem
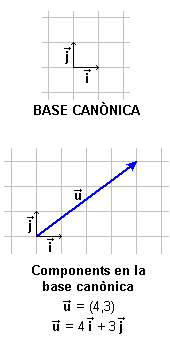
què passa si com a vectors Els vectors Segurament et preguntaràs com és que als components "habituals" d'un vector ara els diem components en la base canònica. Tingues paciència: la importància de tot el que hem explicat la veuràs en l'activitat següent, on veuràs que hi poden haver bases no canòniques i components d'un vector en una base no canònica. |
|
|
ACTIVITAT INTERACTIVA a) Dibuixa els següents vectors
donats com a combinació lineal dels vectors
b) Dibuixa els següents vectors
donats pels seus components en la base
SOLUCIÓ |
|
| PROPOSTA DE TREBALL |
| 1) Quins són els components
dels vectors 2) Com expressaries un vector donat en forma polar Ma com a combinació lineal dels vectors 3) Posa els vectors 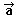 =530º, =530º, |
|
FI DE L'ACTIVITAT
4.8 |
|||