ACTIVITAT 4.10
BASES NO CANÒNIQUES I OBLIQÜES

Menú inicial
Activitat anterior

Menú de la unitat 4


A la figura de la dreta tens un exemple de base no canònica formada per dos vectors i que són unitaris, però no són perpendiculars; en aquest cas es pot dir que tenim una base obliqua.

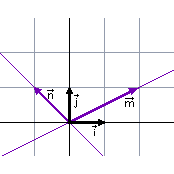
També en aquest cas, el vector es pot expressar de dues formes:
                                           = 1,3+ 2,9
                                           =  2 + 2
per tant, mentre que els components de en la base canònica , són
(1,3 , 2,9), els components deen la base no canònica , són (2,2).

La consideració d'aquestes bases obliqües sorprèn i sembla una cosa rebuscada en un món on s'imposa la rectangularitat (fulls de paper, quadres, portes, finestres, pantalles d'ordinador..., tot és rectangular). Observa que les bases obliqües apareixen senzillament quan substituïm rectangles per paral·lelograms.

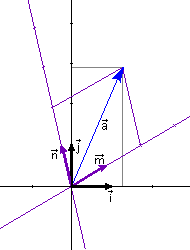
ACTIVITAT INTERACTIVA

A l'applet de la dreta tens dues bases dels vectors dels pla : la canònica i , i la i , de vectors unitaris, però no perpendiculars.

a) Dibuixa el vector=3+4 i observa els seus components en la base i .
b) Dibuixa el vector=-2+2 i observa els seus components en la base i .

Varia la base i (movent els punts P i Q) fins que l'angle xx' sigui de 15º, i l'angle x'y' de 120º . Aleshores:

c) Dibuixa el vector=4+3 i observa els seus components en la base i .
d) Dibuixa el vector=4- i observa els seus components en la base i .
                      SOLUCIÓ

PROPOSTA DE TREBALL
El cas més general d'una base no canònica es presenta quan està formada per dos vectors que no són ni unitaris ni perpendiculars (però recordeu que sí que han de ser no paral·lels i cap d'ells nul). Per exemple, els dos vectors i de la figura. Observa que = 2+ i = -+ , i aleshores es demana:
1) Si els components d'un vector en la base i són (3,-3), calcula els components de en la base i .
2) Si els components d'un vector en la base i són (-2,3), calcula els components de en la base i .
3) Representa les dues bases i els dos vectors i en un mateix gràfic.

FI DE L'ACTIVITAT 4.10
BASES NO CANÒNIQUES I OBLIQÜES

Menú inicial
Activitat anterior

Menú de la unitat 4