2. Seccionant la superfície cònica
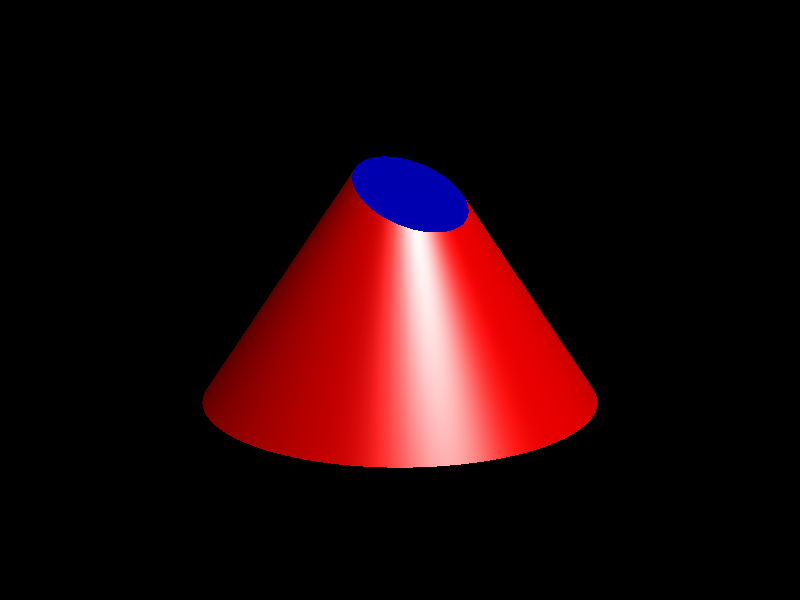
Ara presentarem les diferents formes o corbes que apareixen quan seccionem la superfície cònica amb un pla. Si el pla es perpendicular a l'eix, la secció és una circumferència. Hi ha un cas particular, que es dóna quan el pla passa pel vèrtex; en aquest cas, la secció es redueix a un punt, però aquesta possibilitat no té cap interès.
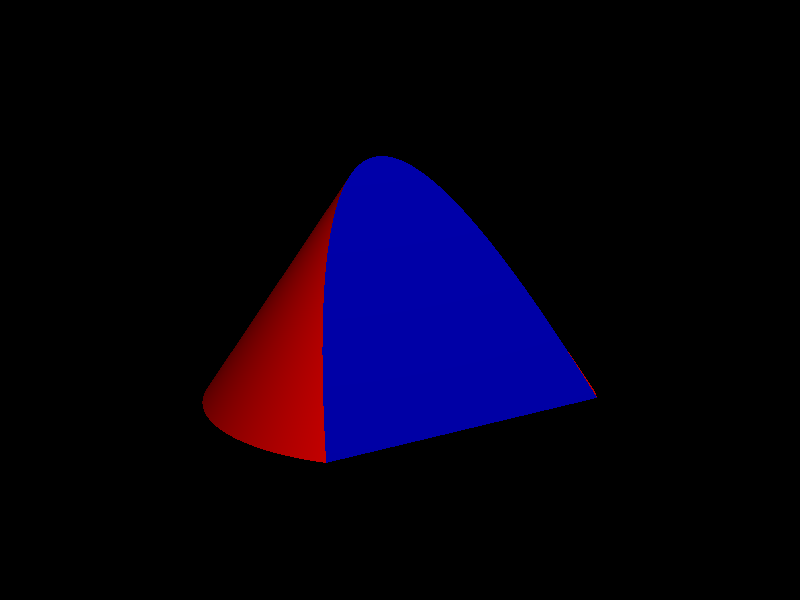
Si el pla no és perpendicular a l'eix i fa un angle amb l'eix superior al que fan eix i generatriu (que anomenarem obertura de la superfície cònica), obtenim una el·lipse. Aquí també hi ha un cas particular sense interès que es dóna (un altre cop) quan el pla passa pel vèrtex, i la secció que s'obté és simplement un punt.
Si el pla és paral·lel a la generatriu, és a dir, que l'angle entre el pla i l'eix coincideix amb l'obertura, obtenim una paràbola. Aquí també hi ha un cas particular sense interès que es dóna (un altre cop) quan el pla passa pel vèrtex, és a dir, quan el pla conté una de les posicions de la generatriu, i la secció que s'obté és simplement una recta: la generatriu.
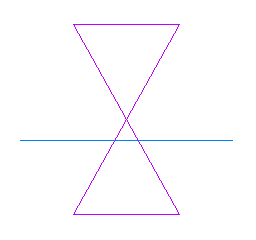
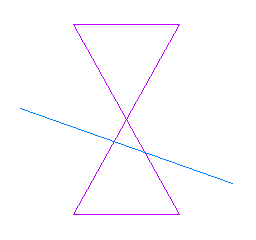
Si el pla no és perpendicular a l'eix i fa un angle amb l'eix inferior a l'obertura, obtenim una hipèrbola. Aquí també hi ha un cas particular sense interès que es dóna (un altre cop) quan el pla passa pel vèrtex, i la secció que s'obté són simplement dues rectes concurrents.
Les imatges de les seccions còniques s'han creat amb el programa POVRAY. Les altres s'han creat amb el programa gnuplot.
Copyright © Jaume Serra Nogués, 2006.
|