3. Les relacions mètriques de les seccions còniques
3.1 La circumferènciaConsiderem que A és el punt de tall entre l'eix i la generatriu, b és l'angle entre l'eix i la generatriu. Si el pla talla perpendicularment a l'eix, i ho fa pel punt C, per simetria, tots els punts P de la circumferència verifiquen que AC · tan b és constant, valor que es coneix com radi. Per això es pot definir una circumferència com el lloc geomètric dels punts que estan a una distància constant d'un punt fix.
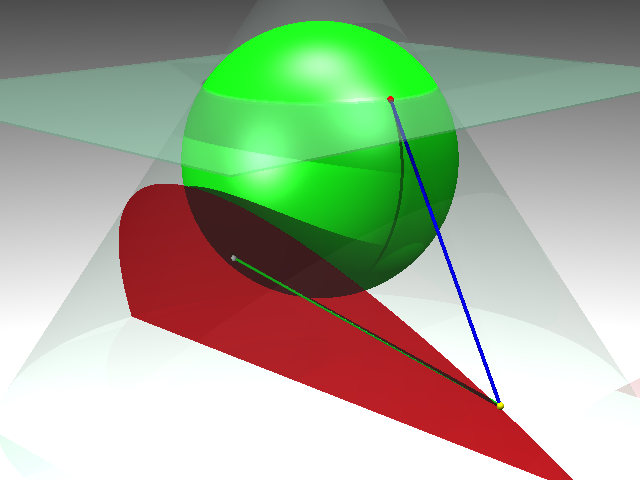
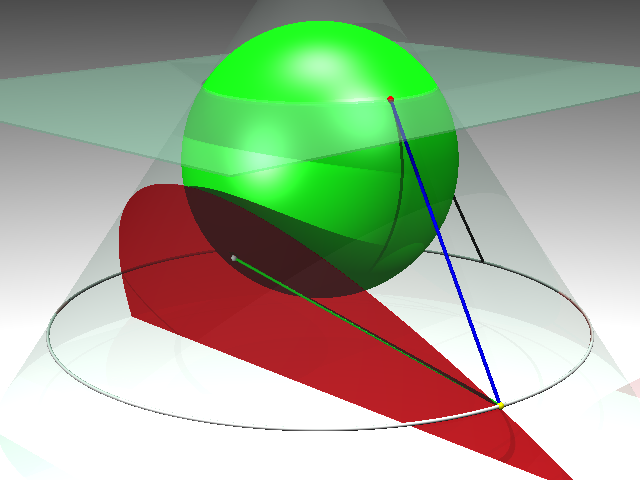
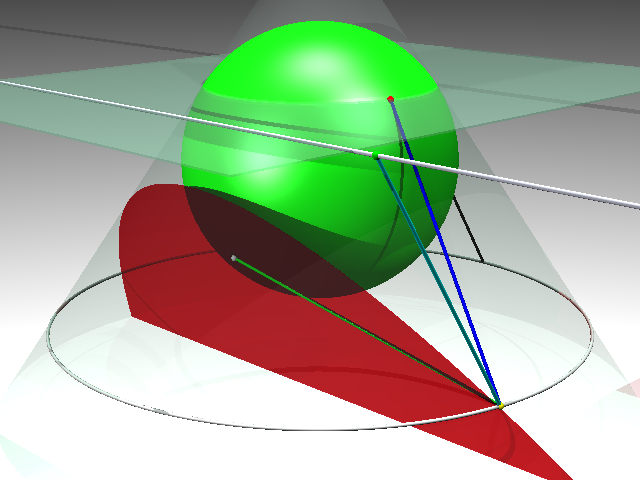
3.2 L'el·lipseSi el pla ja no és perpendicular a l'eix, i l'angle que fa amb l'eix és major que l'obertura de la cònica, generem una el·lipse. Considerem dues esferes tangents interiors a la superfície cònica. Els centres d'aquestes esferes estan sobre l'eix, per la qual cosa la tangència entre cada esfera i la superfície cònica és una circumferència perpendicular a l'eix.
Considerem també que les dues esferes són tangents al pla que talla la superfície cònica.
Sigui P un punt de l'el·lipse (marcat en groc). Anomenem A el punt de la circumferència de tangència entre la superfície cònica i l'esfera gran que està en la mateixa generatriu que P (marcat en blau fosc). Anomenem B el punt de la circumferència de tangència entre la superfície cònica i l'esfera petita que està en la mateixa generatriu que P (marcat en blau fosc). Anomenem F i F' els punts de tangència del pla amb les esferes (gran i petita, respectivament, i els marquem en blanc).
La distància PF (en color groc) és igual a PA (en color vermell), perquè PF i PA són segments tangents a una mateixa esfera que tenen un extrem comú. Pel mateix motiu, la distància PF' (color verd) és igual a PB (color blau).
Com que les circumferències de tangència són paral·leles, la distància AB és constant; per tant, PA + PB és constant; i per tant, PF + PF' és constant. Per això es pot definir una el·lipse com el lloc geomètric dels punts tals que la suma de les distàncies a dos punts fixos és constant.
3.3 La paràbolaQuan l'angle que fa el pla amb l'eix és major coincideix amb l'obertura de la cònica, generem una paràbola. Considerem una esfera tangent interior a la superfície cònica. El centre d'aquesta esfera està sobre l'eix, per la qual cosa la tangència entre l'esfera i la superfície cònica és una circumferència perpendicular a l'eix.
Considerem un pla tangent a aquesta esfera i paral·lel a una de les posicions de la generatriu.
Considerem un pla perpendicular a l'eix i que conté la circumferència de tangència entre la cònica i l'esfera. La intersecció dels dos plans és la recta d.
Sigui F (en color blanc) el punt de tangència entre l'esfera i el primer pla (el que genera la paràbola). Sigui P un punt de la paràbola (color groc). Sigui A el punt que està a la mateixa generatriu que P i que està també a la circumferència de tangència (color vermell). Aleshores, PF (color verd) coincideix amb PA (color blau) per tractar-se de dos segments tangents a la mateixa esfera.
Considerem la circumferència perpendicular a l'eix, que està sobre la superfície cònica i que passa per P (en color blanc). Considerem la posició de la generatriu que és paral·lela al pla que genera la paràbola. Sigui M el punt d'aquesta generatriu que està sobre aquesta circumferència. Sigui N el punt que està sobre aquesta generatriu que està sobre la circumferència de tangència. Aleshores PA coincideix amb MN (en negre, mig amagat per l'esfera).
Traslladem paral·lelament (conservant l'orientació) el segment MN sobre el pla que genera la paràbola, de manera que un dels extrems sigui P. L'altre extrem serà P' (en color verd), un punt que està sobre la recta d. Per construcció MN coincideix amb PP' (en blau).
Resumint, que PF coincideix amb PP', o, el que és el mateix, la distància entre P i F coincideix amb la distància entre P i d. Per això es pot definir una paràbola com el lloc geomètric dels punts tals que la distància a un punt fix (el focus) és igual a la distància a una recta fixa (la recta directriu).
3.4 La hipèrbolaQuan l'angle que fa el pla amb l'eix és menor que l'obertura de la cònica, generem una hipèrbola. Considerem dues esferes tangents a la superfície cònica, una a cada banda del origen. Aquestes esferes també són tangents al pla que genera la hipèrbola.
Sigui un punt P de la hipèrbola (en color groc). Sigui A el punt de la mateixa generatriu que passa per P i que és tangent a l'esfera superior (no visible en aquesta figura). Sigui B el punt de la mateixa generatriu que passa per P i que és tangent a l'esfera inferior (en blau).
Sigui F el punt de tangència entre l'esfera superior i el pla. Sigui F' el punt de tangència entre l'esfera inferior i el pla (dibuixats en blanc).
Alesores, PF (blau clar) coincideix amb PA (vermell) per ser segments tangents a una mateixa esfera; igual passa amb PB (vermell el segment PA i groc el segment AB) i PF' (blanc).
Sigui quina sigui la generatriu per on passa P, els corresponents punts A i B estan sempre sobre circumferències paral·leles, per la qual cosa AB (en groc) és constant. En resum, que la diferència entre PF i PF' sempre és AB. Per això es pot definir una hipèrbola com el lloc geomètric dels punts tals que la diferència de les distàncies a dos punts fixos (els focus) és constant.
Les imatges de les seccions còniques s'han creat amb el programa POVRAY. Les altres s'han creat amb el programa gnuplot.
Copyright © Jaume Serra Nogués, 2006.
|