5. Generant les còniques amb cordill

En aquest apartat mostrarem com podem generar les còniques amb ajut d'un cordill i d'alguns estris de dibuix. Al final, comentarem també algun procés per obtenir-les amb un progama de geometria dinàmica.

Les definicions mètriques de les còniques poden ser aprofitades per a crear-les amb ajut d'un cordill, alguns punts fixos, regle i escaire.

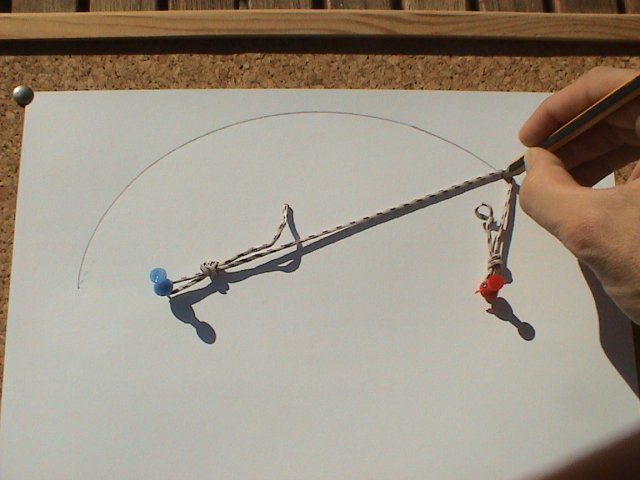
Per obtenir la circumferència necessitem un punt fix (el centre), i un cordill de la mida del radi. Lliguem un extrem del cordill al punt fix i l'altre extrem a l'estri que ens farà el traç.

Generant la circumferència.

Només cal moure el llapis mantenint tibant el cordill.

Generant la circumferència.

Per obtenir l'el·lipse, necessitem dos punts fixos (els focus), i un cordill de llargada superior a la separació dels dos focus. Lliguem cada extrem del cordill a un focus.

Generant l'el·lipse.

Posem el llapis en contacte amb el cordill de manera que quedi tibant, i només cal moure l'estri sense perdre la tibantor del cordill.

Generant l'el·lipse.

Per obtenir la paràbola necessitarem un cordill, un regle, un escaire i un punt fix. Un extrem del cordill anirà al punt fix i l'altre el subjectarem a l'escaire amb cinta adhesiva de manera que la llargada del cordill coincideixi amb la llargada de l'escaire.

Generant la paràbola.

Fem lliscar l'escaire sobre el regle (en aquest cas, el marc del suro) de manera que el llapis sembre estigui en contacte amb l'escaire i el fil alhora. Aquest muntatge assegura que la distància entre el punt de la paràbola (el llapis) i la recta directriu (el regle o el marc) coincideix amb la distància del punt al focus (on hem clavat la xinxeta).

Generant la paràbola.

Per generar la hipèrbola necessitem cordill, un regle i dos punts fixos. Un extrem del cordill el fixarem amb una xinxeta i l'altre el subjectarem al regle amb cinta adhesiva (podem deixar més o menys cordill, no hi ha una llargada fixa). L'altre punt fix el farem servir per subjectar el regle.

Generant la hipèrbola.

Anirem girant el regle i mantenint tibant el fil. El tras del llapis serà una hipèrbola. Anomenem A la xinxeta blava, B el lloc on hem subjectat el cordill al regle, P el lloc on està el llapis i C la xinxeta vermella. Aleshores, com que la llargada del cordill és sempre la mateixa (AP+BP=k₁) i la separació entre la xinxeta vermella i on subjectem el cordill al regle també (CP+BP=k₂), restant les dues condicions obtenim AP-CP=k₃.

Generant la hipèrbola.

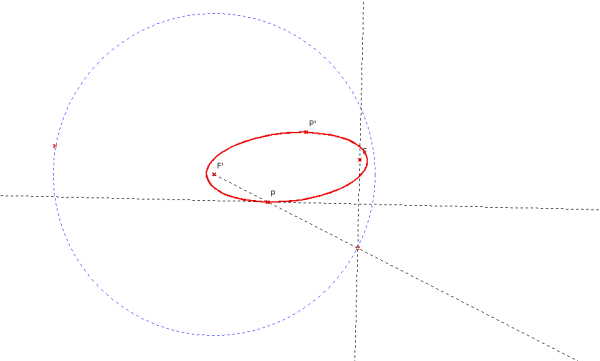
Amb un programa de geometria dinàmica

Per obtenir l'el·lipse, construim una circumferència amb centre O i que passi per C. Situem un punt A sobre la circumferència i un punt B interior a la circumferència.

Construim la recta OA i la mediatriu AB. Sigui P la intersecció d'aquestes dues rectes. Pel fet d'estar P sobre la mediatriu, d(P,B) = d(P,A). Per altra banda, d(O,A) és constant (és el radi), per tant d(O,P) + d(P,A) és constant. Substituint d(P,A) per d(P,B), obtenim que d(O,P) + d(P,B) és constant; és a dir O i B són els focus de l'el·lipse.

Generant l'el·lipse.

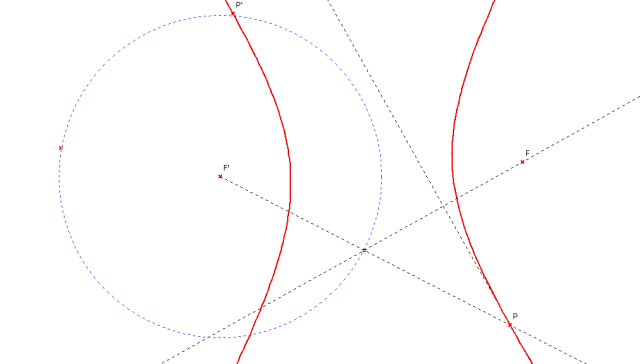
Per obtenir la hipèrbola, el procés és idèntic que amb l'el·lipse, amb l'única diferència que el punt B ha de ser exterior a la circumferència.

Construim la recta OA i la mediatriu AB. Sigui P la intersecció d'aquestes dues rectes. Pel fet d'estar P sobre la mediatriu, d(P,B) = d(P,A). Per altra banda, d(O,A) és constant (és el radi), per tant d(O,P) - d(P,A) és constant. Substituint d(P,A) per d(P,B), obtenim que d(O,P) - d(P,B) és constant; és a dir O i B són els focus de la hipèrbola.

Generant la hipèrbola.

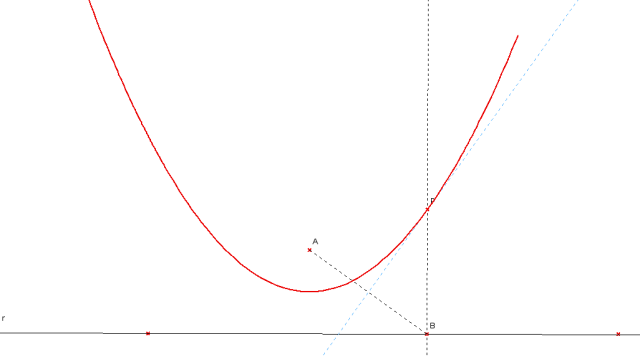
Per obtenir la paràbola construirem una recta r, un punt A exterior a la recta, i un punt B que es pugui moure sobre la recta.

Construirem una recta perpendicular a r que passi per B i la mediatriu entre A i B. La intersecció d'aquestes dues rectes serà el punt P. Pel fet d'estar P sobre la mediatriu, d(P,A) = d(P,B); com que P i B estan sobre la recta perpendicular, d(P,B) = d(P,r); per tant, P verifica que d(P,A) = d(P,r), és a dir A és el focus i r és la directriu.

Generant la paràbola.

Les imatges de les seccions còniques s'han creat amb el programa POVRAY. Les altres s'han creat amb el programa gnuplot.

Copyright © Jaume Serra Nogués, 2006.
Teniu permís per a copiar, distribuir i/o modificar aquest document en les condicions de la Llicència de Documentació Lliure del GNU, versió 1.1 o qualsevol versió posterior publicada per la Fundació per al Programari Lliure (Free Software Foundation), http://www.gnu.org/copyleft/fdl.html.