Exercicis
PAU-LOGSE: Camp gravitatori
|
| ENUNCIATS |
DADES |
RESULTATS |
1.
A quina distància de la Terra la gravetat es redueix
a una desena del seu valor a la superfície?
PAAU-LOGSE 98-99 |
RT=6400 km
|
13890
km
|
2.Si
el radi de la Terra quedés reduït a la meitat
però es mantingués la seva massa, quina seria
la intensitat del camp gravitatori sobre la nova superfície
terrestre? Es modificarien les òrbites dels satèl·lits
que giren al voltant de la Terra? Raoneu la resposta.
PAAU-LOGSE 97-98 |
No
|
4
go
No
|
3.
a) A
quina altura sobre la superfície de la Terra la gravetat
és la mateixa que sobre la superfície de la
Lluna;;
b) Quina
energia potencial gravitatòria respecte de la Terra
tindria una persona de 50 kg situada a aquesta altura?;
c) Amb
quina energia cinètica hauríem de llançar
un cos de 50 kg des de la superfície de la Terra perquè
arribés a aquesta altura amb velocitat nul·la?.
Suposeu negligible el fregament.;
PAAU-LOGSE 97-98 |
gLl=1,6m/s2;
RT=6400km;
MT =6,0.1024kg; G=6,67.10-11Nm2/kg2
|
a)
9,4.106m;
b)
-1,29.109J;
c)
1,87.109J
|
4.
Un astronauta dins d'un satèl·lit
en òrbita al voltant de la Terra a 250 km nota que
no pesa. ¿Això succeeix perquè és
negligible la gravetat a aquesta alçada o per un altra
raó?. Expliqueu-ho.
PAAU-LOGSE 96-97 |
No
|
No
|
5.
Un satèl·lit artificial
de massa 2000 kg està en òrbita circular al
voltant de la Terra a una altura de 3,6.106 m sobre
la superfície terrestre. Determineu:
a) La
relació entre la intensitat del camp gravitatori a
aquesta altura i el seu valor a la superfície terrestre.
b) Representeu
la força que actua sobre el satèl·lit
i calculeu-ne el mòdul. Sobre quin cos actuaria la
força de reacció corresponent? c) Quant valdrà
la velocitat del satèl·lit?
PAAU-LOGSE 97-98 |
RT=6400 km
MT =6.1024kg G=6,7.10-11Nm2/kg2
|
a)
g=0,41go
b)
8004 N, sobre la Terra
c)
6340 m/s
|
6.
Un satèl·lit artificial
de 100 kg de massa s'eleva fins a certa altura H de la superfície
terrestre. En aquesta posició s'encenen els coets propulsors,
que li comuniquen una velocitat de 7000 m/s, de forma que
el satèl·lit descriu òrbites circulars.
Calculeu:
a) L'altura
H de les òrbites del satèl·lit respecte
de la superfície de la Terra.
b) L'acceleració
del satèl·lit en la seva trajectòria
i el temps que tarda en fer 10 òrbites completes.
c) L'energia
mecànica del satèl·lit.
PAAU-LOGSE 97-98 |
RT=6400 km
MT =6.1024kg
G=6,7.10-11Nm2/kg2
|
a)
H=1,8.106m
b)
5,98 m/s2
20,4
h
c)
-2,45.109J
|
7.
Siguin dos satèl·lits
A i B de masses iguals m que es mouen en la mateixa òrbita
circular al voltant de la Terra, que té massa MT,
però en sentits de rotació oposats i, per tant,
en una trajectòria de xoc. El període de rotació
T, dels satèl·lits és de 24 h.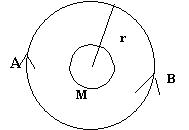 ; ;
a) Demostreu
que el radi de la trajectòria satisfà l'equació;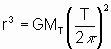 ; ;
b) Quines
són la velocitat i l'energia mecànica dels satèl·lits
abans del xoc?
c) Si
com a conseqüència del xoc, un satèl·lit
s'incrusta en l'altre, quina serà la velocitat del
cos de massa 2m després del xoc?
Quin
moviment seguirà després del xoc el cos de massa
2m que en resulta? Quant val la pèrdua d'energia mecànica?
PAAU-LOGSE 96-97 |
m=100kg
MT=5,98.1024kg
G=6,673.10-11Nm2/kg2
|
b)
3075 m/s; -4,7.108J
c)
el cos de massa 2m tindrà velocitat de 0 m/s;
i
caurà en mov. rectilini seguint el radi cap a la
superfície de la Terra, la pèrdua d'energia
mecànica és igual al treball de les forces
no conservatives
|
8.Un
satèl·lit de 2·103 kg de massa
gira al voltant de la Terra en una òrbita circular
de 2·104km de radi.
a) Sabent
que la gravetat a la superfície de la Terra val go=
9,8 m·s-2, quin serà el valor de
la gravetat en aquesta òrbita?
b) Quant
val la velocitat angular del satèl·lit?
c) Si
per alguna circumstància la velocitat del satèl·lit
es fes nul·la, aquest començaria a caure sobre
la Terra. Amb quina velocitat arribaria a la superfície
terrestre? Suposeu negligible l'efecte del fregament amb l'aire.
PAAU juny 00 |
RT =6370 km
|
a)
g/go = 0,99;
b)
2,23 10-4 rad/s
c)
9224 m/s
|
9.
Un satèl·lit artificial
de 2.000 kg de massa gira en òrbita circular al voltant
de la Terra a una altura h1=1300 km sobre la seva
superfície. A causa del petit fregament existent s’acosta
a la Terra lentament i després d’uns mesos, l’altura
sobre la superfície terrestre de la seva òrbita
circular s’ha reduït fins a h2=200 km. Es
demana:
a) La
relació g1/g2 entre els valors
del camp gravitatori terrestre en cadascuna de es dues òrbites
circulars.
b) La
relació v1/v2 entre les velocitats
del satèl·lit en cadascuna d’aquestes dues òrbites.
c) L’energia
potencial del satèl·lit en la segona òrbita.
PAAU setembre 00 |
RT = 6,4·106
m
MT = 6,0·1024kg
G=6,67·10-11Nm2 kg-2
|
a)
0,73
b)
0,93
c)
1,21.1011J
|