| Mòdul
6
|
Aplicacions
educatives de full de càlcul |
| Exercicis |
| Exercicis
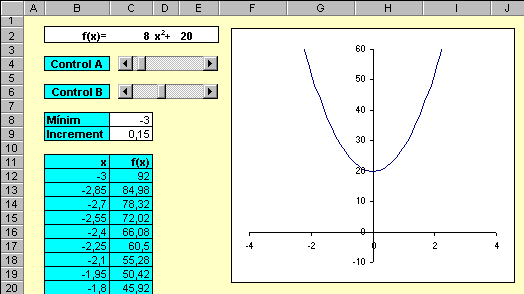
E61: Gràfica variable Us proposem que dissenyeu un full de càlcul que serveixi per representar gràfiques de funcions del tipus f(x) = Ax2 + B, amb la particularitat que els valors dels paràmetres A i B es puguin modificar amb dues barres de desplaçament com les utilitzades en la pràctica 1 d'aquest mateix mòdul. Una possible solució podria ser un full com el que reproduïm, en part, a continuació:
|
 |
|
|
Cal tenir en compte que la barra del control A ha d'estar connectada amb la cel·la C2, per fer variar el seu contingut. El mateix es pot dir sobre l'altra barra i la cel·la E2. En el rang B12:C52 es troben els valors de x i de f(x), a partir dels quals s'ha de fer la gràfica. Els valors de x (rang B12:C52) surten a partir del mínim de la cel·la C8 i de l'increment de la cel·la C9. Els valors d'aquestes dues cel·les no han de ser constants. Els valors de f(x) (rang C12:C52) surten d'aplicar la fórmula de la funció, que dependrà, naturalment, dels valors de les cel·les C2 i E2, el contingut de les quals, com hem dit abans, es modifica amb les barres de desplaçament. En definitiva, quan l'usuari faci servir les barres de desplaçament, podrà comprovar ràpidament l'efecte gràfic de la modificació dels valors dels paràmetres A i B. Cal tenir present que els valors d'aquests paràmetres no poden ser negatius perquè no s'admeten nombres negatius com a valors inicials o finals de les barres de desplaçament. Recordeu que, per tal que
tot funcioni bé, cal que l'opció Herramientas | Opciones
| Calcular | Automático estigui activada.
|
|
| E61bis (exercici
no obligatori)
Com a exercici voluntari us proposem ampliar l'anterior per tal que l'usuari pugui entrar els límits de variació de les barres de desplaçament per als paràmetres A i B i que puguin agafar valors negatius. El resultat podria ser semblant a:
Els límits de variació dels paràmetres A i B s'hauran d'entrar a les cel·les D4, E4, D7 i E7. En aquest cas, les barres de control ja no estan connectades amb les mateixes cel·les d'abans, sinó que es connecten a unes altres, els valors de les quals no són visibles. Els valors de les cel·les C2 i E2 són el resultat de fer una transformació dels valors mínim i màxim de les barres, segons els límits introduïts per l'usuari. E62: Finestres Ara us proposem que resoleu, fent servir les tècniques que heu practicat en la pràctica 3 d'aquest mateix mòdul, el problema següent: En una casa s'han d'instal·lar vidres en unes finestres de diferents formes i mides. L'empresa instal·ladora cobra el marc de cada finestra a 6,5 euros/metre, cada vidre a 10 euros/metre2 i per la feina d'instal·lació 20 euros.
|
|
| Un possible
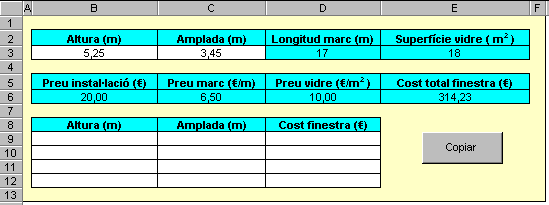
disseny del full de càlcul pot ser:
|
 |
|
El botó Copiar ha d'estar associat a una macro que vagi copiant les diferents solucions dels quatre apartats (trobades amb Solver) a les cel·les corresponents del rang B9:D12. E63: Filferro En aquest exercici us proposem que resoleu un problema de màxims i mínims, fent servir el Solver, així com heu fet en la pràctica 4 d'aquest mateix mòdul. Tenim un filferro de 300 metres de longitud per encerclar un terreny rectangular. Quines mides ha de tenir aquest terreny per tal que la seva àrea sigui el més gran possible? Un possible disseny del full de càlcul, sense haver trobat encara la solució, és:
En aquest cas, cal tenir present que per trobar la solució heu d'imposar la restricció que el perímetre (cel·la F3) sigui igual a la longitud del filferro. |
|
|
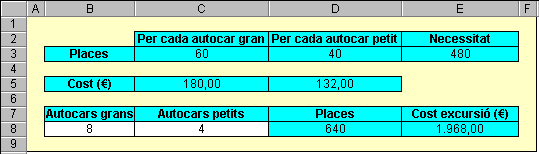
E64: Excursió En aquest exercici us proposem resoldre amb Solver un problema d'optimització similar al resolt en la pràctica 5 del mòdul actual. Volem organitzar una excursió per a 480 persones. Ens posem en contacte amb una empresa de transports que disposa de 6 autocars de 60 places i de 9 de 40 places. El lloguer d'un autocar gran costarà 180 euros i el d'un petit, 132 euros. Quants autocars de cada tipus hem de contractar per tal que l'excursió surti el més econòmica possible? Un possible disseny del full
de càlcul, abans de trobar la solució, és:
|
 |
|
Fixeu-vos que el valor de la cel·la E8 ha de ser mínim i que les cel·les que són variables són la B8 i la C8. No oblideu les restriccions degudes al nombre de places (és possible que algun autocar no vagi ple, però cap persona s'ha de quedar sense plaça), al nombre d'autocars disponibles (només podem disposar, com a màxim, de 6 autocars grans i 9 petits) i als caràcters positiu i enter del nombre d'autocars. |
|
|
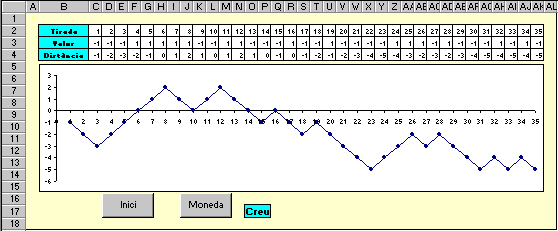
E65: Una passejada aleatòria (exercici no obligatori) Com a exercici voluntari us proposem, a continuació, que modifiqueu el full de càlcul que heu construït en la pràctica 7 d'aquest mòdul per tal que es pugui simular la passejada aleatòria que us expliquem tot seguit. Imagineu que una persona llança una moneda. Si surt cara fa una passa endavant i si surt creu fa una passa endarrere. Si repeteix els llançaments uns quants cops, s'anirà allunyant o apropant del punt de partida, segons els resultats del llançaments. Si simbolitzem amb nombres negatius la distància del punt de partida cap enrera i amb positius la corresponent distància cap endavant, podem fer un gràfic com el que surt a continuació en una possible solució de l'exercici:
|
 |
|
Si compareu aquesta figura amb la corresponent a la pràctica 7 d'aquest mòdul, us adonareu d'unes quantes diferències significatives:
La fórmula que ha d'estar en la cel·la C4 i que, amb el botó Moneda, s'ha d'anar copiant, pot ser =SI(C2=1;C3;B4+C3). Quan acabeu de fer servir el botó Moneda, és convenient que torneu a activar l'opció Herramientas | Opciones | Calcular | Automático per a futurs càlculs.
E66: Portada Com a últim exercici d'aquest mòdul, us proposem que dissenyeu una portada amb botons, similar a la treballada en la pràctica 7 d'aquest mòdul, de manera que permeti accedir a tots els altres exercicis. Cal que, en cada full de cada exercici hi hagi, també, un botó per tornar a la portada.
|