PRÀCTICA

 

LES RELACIONS D'INCIDÈNCIA


L’inventari de les relacions geomètriques s’inicia en aquesta pràctica amb les més senzilles: les relacions d’incidència.

 

Activitats

1. El teorema de Desargues

Les relacions entre objectes geomètrics poden ser relacions d’incidència o bé relacions mètriques. Les relacions d’incidència són l’objecte de la geometria projectiva.
 
 

 Un punt és incident amb una recta si el punt està en la recta, i una  recta és incident amb un punt si passa pel punt. Aquesta és una  relació primitiva de la geometria.

    Dues rectes són secants si hi ha un punt incident amb les dues, que és el seu punt d’intersecció. Si no és així les rectes són paral·leles.

    Tres punts són alineats si un és incident amb la recta que determinen els altres dos. Tres rectes són concurrents si el punt d’intersecció de dues és incident amb la tercera.

Tot i la seva simplicitat, les relacions d’incidència permeten formular alguns resultats importants.

Obriu la figura DESARG1.FIG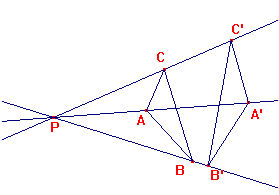

Els triangles ABC i A’B’C’ estan en perspectiva, i el punt P és el seu centre de perspectiva. 

La propietat més important dels triangles en perspectiva és el teorema de Desargues, que és l’objecte de l’ Exercici 5

El teorema de Desargues té un recíproc.
“Si els costats de dos triangles (o les seves prolongacions) es tallen en tres punts alineats, llavors els dos triangles estan en perspectiva”

La figura DESARG2 us mostra un exemple de dos triangles. Comproveu que verifiquen la hipòtesi d’aquest recíproc. Comproveu la tesi amb aquesta figura.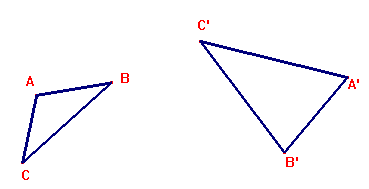

El teorema de Desargues és vàlid per al punt P “a l’infinit”
Exercici 6
 

2. El teorema de Pappus

Traceu dues rectes r i r’. Marqueu tres punts A, B i C a r, i tres punts A’, B’ i C’ a r’.
Traceu els segments AB’ i A’B, i el seu punt d’intersecció X. Traceu els segments AC’ i A’C, i el seu punt d’intersecció Y. Traceu els segments BC’ i B’C, i el seu punt d’intersecció Z.

Estudieu la relació entre X, Y i Z.. Formuleu i comproveu el resultat que observeu: és el Teorema de Pappus.

Si aquests dos teoremes us semblen interessants en trobareu més informació al llibre de B.I. Argunov i L.A. Skorniakov citat a la bibliografia
 
 
 

Resum

       
      En aquesta pràctica heu d'aprendre:

      (A) El llenguatge de les relacions d'incidència.

      (B) Els teoremes de Desargues i de Pappus.
_____________________________________________________________

Comentaris al marge

1. El paper dels teoremes de Desargues i de Pappus és crucial en l’algebraització de la geometria. A grans trets, el teorema de Desargues correspon a la propietat associativa i el teorema de Pappus a la propietat commutativa.

2. Aquests dos teoremes controlen el curiós tema de les construccions amb elements inaccessibles. Per exemple: com traçar la recta que passa per dos punts si en mig d'ells hi ha una zona que no es pot utilitzar per al dibuix?

3. Encara que sembli difícil de creure, dos triangles qualssevol poden moure’s fins que quedin en perspectiva. Això es pot comprovar amb Cabri-Géomètre, però donar un procediment de construcció no és elemental. Si algú ho vol provar...