| |
| |
 |
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
|
Ě Introducciˇ: |
|
| |
|
|
| |
S'entÚn per perspectiva c˛nica la
ciŔncia que el dibuixant fa servir per a representar la realitat dels
objectes tridimensionals que ens envolten en un pla de dues dimensions,
tal i com es veuen des d'un punt fix.
La perspectiva c˛nica es divideix en
Frontal i Obliqua.
Suposem que tots els objectes que es
representen en perspectiva poden ser encaixats en cubs o hexaedres,
aquests tenen les arestes de les seves cares formant angles de 90║,
degut a la seva forma els vŔrtex seran triedres trirectangles, Ús a dir
que tot hexaedre tindrÓ tres direccions en les seves lÝnies i aquestes
seran perpendiculars les unes a les altres.
Quan en la representaciˇ del cub,
dues d'aquestes rectes siguin paralĚleles al quadre, la tercera serÓ
perpendicular a aquest. Llavors es planteja una Perspectiva Frontal,
que Ús aquella en la que solament hi haurÓ un Punt de Fuga o conjunciˇ
de totes les lÝnies perpendiculars al quadre.
Quan nomÚs una d'aquestes rectes
Ús paralĚlela al quadre i les altres dues obliqŘes, o quan ho siguin les
tres, llavors es planteja una Perspectiva Obliqua.
|
|
| |

|
|
| |
|
|
|
Ě Perspectiva Frontal: |
|
| |
|
|
| |
Intervenen tres elements
fonamentals en el seu trašat: OBJECTE, QUADRE I SUBJECTE
L'objecte Ús el model que es
dibuixa, el quadre Ús la superfÝcie sobre la que es dibuixa i el
subjecte Ús el dibuixant.
|
|
| |
 |
|
| |
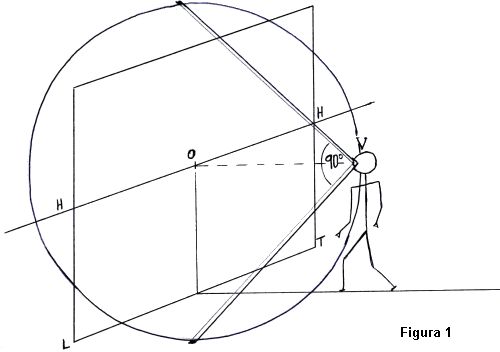
Imaginem-nos un home situat davant
d'un objecte que vol representar en un quadre, (figura 1). L'espai que
abasta la seva vista amb el cap imm˛bil representa en perspectiva un
angle de 90║ en forma c˛nica, el vŔrtex del qual Ús l'ull del pintor,
representat pel punt V, del qual surten una infinitat de raigs visuals;
un sol d'aquests raigs serÓ perpendicular al quadre. Aquest serÓ el raig
principal OV, que ens determinarÓ l'alšÓria de la lÝnia de l'horitzˇ
HH.
La part baixa del quadre que toca
a terra es diu LÝnia de Terra, Ús el segment LT.
|
|
| |
 |
|
| |
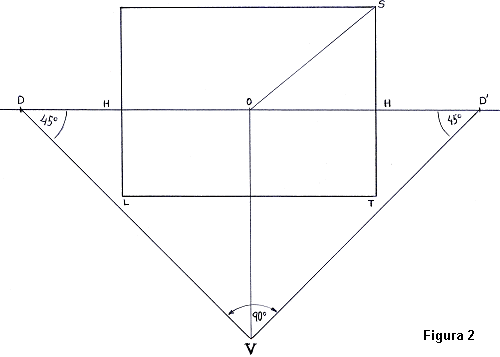
Com que l'angle visual Ús de 90║,
si l'observador o dibuixant vol abastar tot el quadre dins del seu camp
visual, s'haurÓ de situar a una distÓncia determinada del quadre.
DistÓncia que equivaldrÓ aproximadament entre una vegada i mitja i dues
vegades la longitud del segment OS, essent el punt O la
projecciˇ ortogonal de l'ull de l'observador i S el punt mÚs
allunyat del quadre (figura 2).
O sigui que entre1'5 vegades i 2
el segment OS en direcciˇ perpendicular al centre del quadre ens
donarÓ el punt de vista V. Per delimitar el camp visual trašarem
dos raigs visuals lÝmit que formin un angle de 45║ amb la perpendicular
OV, un per cada banda, fins a interceptar la lÝnia de l'horitzˇ
HH. AixÝ obtindrem els punts D i D' o de distÓncia,
els quals ens permetran representar mides exactes en el dibuix en
perspectiva.
Normalment els punts de distÓncia
quedaran fora del quadre, paper o lÓmina i caldrÓ utilitzar unes
extensions per situar els punts D i D' de manera que es puguin
trašar les lÝnies de distÓncia que ens daran les mesures en perspectiva
de les lÝnies perpendiculars al quadre (que es dirigeixen a V).
|
|
| |
|
|
| |
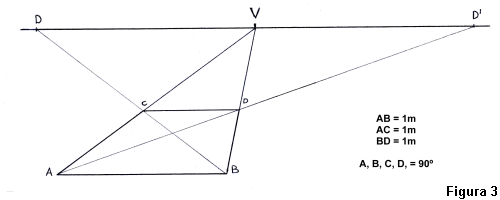
Les lÝnies paralĚleles al quadre
no pateixen cap deformaciˇ i mantenen la seva mida real, per˛ quan la
lÝnia Ús perpendicular al quadre pateix una deformaciˇ ˛ptica que podem
representar de manera mesurada a partir de la lÝnia paralĚlela al quadre
i a travÚs dels punts D i D' de distÓncia. (figura 3).
|
|
| |
Exercici d'exemple:
Traslladem segments mesurats des de la posiciˇ paralĚlela al quadre a la
posiciˇ perpendicular.
|
|
| |
|
|
| |
|
|
| |
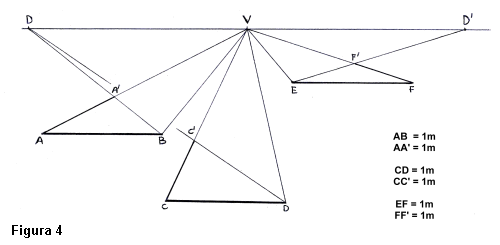
Si el segment perpendicular al
quadre Ús major o menor que el paralĚlel, partirem igualment d'ell per˛
li afegirem o li traurem el necessari per a poder traslladar la mida que
ens convingui, nomÚs amb la finalitat de trobar la distÓncia en
perspectiva. (lÝnies auxiliars) (fig .4)
|
|
| |
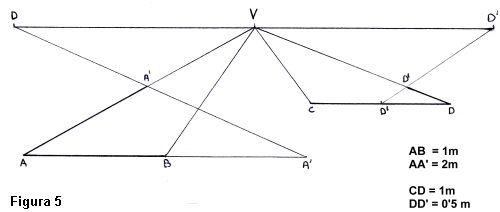
Exercici d'exemple:
Traslladem segments de diferent mida que els paralĚlels al quadre. (fig.
5) |
|
| |
|
|
| |

|
|
| |
|
|
|
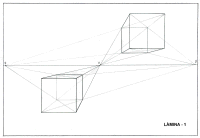
Ě LÓmines amb objectes
ortogonals: |
|
| |
|
|
| |
|
L└MINA 1 |
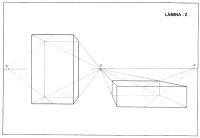
L└MINA 2 |
 |
 |
|
Construcciˇ d'un hexaedre regular
de 7 x 7 x 7 cm. en dues vistes, una per sota de l'horitzˇ i l'altra
per sobre. |
Construcciˇ
d'un prisma de base rectangular de 10 cm. d'alšÓria per 6 cm.
d'amplÓria i per 3 cm. de fons o gruix, en dues posicions, una
vertical i l'altre horitzontal. |
|
L└MINA 3 |
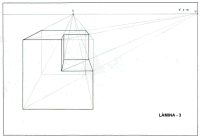
L└MINA 4 |
 |
 |
|
Representaciˇ d'un cub, oscat regularment en forma de cub pel seu
vŔrtex superior dret i fins a la meitat del seu costat, amb vista
lleugerament decantada cap a l'esquerra. |
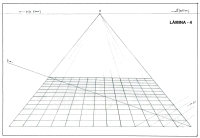
Representaciˇ d'un s˛l enrajolat
d'una cambra de proporcions quadrades. |
|
L└MINA 5 |
L└MINA 6 |
 |
 |
|
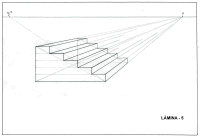
Representaciˇ en perspectiva d'un tram d'escala de cinc graons,
vista de perfil. |
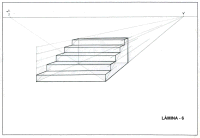
Representaciˇ en perspectiva d'un tram d'escala de cinc graons,
vista frontalment. |
|
L└MINA 7 |
L└MINA 8 |
 |
 |
|
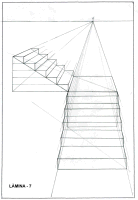
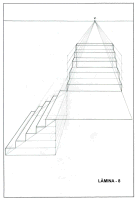
Representaciˇ en perspectiva d'una escala de dos trams en angle
recte, amb el tram de baix vist de front. |
Representaciˇ en perspectiva d'una escala de dos trams en angle
recte, amb el tram de baix vist de perfil. |
| |
|
|
|
| |

|
|
| |
|
|
|
Ě Les corbes en perspectiva: |
|
| |
|
|
| |
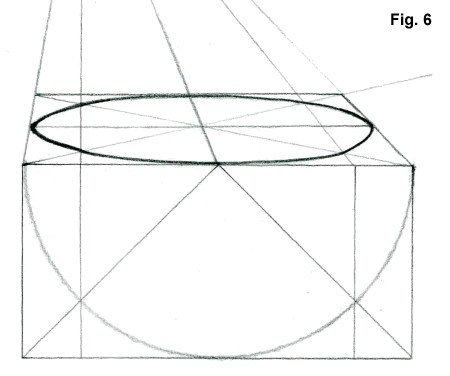
- La CircumferŔncia:
A partir d'una circumferŔncia en disposiciˇ paralĚlela al quadre,
inscrita en un quadrat, projectem cap a V els punts de contacte
de la circumferŔncia amb el quadrat i amb les seves diagonals. Aix˛ ens
servirÓ de referŔncia per al trašat de la circumferŔncia en perspectiva.
Recordem que les mides reals es
transformen visualment en passar a perspectiva.(fig 6)
|
|
| |
 |
|
| |
|
|
| |
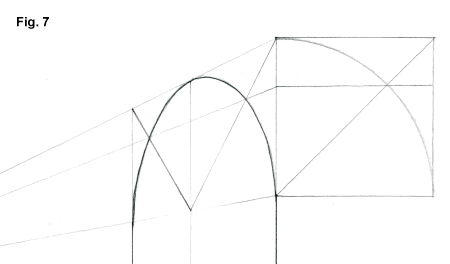
- Els Arcs:
A partir de la meitat de l'arc situat paralĚlel al quadre, es segueix el
mateix procediment que per la projecciˇ de la circumferŔncia cap a V,
projectant els punts de contacte de l'arc amb el quadrant de
circumferŔncia que l'inscriu i la seva diagonal.
Quan projectem un quart de
circumferŔncia obtenim un arc de mig punt, o sigui mitja circumferŔncia.
(fig. 7)
|
|
| |
|
|
| |

|
|
| |
|
|
|
Ě LÓmines amb corbes: |
|
| |
|
|
| |
|
|
| |

|
|
|
Ě Exemples de perspectiva
obliqua: |
|
| |
|
|
| |
|
L└MINA 17 |
L└MINA 18 |
|
(fig. lÓmina 17 )
|
(fig. lÓmina 18 ) |
| |
|
|
L└MINA 19 |
L└MINA 20 |
|
(fig. lÓmina 19 )
|
(fig. lÓmina 20 ) |
| |
|
|
|
| |

|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
 |
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|
| |
|
|