Isometries

• De totes les transformacions que podem tenir en l’espai euclidià, considerarem ací aquelles que conserven el mòdul; aquestes transformacions s’anomenem isometries. De forma equivalent a la definició anterior, es pot veure que les isometries conserven el producte escalar i, en conseqüència, mantenen fixes els valors dels angles i les distàncies.
• Les isometries es poden classificar en dos tipus: les que conserven la orientació de les figures, anomenades congruències, i que, bàsicament, són dues: les translacions i els girs; i les que canvien la orientació de les figures, anomenades anticongruències, que són les simetries central (respecte un punt), axial (respecte una recta) i especular (respecte un pla).

Translació

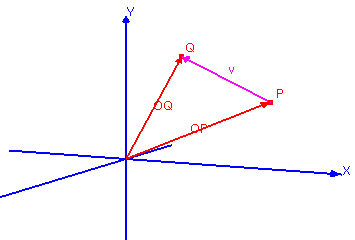
• Una translació es una transformació tal que, donat un vector 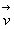, transforma qualsevol punt P en un altre punt Q de forma que el vector 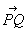és equipol·lent al vector :.

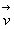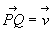L’equació vectorial de la translació és: on és el vector de posició del punt transformat Q i és el vector de posició del punt inicial P.

Exercici 1: Dibuixa amb la el punt P=(7,3,0) i el vector =(-3,2,1). Traslada P segons el vector . Mira les noves components del punt i comprova-les, mentalment, amb l'equació vectorial de la translació. .

Gir Un gir és una transformació tal que, fixada una recta E, anomenada eix del gir i un angle a, a qualsevol punt P li fa correspondre un altre punt Q de manera que: el vector és perpendicular a l’eix E; les distàncies de P i Q a l’eix son iguals; l’angle entre els vectors perpendiculars a l’eix E, que van des d’aquest fins als punts P i Q, és a.(no representat en la figura).

L’equació vectorial d’un gir d’angle a al voltant d’una recta de vector unitari director i que passa pel punt R és:

on és el vector de posició del punt transformat Q i és el vector de posició del punt inicial P.

Exercici 2: Dibuixa amb la el punt P=(0,3,0) i la recta r que passa pel punt Q=(0,0,0) i té de vector director =(1,1,1). Fes girar un angle de 45º P al voltant de r. Quantes rotacions cal fer perquè P torni a coincidir amb el punt inicial? .

Simetria central

La simetria central és una transformació tal que fixat un punt M, anomenat centre de simetria, transforma qualsevol punt P en un altre punt Q de manera que M és el punt mig del segment . L’equació vectorial de la simetria central és: on els tres vectors de l’expressió anterior són els vectors de posició dels punts respectius.

Simetria axial

Tenim una recta r respecte la qual es fa la simetria axial del punt P. Designem per M al punt de la recta que és la projecció ortogonal de P sobre r (M és el punt de r més pròxim a P). El punt Q simètric de P respecte al punt M és el transformat de P segons la simetria axial. Per tant, aquesta simetria es redueix a l’anterior un cop hem trobat el punt M.

• Exercici 3: Dibuixa amb la el punt i la recta de l'exercici anterior, i comprova que fent dues vegades la simetria del punt respecte la recta, aquell es queda igual. Prova-ho, també, al revés, fent la simetria de la recta respecte del punt. .

Simetria especular

Tenim un pla p respecte al qual es fa la simetria especular del punt P. Designem per M al punt del pla que és la projecció ortogonal de P sobre p (M és el punt de p més pròxim a P). El punt Q simètric de P respecte al punt M és el transformat de P segons la simetria especular. Per tant, aquesta simetria es redueix a la simetria central respecte del punt M.