|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Resolució de problemes i més coses sobre triangles |
|
|
|
|
Començarem aquesta pràctica ampliant un poquet temes ja tractats en pràctiques anteriors amb noves comandes aplicables als triangles que ens permetran desenvolupar com a aplicació didàctica la construcció i visualització de la recta d'Euler d'un triangle. Completarem els temes de geometria plana del curs veient com es poden conjecturar amb la Wiris solucions de problemes geomètrics (i també resoldre'ls), amb alguns exemples fets i explicats. |
|
|
|
Punts notables d'un triangle |
|
Dels quatre punts notables d'un triangle que s'estudien a la secundària (ortocentre, baricentre, incentre i circumcentre), tres estan alineats. La recta que els conté s'anomena recta d'Euler. La Wiris ens pot ajudar molt per fer visual el tema i, en concret, en l'exercici 2 d'aquest mòdul se us demana que construïu una pantalla activa de la Wiris per mostrar interactivament els quatre punts notables d'un triangle i la recta d'Euler. En la pràctica 3 vam donar idees per comprovar l'existència del baricentre; tot seguit estudiarem amb detall l'exemple de l'ortocentre i en l'apartat següent trobareu més recursos de la Wiris relacionats amb segments i triangles, que us resultaran d'utilitat per fer l'exercici que hem comentat, si és que opteu perquè sigui un dels que envieu. |
|
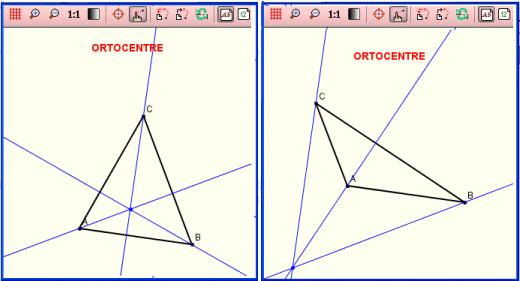
| L'exemple de l'ortocentre | |
|
|
|
|
|
|
|
En la pantalla activa que podeu obrir amb la icona de l'esquerra trobareu l'exemple que dóna lloc a la imatge anterior amb diferents maneres de construir l'ortocentre utilitzant els recursos que incorpora la Wiris. A continuació, es detallen les comandes que s'hi han emprat. |
| Comencem definint i dibuixant un triangle i els seus vèrtexs: | |
 |
|
|
|
|
|
Per trobar l'ortocentre constructivament definirem les rectes que contenen les altures i caldrà resoldre el sistema donat per les seves equacions. Observeu que si resolem el sistema amb les tres equacions a més estem constatant de manera fefaent l'existència de l'ortocentre.
Si voleu repassar els conceptes de llista i de taula, podeu consultar la pràctica 1 del mòdul 2. |
|
 |
|
|
Finalment, establim les propietats del tauler gràfic i dibuixem els elements que falten: les altures i el títol de l'activitat. |
|
 |
|
|
Però la Wiris té recursos que ens estalvien molta feina (perquè ja incorporen la que acabem de fer!) com són les comandes altura i ortocentre. Vegeu-ho tot seguit i comproveu, també, que la intersecció de les tres altures la podríem fer amb la comanda intersecció... |
|
 |
|
| ...i que si només volíem l'ortocentre, encara era més immediat! | |
 |
|
|
|
|
|
|
Més comandes de la Wiris relacionades amb triangles i polígons |
| Tal com ja hem vist
i utilitzat anteriorment, la comanda segment,
icona |
|
|
Pel que fa als triangles ja hem treballat amb algunes comandes. Si pensem en un triangle T com a argument ja hem treballat amb angle(T,i)que per i en 1..3 ens retorna les mesures dels angles. També tenim costat(T, i)que ens retorna les longituds dels costats. I si volem les equacions dels costats d'un triangle T podem fer servir recta(T, i). Aquestes comandes també són aplicables als polígons i a les poligonals. Altres comandes relacionades amb els triangles amb una sintaxi semblant
a l'anterior, que també és la que acabem de veure per altura,
són: mitjana, (allò que de vegades,
incorrectament segons els lingüistes, en diem mediana), mediatriu
i bisectriu. Encara en tenim d'altres que reben com a argument, directament, un triangle: baricentre, circumcentre, incentre, circumradi i inradi. i retornen el que el seu nom indica, un punt o un valor numèric. |
|
|
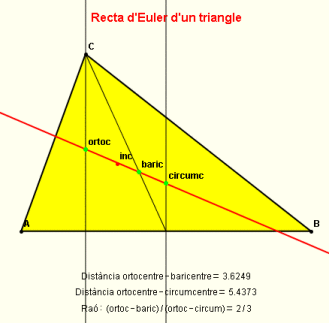
Ara serà el moment de practicar. En l'exercici 2 d'aquest mòdul se us proposa construir un tauler gràfic amb un triangle (que es pugui variar interactivament) que mostri l'ortocentre, el baricentre, l'incentre, el circumcentre i la recta d'Euler del triangle. Opcionalment, podeu fer que aquest tauler també mostri visualment per què el baricentre està dintre el segment determinat pels altres dos punts de la recta d'Euler amb raó de distàncies 2/3. Ho podeu raonar amb la imatge següent (els raonaments no els fa la Wiris!) a partir de la semblança de triangles i la propietat anàloga per al baricentre, el vèrtex i el punt mitjà del costat. |
|
|
|
|
El baricentre es troba entre l'ortocentre i el circumcentre, amb raó de distàncies 2:3 |
|
|
|
Resolució de problemes amb la Wiris |
| La Wiris és una eina important per fer conjectures i resoldre problemes. Vegem un exemple d'aplicació de les comandes estudiades en aquest mòdul per a l'estudi de tres problemes geomètrics: | |
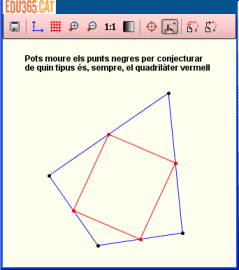
| Problema 1: quadrilàter de punts mitjans | |
 |
|
| En un quadrilàter marquem els punts mitjans dels costats i construim un nou quadrilàter que tingui per vèrtexs aquests punts. De quin tipus és el quadrilàter que hem construït? | |
|
Fem el dibuix amb la Wiris (elpodeu obtenir si cliqueu a la icona de l'esquerra). Naturalment el fem interactiu per poder conjecturar "què passa" amb "qualsevol" quadrilàter inicial. Aquesta és la gràcia de la geometria dinàmica que podem fer amb la Wiris.
|
|
|
Després d'experimentar una estona... heu arribat a alguna conjectura? Ho és sempre, realment? |
|
|
Si voleu fer una comprovació podeu afegir aquestes línies
a la finestra de codi: |
|
| Hem demostrat que el quadrilàter
de punts mitjans és sempre un paral·lelogram? Deixarem la resposta oberta; segur que hi ha opinions diverses. Però del que ningú pot dubtar és de que hem fet una bona feina!!! |
|
|
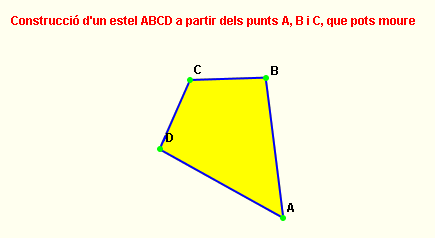
Problema 2: construcció d'un estel ABCD que tingui per
vèrtexs consecutius |
|
|
La figura amb què tot seguit treballarem es defineix així:
És fàcil demostrar una propietat que també caracteritza aquest tipus de quadrilàters:
Veurem la resolució del problema enfocada des d'aquests dos punts de vista i per altra banda també comentarem dues ampliacions del problema.
|
|
|
|
|
|
|
|
|
|
A partir de la definició inicial, per trobar el punt D cal fer una circumferència de centre A i radi AB i una altra circumferència de centre C i radi CB. La intersecció d'aquestes dues circumferències són els dos punts B i D. És molt interessant que intenteu escriure les comandes adequades de la Wiris a partir d'aquestes indicacions i, naturalment, que les completeu amb els comandes per dibuixar el gràfic de manera que sigui interactiu i que si movem els punts A, B o C es trobi la posició de D. La imatge següent mostra la línia fonamental de treball que cal seguir. Fixeu-vos que això mateix seria el que haurien de fer els nostres alumnes i les nostres alumnes de batxillerat en les classes de geometria analítica... però sovint omplirien un full amb moltes equacions sense cap explicació. La Wiris ja fa els càlculs (i, de fet, fa geometria analítica) i llavors, sobretot, ens cal (i també els caldria als nostres alumnes) explicar el procediment i fer geometria. Si voleu confrontar el vostre procediment amb el que us proposem tot seguit, endavant! Potser a l'hora de fer-lo heu tingut algun problema amb la intersecció i la tria del punt que ha de ser D.
Recordeu que de moment no s'imposa que l'estel sigui convex. |
 |
|
|
Ara bé, si en lloc de partir de la definició inicial volem fer servir la propietat característica, el procediment també serà senzill. D serà, simplement el punt simètric de B respecte a la recta AC. Escriviu les comandes a partir d'aquestes indicacions i completeu el dibuix. Segur que haureu trobat l'estel ABCD a partir de A, B i C (que seran, doncs, vèrtexs consecutius de l'estel). Com abans, us proposem tot seguit una solució (de la qual veieu la imatge de les línies principals), encara sense la comprovació que el quadrilàter sigui convex. |
|
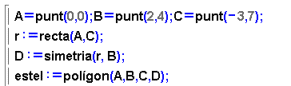 |
|
|
Hem dit que la primera ampliació a aquest problema que hem plantejat seria la d'imposar que ABCD sigui un quadrilàter convex. La comentem tot seguit. Recordeu que estem construint un estel ABCD del qual coneixem tres vèrtexs consecutius. Només que penseu una mica, veureu que si pot fallar que ABCD sigui convex, només pot passar en el vèrtex C o en el vèrtex A, no en el B. Us proposem solventar el problema donant un avís en cas que no ho sigui. I això ho podeu fer afegint les línies següents (i una altra que faci escriure el missatge, és clar!) a la finestra de Wiris on heu escrit la solució a la construcció geomètrica de l'estel. |
|
 |
|
|
Ara bé, el tema d'ampliació més subtil apareix si es vol plantejar el problema d'una manera més general i estudiar en quines condicions, donats tres punts, poden ser vèrtexs d'un estel convex (no cal que siguin consecutius). Si us interessa el tema, cliqueu a la icona de l'esquerra i obrireu una finestra on trobareu un estudi complet i explicat amb tot detall. |
|
|
|
|
| Problema 2: donades tres rectes paral·leles,
construïu un triangle equilàter de manera que tingui un vèrtex sobre cada una de les rectes |
|
|
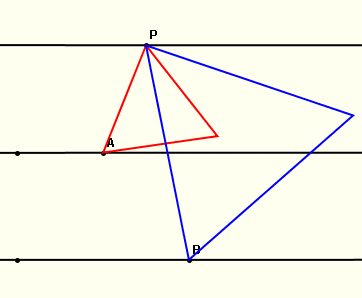
En el problema anterior, era relativament senzill veure com havíem de fer la construcció directament, sabent la definició de quadrilàter estel. Ara en aquest apartat, que podeu considerar absolutametn d'ampliació en una primera passada per la Wiris, ens trobem amb un problema més complex del qual teniu l'enunciat al títol de l'apartat. Per comprendre com l'hem de resoldre, podem fer una primera construcció exploratòria que ens ajudi a entendre la situació. |
|
|
|
|
|
|
|
|
Cliqueu a la icona de l'esquerra per experimentar la situació de les paral·leles i els dos triangles equilàters del dibuix anterior. Observeu que per començar hem rebaixat l'exigència del problema, dibuixant triangles equilàters que tenen només dos vèrtexs sobre paral·leles diferents. Les prestacions de la Wiris ens permeten així buscar empíricament la solució o les solucions del problema i després observar les propietats de la/les solucions per esbrinar com hem de construir la solució del problema. |
| Definim la primera recta, amb un punt P que es mogui sobre ella, amb l'ajut d'un punt auxiliar P1, que no dibuixarem pas: | |
| Definim les rectes segona i tercera, paral·leles a la primera, passant per uns punts P2 i P3 que dibuixarem per poder moure les paral·leles. Definim també uns punts A i B que obliguem a moure's sobre les paral·leles: | |
| Definim els triangles equilàters sobre els costats PA i PB. Aquests triangles tindran només dos vèrtexs sobre paral·leles diferents, però podrem moure'ls per aconseguir que els tres estiguin un sobre cada paral·lela i aleshores observarem la relació que guarden els elements del dibuix quan són solució del problema, i així veurem com hem de fer la construcció de la/les solucions: | |
| Finalment, establim les propietats del tauler i dibuixem els elements geomètrics amb els atributs adients: | |
 |
|
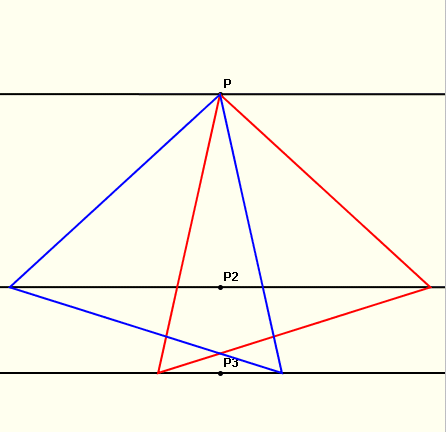
| Solució del problema 2 | |
|
|
|
Solució interactiva al problema de construir
un triangle/s equilàter/s |
|
|
|
Un cop vist el problema, només canviant dues línies de la finestra activa arribem a la solució. Es tracta de construir adequadament els punts A i B de l'activitat exploratòria per obtenir els triangles amb la propietat desitjada. Obriu la finestra activa de l'esquerra per veure'n el resultat. |
 |
|