|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
|
|
Geometria del triangle i els polígons |
|
|
|
|
En la pràctica 6
del mòdul 1 vam veure els elements fonamentals de treball amb
la geometria: les comandes per crear i dibuixar punts, rectes, segments,
triangles, paral·leles, perpendiculars, bisectrius, interseccions,
circumferències i còniques, totes elles disponibles amb
les icones de la carpeta En aquesta pràctica treballarem la geometria del triangle i els polígons, avançant una mica més en la creació de taulers gràfics interactius per manipular conceptes i propietats. Concretament, veurem les comandes necessàries per crear una activitat interactiva que mostri la propietat de la suma dels angles d'un triangle i una altra activitat amb resposta per estimar l'àrea de quadrilàters. En l'exercici 1 es proposa que completeu la primera d'aquestes dues activitats. |
|
|
|
La suma dels angles d'un triangle val 180º |
| Començarem amb una activitat elemental: una propietat molt interessant que sovint els nostres alumnes obliden i que està en la base de molts raonaments geomètrics: | |
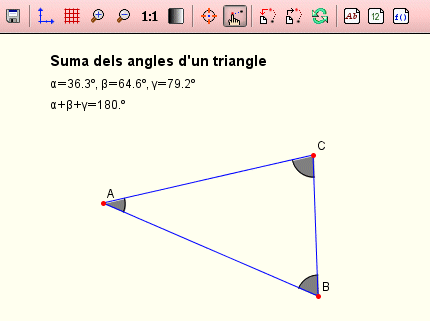
|
|
|
Es poden moure els vèrtexs i totes les dades s'actualitzen interactivament |
|
|
|
Clicant a la icona de l'esquerra podreu veure i executar les comandes
que creen el tauler gràfic interactiu de la imatge anterior. Observeu
que els vèrtexs es poden moure, però, en aquesta primera
presentació a fi i efecte els arcs es mostrin correctament, no
es pot passar cap vèrtex al semiplà contrari respecte a
la recta que conté el costat oposat, és a dir que els vèrtexs
A, B, C del triangle han de trobar-se situats en sentit antihorari. ( A continuació, detallarem les comandes emprades i la seva sintaxi. Podeu intentar reconstruir l'activitat sense obrir la solució que trobareu en la finestra activa de la dreta. |
|
|
Comandes de la Wiris relacionades amb triangles i polígons |
| Primera part: la definició dels objectes geomètrics | |
| Començarem definint
els tres vèrtexs del triangle amb la icona |
|
Tot això és més llarg d'explicar que d'escriure en el tauler interactiu de la Wiris. També és ben fàcil d'entendre un cop ho hem escrit: |
|
 |
|
| Una alternativa per definir els arcs és
fer servir tres punts que els defineixin (centre, punt inicial, punt final). |
|
| A continuació, definim tres capses de text (Text1, Text2, Text3) amb la comanda capsa_de_text que vam veure en la pràctica 1 del mòdul 3. Una capsa de text per cada línia d'informació del tauler gràfic. Recordeu que per concatenar text fix (escrit entre cometes) i variables, s'utilitza el símbol|. Vegeu també que solventem allò del grau_angular posant els símbols º com un text concatenat en la capsa de text corresponent. | |
|
|
|
| A la segona part definim les propietats del tauler gràfic, perquè no es mostri ni el valor, ni els eixos ni la malla. Recordeu la sintaxi de les ordres per modificar el tauler: | |
|
Finalment, a la tercera part escrivim les ordres per dibuixar tots els elements en el tauler gràfic de la Wiris. Adoneu-vos en especial de...
|
|
 |
|
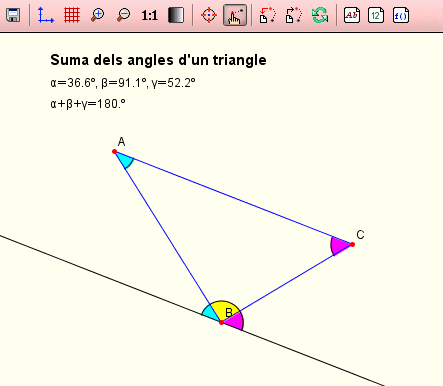
| En l'exercici 1 d'aquest mòdul se us proposa que completeu l'activitat anterior, per mostrar visualment que els tres angles sumen 180º, com en la imatge següent: | |
|
|
|
Podem mostrar visualment i de manera interactiva que la suma val 180º |
|
|
|
Àrea d'un quadrilàter amb resposta interactiva |
| Quina és l'àrea del quadrilàter? La sabríeu encertar amb un marge d'error determinat? I si la Wiris controlés la nostra resposta i ens digués si és correcta o no? La unitat de mesura és el quadrat de la malla. Vegem com construir aquesta activitat didàctica. | |
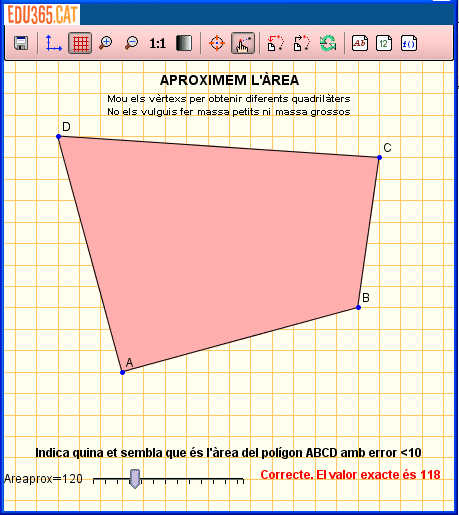
|
|
|
|
|
|
|
A continuació, detallarem les comandes emprades i la seva sintaxi. Com a activitat d'ampliació, podeu intentar reconstruir l'activitat sense obrir la solució que trobareu al final de les explicacions. Si només voleu veure com funciona l'activitat, sense mirar el codi, podeu obrir el tauler gràfic amb el codi amagat. Si ho voleu fer amb alumnes potser els direu: comenceu per un rectangle, després un paral·lelogram... |
|
|
Comandes emprades en la creació de l'activitat anterior |
| Per a aquesta activitat, que és una mica més complexa que l'anterior, desglossarem la primera part en diferents apartats i comentarem les comandes noves amb més detall. Un cop d'ull a les imatges donaran aquella comprensió global que amb les paraules és més difícil d'assolir: | |

|
|
|
La comanda polígon genera el polígon resultant d'unir els vèrtexs de la figura, els quals s'entren com a arguments de la funció. Es dibuixen ordenadament els segments entre els vèrtexs indicats i el darrer vèrtex entrat com a argument s'uneix amb el primer per tancar el polígon.
|
|
| La comanda àrea calcula l'àrea de la figura que rep com a argument, suposant que sigui tancada (triangle, polígon, circumferència o el·lipse). | |
| S'ha triat un recorregut perr al desplaçador que sembla adequat, però es pot canviar sense cap problema. Més avall ja es fa dibuixar el depslaçadaor a la part inferior esquerra de la pantalla i es guarda, com veureu, la part inferior dreta per a la resposta d ela Wiris. | |
 |
|
|
Construïm la resposta de la Wiris emprant una mica de programació:
la sentència
|
|
| Per acabar, quan ja ho tenim tot definit, donem les instruccions de dibuix i escriptura. | |
 |
|
|
|
Cal remarcar que l'ordre en que es donen aquestes comandes de dibuix
i escriptura no ha estat pas escollit a l'atzar: observeu que es dibuixa
el polígon i els vèrtexs en primer lloc per aconseguir mantenir
el polígon en segon pla, perquè no oculti les instruccions
i les respostes en cas d'estirar-lo a una mida prou gran. Per veure tot el codi que ha servit per elaborar l'activitat, podeu obrir una finestra activa de la Wiris clicant a la icona de l'esquerra.
|
|
|
|
|
Si ja heu enllestit la pràctica i ja heu conegut treballat amb la comanda àrea pot ser interessant comentar com podríem solventar el problema que tenim en la primera activitat d'aquest apràctica de no poder moure lliurement els punts del triangle perquè, segons com els movem els arcs passen a marcar els angles exteriors i no els angles del triangle (en canvi la comanda triangle(T,i) sempre dóna, com heu vist, els angles del triangle). L'artifici serà presentar la comanda àrea_orientada que, aplicada a un triangle o un polígon ens dóna resultat positiu si els vèrtexs que defineixen el triangle estan situats en sentit antihorari (com a l'exempledel triangle tal com s'ha trebalat ) i en canvi dóna negatiu si els vèrtexs estan situats en sentit horari. Aleshores es tractarà de definir uns arcs
o uns altres condicionats pel valor de àrea_orientada(T).
Si ho fem així, quan dibuixem Arcs tot funcionarà! |
|