|
|
||||||||||||||||
 |
||||||||||||||||
 |
Pràctica |
 |
 |
 |
 |
 |
|
|
Exercicis
|
 |
||||||
|
|
Geometria constructiva versus geometria analítica |
|
|
|
| És clar que sempre que fem geometria amb la Wiris (o amb el Cabri, la Cinderella...), al darrere hi ha la geometria analítica. La pantalla de treball de la Wiris ens permet visualitzar les equacions, però, alhora, ens obliga a un procés constructiu i ens permet posar l'èmfasi més en el problema que no en les eines per resoldre'l. D'aquesta manera, desapareix el fals dilema ¿geometria constructiva o geometria analítica? i se li dóna l'única resposta interessant: Geometria. | |
|
En aquesta pràctica veurem com la Wiris integra els dos mètodes de treball habituals en la geometria: el mètode constructiu i el mètode analític. Començarem amb una explicació detallada de la comanda intersecció que naturalment serà un element de treball fonamental per resoldre problemes, cosa que quedarà palesa en els exemples que mostrarem.
|
|
|
Escriptura i sintaxi de la comanda Intersecció |
|
|
La sintaxi de la comanda per obtenir la intersecció té dues possibilitats:
Ara convé indicar un aspecte fonamental. Tot i que en la darrera pràctica d'aquest mòdul comentarem la manera de donar una recta de l'espai com a intersecció de dos plans...
Vegeu dos exemples que il·lustren això que acabem de comentar. En el primer exemple noteu que podem dibuixar els quatre punts d'intersecció, "globalment", com una llista. Però, en canvi
En aquest segon exemple adoneu-vos que amb el símbol
|
|
|
Posició relativa recta-circumferència |
|
Presentem tot seguit una activitat que reforçarà le sidees sobre la comanda que acabem d'explicar. Es tracta d'estudiar la posició relativa recta-circumferència. Una manera de fer-ho és calcular els punts de tall mitjançant la comanda intersecció i comptar quants n'hi ha. Sembla senzill, però ens trobarem amb un petit inconvenient: quan la recta és tangent, el punt de tall és doble, i la llista també té dos elements, però repetits. Per poder distingir bé aquest cas, farem servir la comanda conjunt per eliminar repeticions. |
|
| La imatge següent mostra com ho podem fer, a partir de la comanda intersecció, que ja sabeu que ens dóna els punts de tall en forma de llista, per poder guardar cada punt de tall de manera individual. Vegeu també que a partir d'uns punts inicials posats arbitràriament, definim la recta i la circumferència amb := per poder actualitzar la resposta de la Wiris. | |
 |
|
|
Si escriviu el codi anterior i experimenteu veureu que, fent-ho així, la Wiris no distingeix les posicions secant i tangent. Modifiqueu els punts inicials fins que tingueu una posició en que la recta és tangent a la circumferència i vegeu com es dóna la llista de punts d'intersecció. Tot seguit solucionem el problema introduint la comanda conjunt, que aplicada a una llista la retorna sense elements repetits. Teniu posat un cas d etangència i podue veure que n (nombre de punts d'intersecció) ja val 1. |
|
 |
|
|
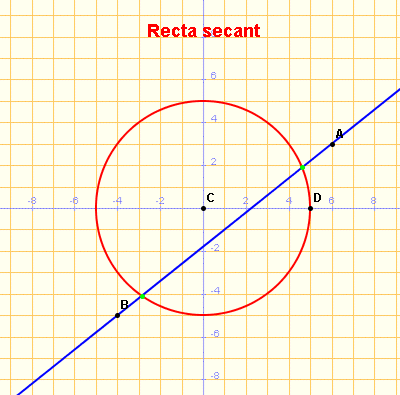
Abans de clicar a la icona de l'esquerra per poder obrir una finestra activa amb una proposta de solució de l'activitat plantejada serà molt interessant que l'intenteu fer sense més ajuda que la imatge que us mostrem seguidament. L'objectiu és aconseguir un tauler gràfic que respongui donant la posició relativa de la recta i la circumferència. Podem escollir la posició dels punts A, B, C i D i la circumferència i la recta s'actualitzen: la circumferència té centre en C i passa per D i la recta passa per A i B. |
|
|
|
|
|
|
|
Construcció d'un paral·lelogram
coneguts tres vèrtexs i punt mitjà de les diagonals. Dos blocs d'instruccions diferents per resoldre el mateix problema |
| En la pràctica 6 del mòdul 1 vam veure el problema de trobar el quart vèrtex D d'un paral·lelogram, donats tres vèrtex A, B i C. Tot i que es començava exposant un mètode vectorial, ja es va comentar que no era la única manera de resoldre el problema. | |
|
|
Ara podeu recuperar les dues maneres: podeu fer clic a la icona de l'esquerra per veure i executar els dos blocs de comandes en una finestra activa de la Wiris on ja hi teniu incloses, a més les comandes de dibuix. Aleshores, penseu primer de tot com continuaríeu l'activitat amb la comprovació que el punt on es tallen les diagonals del paral·lelogram és el punt mitjà dels punts A i C i també dels punts B i D. Després de pensar-ho una estona podeu llegir els comentaris que fem tot seguit sobre el doble camí de solució. |
| (Versió 1) Recordem l'enfocament vectorial: | |
 |
|
|
Com podríem comprovar amb aquesta idea, sense molts més càlculs, que les diagonals es tallen en el seu punt mitjà? Sabem que el punt mitjà de A i C pertany a la diagonal
AC; igualment el punt mitjà de B i D pertany
a la diagonal BD. Si veiem que aquests dos punts coincideixen quedarà
demostrat que és el punt d'intersecció de les dues diagonals.
Per al càlcul directe podeu fer-ho com s'indica seguidament, amb
el benentès que si voleu traslladar-ho a un gràfic interactiu
caldria definir els elements amb
|
|
|
|
|
| (Versió 2) En aquest segon enfocament seguim fil per randa les idees constructives,... però les duem a terme amb els recursos analítics, fent servir l'equació de la recta. | |
 |
|
|
En la imatge anterior només hi falten les ordres per dibuixar
el tauler gràfic que teniu a la finestra activa que heu pogut obrir.
Recordeu les icones per entrar les comandes punt,
recta, paral·lela...
es poden trobar a la carpeta Observeu també que ja hem "convertit" la intersecció de les dues rectes (que estrictament és una llista d'un punt) en un punt. De fet es pot dibuixar DD (i en aquest cas "sembla" que sigui un punt) però no haguéssim pogut fer-hi res més, ni dibuixar els segments que configuren el paral·lelogram, ni escriure l'equació de les diagonals... |
|
Ara podem construir o escriure les equacions
de les dues diagonals (digueu-ho com vulgueu; que amb la Wiris ho farem
alhora), buscar el punt d'intersecció i comprovar que és el
punt mitjà. Com hem fet en la presentació afí, vectorial,
ara ho escrivim per veure el resultat dels càlculs. Com ja hem dit
allà, per a un gràfic interactiu ens caldria fer servir  .
|
|
 |
|
|
|
|
|
Una reflexió final a aquesta pràctica. Sovint es diu com una "pseudocrítica" a la Wiris que és pesat perquè obliga a escriure-ho tot. Però...
Aleshores, quan queden més clares les idees per a la primera part del problema que estudiem (determinar el quart vèrtex d'un paral·lelogram)...
 |
|
 |
|
|
|
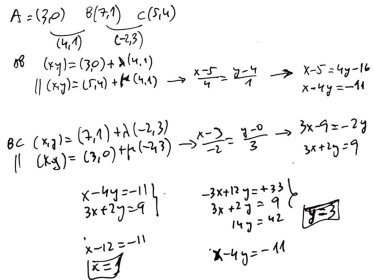de la carpeta Geometria (escriu amb una sintaxi que també
podeu entrar pel teclat; també és vàlida, en comptes
de la comanda 
que
no podeu entrar pel teclat):
,
que la icona 
i que l'assignació 