En aquesta pràctica resoldreu qüestions de probabilitat relacionades amb la distribució de Poisson i la distribució geomètrica. Concretament treballareu:

• La fórmula POISSON que permet la resolució de problemes directes de càlcul de probabilitats que corresponen al model donat per la distribució de Poisson.
• L'elaboració de la taula de la distribució de Poisson.
• La construcció d'una taula de probabilitats de la distribució geomètrica i el seu ús per a la resolució de problemes.

En una editorial no treballen de manera gaire acurada i hem pogut observar que, de mitjana, s'observen 0,66 errades tipogràfiques en cada pàgina de les seves publicacions.

1. Quina és la probabilitat que en una pàgina no hi hagi cap errada?
2. Quina és la probabilitat que en una pàgina hi hagi dues errades o més?
3. Quantes errades trobarem, per terme mitjà, en 10 pàgines de text consecutives d'un llibre d'aquesta editorial?
4. Si els editors volen obrir un dels seus llibres per una pàgina a l'atzar i tenir una probabilitat d'encertar superior al 99 %, si fan una afirmació del tipus "No trobareu més de n errades en aquesta pàgina", quin ha de ser el valor de n? (Amb el benentès que, naturalment, voldran dir el valor més petit possible per a n.)

Molt poca probabilitat d'error en cada lletra.
Moltes lletres en cada pàgina.
Cas límit d'una binomial amb n molt gran i no conegut.
Mitjana d'errades de valor fix, conegut, quan s'analitzen les diverses publicacions d'aquesta editorial.

1. Per resoldre aquest apartat, calcularem, directament, la probabilitat de 0 errades. Podeu fer Insertar | Función | POISSON posant a x 0, a Media 0,66 i a Acumulado 0 o Falso. O bé podeu escriure directament la fórmula = POISSON( 0; 0,66; FALSO).
   Podeu veure que la resposta és 0,517(arrodonint).

2. Heu de calcular la probabilitat acumulada de l'1 (probabilitat de 0 o 1 errades) i restar-la de la unitat. Ho podem fer amb la fórmula = 1-POISSON(1; 0,66; VERDADERO). Resposta: 0,142.

3. Aquesta qüestió no es resol amb un programa informàtic, sinó amb una propietat de la mitjana. La mitjana de la suma d'unes variables aleatòries independents és la suma de les respectives mitjanes. Per tant, la resposta és 0,66 · 10 = 6,6.

4. Per a la recerca del valor crític que es demana en aquest cas, ens aniria bé una fórmula de l'estil de POISSON.CRIT, però no la tenim a la nostra disposició. Hem de buscar els valors de les successives probabilitats acumulades fins que en trobem una superior a 0,99. Podem veure que POISSON( 2; 0,66; VERDADERO) = 0,971 i que POISSON( 3; 0,66; VERDADERO) = 0,995. Per tant, el millor anunci que poden fer els editors és "No trobareu més de 3 errades en aquesta pàgina"; com que aquest anunci vol dir que en trobaran 0, 1, 2 o 3, té una probabilitat d'encert superior al 99 %. Amb menys errades no s'arribaria al mínim risc d'error exigit (l'1 %) perquè l'anunci sigui fiable.

En aquesta part de la pràctica, revisarem el que ja vam fer amb la distribució binomial i així obtindrem una taula que doni tots els valors significatius de la probabilitat per a una distribució de Poisson.

Constatareu algunes diferències amb aquell cas. En primer lloc, ja sabeu que la distribució de Poisson només té un paràmetre que la defineix, la mitjana, sovint designada com a l, i, per altra banda, pot prendre (teòricament) qualsevol valor, però ja sabeu que les probabilitats baixen ràpidament. Tanmateix, a la columna dels valors podem posar-hi tots els nombres que vulguem i no cal escriure cap fórmula condicional.

• Obriu el llibre de l'Excel DISTRIBUCIONS-DISCRETES.XLS que ja teniu preparat amb aquesta finalitat. Accediu al full Poisson.
• A la cel·la A1 escriviu Mitjana i, per enllaçar de moment amb la part anterior de la pràctica, escriviu 0,66 a la cel·la A2.
• A la cel·la B1 escriviu el rètol Valor i ompliu les cel·les d'aquesta columna amb els possibles valors a observar. No oblideu que el 0 és un possible valor de la distribució de Poisson i sigueu conscients que si poseu fins al 100, n'hi ha més que suficient. Recordeu la possibilitat d'escriure aquests nombres correlatius per arrossegament o amb Edición | Rellenar | Series. Si ho voleu fer d'aquesta manera, només cal que escriviu el 0 a la cel·la B2 i que llavors, amb la cel·la B2 seleccionada, activeu el procediment esmentat i indiqueu que voleu les dades en columnes, amb un increment de l'1, Tipo Lineal i límit 100.
• A la cel·la C1 escriviu el rètol Probabilitat i a la cel·la C2 escriviu (a mà o amb Insertar | Función) la fórmula que dóna la probabilitat =POISSON(B2;$A$2;0). Copieu aquesta fórmula perquè sigui vàlida en tot el rang C2:C102.
• A D1 escriviu Prob. acu. i llavors a la cel·la D2 escriviu la fórmula =POISSON(B2;$A$2;1) (anàloga a l'anterior però amb probabilitat acumulada) i copieu-la en tot el rang D3:D102.
• Ja teniu la taula feta! Modifiqueu alguns aspectes de presentació si ho creieu convenient.
• Guardeu el llibre, perquè el necessitareu per a una pràctica posterior.

Observeu en aquesta taula les respostes als diversos apartats del problema plantejat a la primera part de la pràctica.

Tot seguit, modificareu el valor de la mitjana i veureu com s'actualitza la taula, i podreu resoldre l'exercici següent:

En una població amb moltes zones blaves han observat que, de mitjana, cada dia s'espatllen 6 màquines de vendre els tiquets d'aparcament.

1. Quina és la probabilitat que un dia s'espatllin exactament 5 màquines?
2. Quina és la probabilitat que un dia s'espatllin 3 màquines o menys?
3. Quina és la probabilitat que un dia s'espatllin més de 8 màquines?
4. Quina és la probabilitat que un dia s'espatllin entre 6 i 10 parquímetres (inclosos el 6 i el 10)?
5. Quina és la capacitat de reparació de màquines per dia de què s'ha de disposar si es vol que el 80 % dels dies es puguin reparar el mateix dia tots els parquímetres espatllats?
6. I si es vol que això passi el 95 % dels dies?

Poseu a la taula de la distribució binomial la mitjana igual a 6 i llavors les respostes les trobareu a:

1. Cel·la C7.
2. Cel·la D5.
3. Cal restar de la unitat el valor de D10.
4. D12 - D7 o bé la suma del rang C8:C12 (que podeu veure dinàmicament a la part inferior de la pantalla).
5. Heu de baixar per la columna de la Prob. acu fins que el valor observat de la probabilitat acumulada sigui superior al 80 %. Això succeeix a la cel·la D10. Mireu a la columna B i veureu que necessiteu poder reparar 8 parquímetres/dia.
6. Per assolir el 95 %, necessiteu poder reparar 10 parquímetres cada dia.

Quines de les qüestions anteriors es podrien resoldre amb la funció POISSON? Penseu-ho i penseu també com ho faríeu i valoreu quin procediment és més eficaç: l'ús de la fórmula o l'anàlisi global de la taula.

Si cliqueu a la icona de l'esquerra, trobareu el suggeriment d'una interessant simulació que amplia el tema tractat en aquest exercici i permet valorar quina previsió seria més encertada en l'àmbit de les dues darreres qüestions. El 80 %? El 95 %? S'hauria d'arribar al 100 %, o amb menys del 80 % potser ja n'hi hauria prou per atendre raonablement el servei?

En el document de fonaments teòrics s'ha descrit la distribució geomètrica, que fa el recompte del nombre de repeticions independents que cal fer d'una experiència de Bernouilli fins que s'observa el primer èxit.

El programa Excel no inclou la distribució geomètrica entre les seves opcions de treball ni s'hi pot aplicar cap de les fórmules estadístiques.

Incloem en aquesta part de la pràctica l'elaboració de la taula de probabilitats i de probabilitats acumulades de la distribució geomètrica i les aplicarem tot seguit per la resolució d'un exemple pràctic.

• Obriu el llibre DISTRIBUCIONS-DISCRETES.XLS i accediu al full Geomètrica. Construireu la taula de forma ben anàloga al que ja heu fet per a la distribució binomial i per a la de Poisson.
• A la cel·la A1 escriviu-hi el rètol Prob. èxit i a la cel·la A2 el valor de la mitjana de la distribució geomètrica per al primer exemple que fareu. Imagineu que serà per a l'esdeveniment de treure un 6 quan es tira un dau perfecte. Poseu a A2, doncs, =1/6. Després ja variareu aquest valor i s'actualitzarà la taula.
• Per a la descripció del model, poseu a A3 Mitjana i a A4 el seu valor, que s'expressa amb la fórmula = 1/A2.
• A les cel·les B1, C1 i D1 podeu posar els títols Valor, Probabilitat, Prob.acum.
• Al rang B2:B31 escriviu-hi els nombres de l'1 al 30 (ja sabeu que hi ha diverses maneres de fer-ho; adoneu-vos que amb la nostra presentació de la distribució geomètrica el valor 0 no es pot observar).
• Per calcular les probabilitats:
  • A la cel·la C2 escriviu-hi la fórmula =A2 perquè A2 és la probabilitat p d'èxit i la probabilitat d'assolir èxit en laprimera repetició és, doncs, p.
  • A la cel·la C3 escriviu la fórmula C2*(1-A$2) perquè de cada probabilitat es passa a la següent multiplicant per 1 – p.
  • Copieu per arrossegament la fórmula anterior a les altres caselles de la columna que us interessen, és a dir, al rang C4:C31.
• Per calcular les probabilitats acumulades:
  • A la cel·la D2 escriviu-hi la fórmula =C2.
  • A la cel·la D3 escriviu-hi la fórmula =D2+C3.
  • Copieu per arrossegament la fórmula anterior a les altres caselles de la columna D que us interessen.
• Adoneu-vos que ja teniu la taula de la distribució geomètrica i, en particular, constateu que les probabilitats disminueixen molt ràpidament.
• Guardeu el llibre DISTRIBUCIONS-DISCRETES.XLS perquè el necessitareu per elaborar els gràfics de la distribució geomètrica.

Ara aplicarem la taula que teniu al full Geomètrica per a la resolució d'un exemple: suposem que en un municipi (exemple de la pràctica anterior), on el 45 % de la població és favorable a la gestió de l'alcalde, es fa una successió d'entrevistes, independents l'una de l'altra.

1. Quina és la probabilitat que la primera persona que contesti a favor de l'alcalde sigui exactament la quarta entrevistada?
2. Si només podem fer un màxim de 6 entrevistes, quina és la probabilitat que trobem alguna persona que contesti a favor de l'alcalde?
3. Quantes entrevistes hem de fer perquè la probabilitat de trobar una persona favorable sigui superior al 99 %?

La distribució geomètrica és l'adequada a l'exemple; com que p=0,45 és la probabilitat d'èxit en una entrevista, aquest és el valor que cal posar a la cel·la A2. Veureu de seguida que la mitjana del nombre d'entrevistes que cal fer per trobar una persona favorable a l'ajuntament és 1/0,45 = 2,22.

L'anàlisi de les tres columnes que s'han emplenat al full de càlcul us perme esbrinar les respostes al problema plantejat (recordeu que la segona columna dóna els valors, la tercera, les probabilitats i la quarta, les probabilitats acumulades).

1. Mireu la cel·la C5.
2. Mireu la cel·la D7.
3. Si busqueu a la columna D quin és el primer valor que ultrapassa 0,99 el veureu a la cel·la D9, que correspon a 8 entrevistes.

Aquesta taula actualitzable que heu elaborat us pot servir per a un dels exercicis del final del mòdul.

Aquest comentari d'ampliació està suggerit pel vídeo L'atzar de la sèrie de programes d'estadística de la BBC que en el seu moment (en dues ocasions) va emetre TV3. És ben cert que aquests programes tenen una presentació antiquada, però, tanmateix, el cúmul d'idees que se'n poden treure és molt interessant.

Hem vist a la pràctica que si disposàveu de la capacitat de reparar 8 parquímetres/dia, llavors el 80 % dels dies ja donàveu abast. Ara ens podem plantejar la qüestió següent: el que s'ha dit és cert, però podria passar que l'acumulació de feina no resolta el 20 % dels dies restants arribés a col·lapsar el servei? Si això fos així, caldria pensar a disposar de 9 reparacions/dia. O, en canvi, si només reparéssim un màxim de 7 parquímetres, ja seria una xifra raonable?

Una simulació ens ajudarà a respondre aquestes preguntes:

• Inseriu un full nou al llibre DISTRIBUCIONS-DISCRETES.XLS i anomeneu-lo Reparacions. A la cel·la A1 escriviu Reparacions i a la cel·la A2 escriviu 8.
• A la cel·la B1 escriviu Simulació i a la cel·la C1, Feina pendent.
• Activeu Herramientas | Análisis de datos | Generación de números aleatorios i ompliu així el quadre de diàleg corresponent:
  
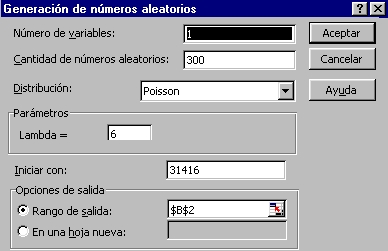
  Amb això simulem quants parquímetres s'espatllen cada dia durant 300 dies seguits. L'opció Iniciar con té com a finalitat assegurar que en diferents ordinadors aparegui la mateixa simulació; feu-ho servir o no, com us sembli.
• A la columna C farem el compte del nombre de parquímetres que queden per reparar al final de cada jornada.
  • Si el nombre de parquímetres espatllats aquell dia més el nombre dels que quedaven del dia anterior és més petit o igual que 8, cal que poseu un 0 a la cel·la corresponent.
  • Altrament, heu de posar-hi el resultat de restar 8 a la suma del nombre de parquímetres espatllats aquell dia més els que quedaven del dia anterior.
  Escriviu, doncs, les fórmules següents:
  • A la cel·la C2, =SI(B2<=$A$2; 0; B2-$A$2).
  • A la cel·la C3, =SI(B3+C2<=$A$2; 0; B3+C2-$A$2).
  • Copieu aquesta darrera fórmula a tot el rang C4:C300.

• Penseu que la mitjana de parquímetres espatllats és de 6, i que el valor 8 l'heu triat perquè un 80 % dels dies assegureu que podeu reparar totes les avaries; en aquestes condicions, analitzeu què passa amb 8 reparacions per dia. En totes les simulacions que hem fet els autors (inclosa la que us proposem amb Iniciar con 31416), hem pogut veure que, tot i que en algun període excepcional s'ha acumulat la feina i durant uns dies hi ha hagut parquímetres fora de servei, ben aviat s'ha normalitzat.
• Torneu a activar el procediment per fer la simulació (amb un altre nombre enter a Iniciar con si heu fet servir aquesta opció) copiant les dades a sobre de les anteriors, i valoreu-ho novament.
• Si algú pensa que tenint contractada una capacitat de reparació igual al nombre de parquímetres que s'espatllen cada dia de mitjana ja n'hi hauria prou, que posi un 6 a la cel·la A2, que faci la simulació i veurà que no és pas així. I si té dubtes, que repeteixi la simulació! D'aquesta manera, la feina no aniria endavant!
• I si fixem que es poden reparar 7 parquímetres/dia, com valoreu els resultats?