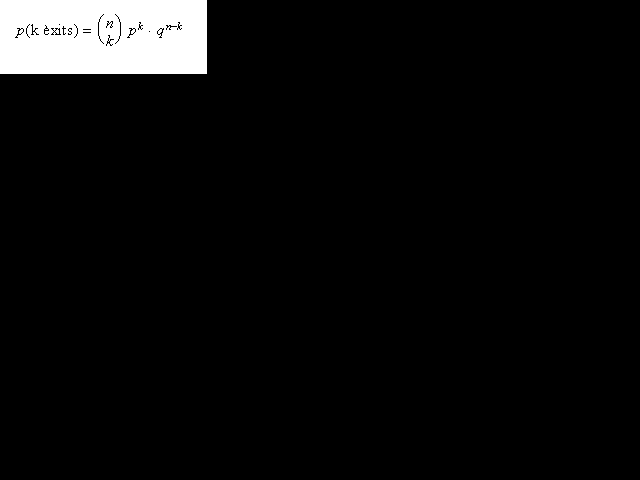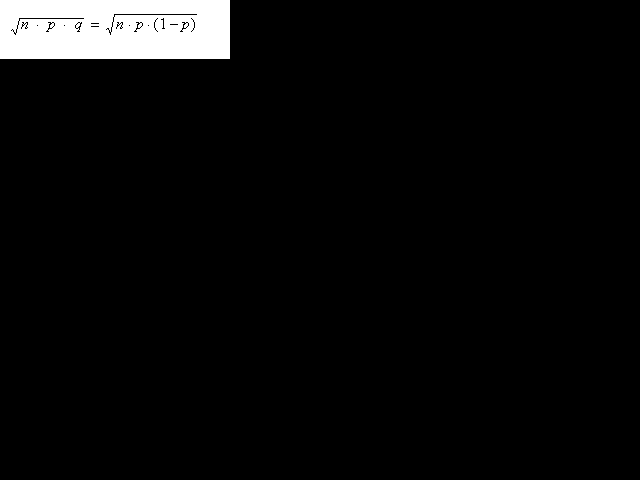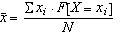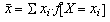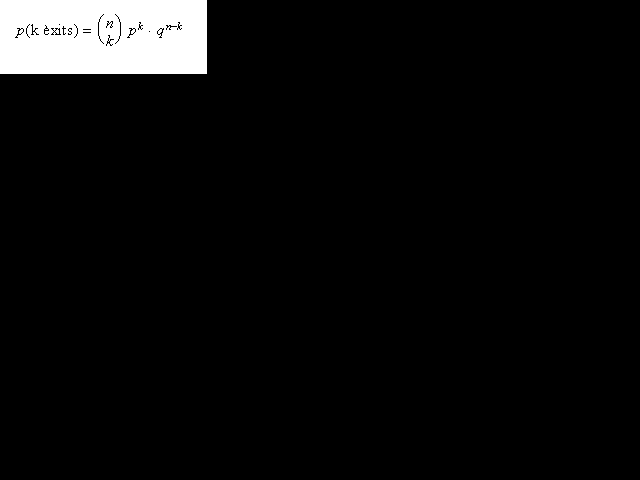|
|
Les distribucions de probabilitat discretes 
En aquest document s'introdueix la idea de variable
aleatòria, es comenten les diferències entre les
de tipus discret i les contínues i es presenten les
principals distribucions de probabilitat discretes. També
s'explica quines són les situacions pràctiques que
modelitzen.

Amb aquesta idea definim una variable aleatòria
|
|
|
Variables aleatòries discretes i
contínues
En la realització d'una experiència
aleatòria sovint ens interessa representar els diferents
resultats que podem observar mitjançant nombres. Per
exemple:
- Quan tirem un dau enlaire sovint indiquem les cares com {1,
2, 3, 4, 5, 6} tot i que els símbols que marquen
són uns altres.
- Si fem l'experiència de tirar enlaire 5 monedes i comptar el nombre de cares que surten, diverses
posicions de les monedes ens porten a dir "2", unes altres "4", etc.
- Quan triem a l'atzar una noia d'una classe podem mesurar-ne
l'alçada, o el pes, o preguntar-li quants anys té.
El valor obtingut d'aquestes variables es representa
també mitjançant nombres.
- Quan observem el resultat d'una travessa el que ens
interessarà serà "traduir" la columna amb 1, X i 2
a "nombre d'encerts" primer de tot i si escau a "guanys".
Tots aquests són exemples de variables aleatòries.
Es diu que hem associat una variable
aleatòria a un experiment aleatori quan representem
cada possible resultat mitjançant un nombre.
Segons quin sigui el conjunt de possibles resultats
numèrics que podem observar, les variables
aleatòries es classifiquen en
- variables aleatòries discretes,
caracteritzades perquè els valors que poden prendre
són els elements d'un conjunt finit o infinit numerable.
- variables aleatòries contínues per a
les quals els valors que podem observar són,
conceptualment, elements qualssevol d'un interval de nombres
reals.
Podem dir que si fem moltes repeticions d'una experiència
que tingui associada una variable aleatòria discreta i
fem el recompte dels resultats numèrics que observem ens
trobem amb una variable estadística discreta. En
són exemples: el resultat observat quan tirem un dau; el
nombre de creus que comptem si tirem cinc monedes enlaire; el
nombre d'encerts en una travessa...
Anàlogament, el recompte dels resultats observats en
moltes repeticions d'una experiència que té
associada una variable aleatòria contínua ens
portaria a una variable estadística contínua. En
són exemples: la mesura de l'alçada d'una noia
escollida a l'atzar en una classe; el temps que dura una pila
elèctrica...
L'estudi de les variables aleatòries ha d'anar acompanyat
de la consideració del càlcul de les probabilitats
dels esdeveniments considerats i llavors, per a cada nombre real
a, hom pot considerar diverses probabilitats que
ajuden a caracteritzar el model.
En primer lloc cal considerar:
p[X=a], que representa la probabilitat del
conjunt format per tots els casos possibles de
l'experiència que donen com a resultat a.
La consideració dels valors de les probabilitats p[X=a] diferencia molt clarament les variables discretes de les contínues. Per
exemple:
- Per a la variable X associada al nombre que marca un
dau, si suposem vàlid el model uniforme (dau ben
equilibrat), serà
p[X=1] =
p[X=2] = ... = p[X=6] = 1/6
p[X=a] = 0 si a no és de {1, 2, 3, 4, 5, 6}
- Per a la variable X, associada al nombre de creus que
observem si tirem cinc monedes enlaire tindrem únicament
sis valors diferents de 0, els que corresponen a aquestes probabilitats:
p[X=0], p[X=1],... i
p[X=5]
p[X=a] = 0 si a no és de {0, 1, 2, 3, 4, 5}.
- En canvi, per a la variable X associada a
l'alçada d'una noia serà
p[X
exactament = 1,70] = 0, de la mateixa manera que
p[X=1,69876543] = 0. No podem observar "amb
exactitud" els valors d'una variable contínua. En aquest
cas 1,7000000 o bé 1,69876543 no són
observables, com ja s'ha comentat al document
d'introducció a la
probabilitat.
Per a l'estudi de les variables discretes (i encara molt més per a les contínues) serà un
element fonamental la consideració de
p[X
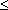 a], que representa la
probabilitat del conjunt format per tots els casos possibles de
l'experiència que donen com a resultat per a la variable aleatòria un valor menor o
igual que a. Aquestes probabilitats es poden considerar per qualsevol nombre
a. a], que representa la
probabilitat del conjunt format per tots els casos possibles de
l'experiència que donen com a resultat per a la variable aleatòria un valor menor o
igual que a. Aquestes probabilitats es poden considerar per qualsevol nombre
a.
En la recerca d'un model per a una situació
empírica deixa de ser fonamental l'estudi de la variable
aleatòria i esdevé crucial la consideració
de les probabilitats. És per això que es parla
sovint de distribucions de probabilitat molt més
que de la pròpia variable aleatòria. Hem
d'entendre amb aquesta denominació tot el conjunt dels
elements que s'empren en l'estudi de les variables
aleatòries.
|
|
|
Estudi de les distribucions de probabilitat discretes
 |
S'anomena funció de probabilitat associada a
una variable aleatòria discreta X,
la funció f que a cada nombre real x li
assigna la seva probabilitat: f(x) =
p[X=x].
|
La funció de probabilitat f d'una variable
aleatòria discreta es caracteritza per:
- f(a) és sempre positiu o zero.
- Només hi haurà una col·lecció ben
determinada de valors x1,
x2, x3,...
,xn,... per als quals la funció de
probabilitat donarà valor diferent de zero.
- Es compleix que la suma de les probabilitats de tots els
valors que poden observar-se com a resultat de
l'experiència és 1. Aquesta propietat fa que la
funció de probabilitat es conegui també amb el nom
de funció de masses. La "probabilitat total" (la
unitat) entesa com una massa es reparteix entre uns quants punts
aïllats "que pesen". En tots els altres punts o nombres
reals no hi ha "massa de probabilitat" (no poden esdevenir-se
com a resultat de l'experiència).
Si volem fer una representació gràfica de la
funció de probabilitat o funció de masses d'una
variable aleatòria discreta convindrà que fem del
tot evident el seu caràcter discret, discontinu.
És per això que es recomana elaborar un diagrama
de barres en què graduarem l'eix vertical segons els
valors de les probabilitats. En alguns textos aquest diagrama
és anomenat (pensem que erròniament) histograma de
probabilitats.
Les funcions d'Excel s'apliquen directament per a treballar
amb les distribucions de probabilitat sobretot des del punt de vista numèric;
aquest aspecte es treballa en les quatre primeres pràctiques. Per obtenir-ne
una visió gràfica, podeu estudiar la pràctica 5 d'aquest mòdul.
El primer exemple que convé
presentar és el model de què ja hem parlat quan s'ha
estudiat la fórmula de Laplace, aquell que representa una
experiència aleatòria amb un nombre finit de casos
possibles, tots igualment probables. L'Excel no hi fa una
referència especial sinó que s'ha de construir "a
mà" i aplicar-hi les construccions dels que s'anomena distribució discreta.
 |
La distribució uniforme discreta correspon a
una variable aleatòria associada
a una experiència simple a partir de la qual es poden obtenir n resultats numèrics, representats habitualment amb els nombres {1,
2, 3, ..., n}, que tenen tots la mateixa probabilitat.
|
Per a la distribució uniforme discreta:
- p[X=i] = 1/n, si i pertany al conjunt
de possibles resultats.
- p[X=a] = 0, altrament.
A continuació es defineix un altre instrument fonamental
per a l'anàlisi de les distribucions de probabilitat.
 |
S'anomena funció de distribució associada a una variable aleatòria
X (o també funció de distribució
de probabilitat acumulada) aquella funció F
que,
per a cada nombre real, ens dóna la probabilitat que
la variable aleatòria prengui un valor menor o igual que
aquell nombre.
És a dir
F(a) = p[X 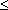 a] per cada nombre
real a. a] per cada nombre
real a. |
La funció de distribució d'una variable
aleatòria és un element de treball fonamental a
l'hora de calcular probabilitats relatives a intervals de
valors que pot prendre la variable que estudiem.
Adoneu-vos que per a una distribució
discreta amb valors enters podrem calcular així la
probabilitat d'un interval:
p(a 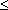 X X 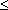 b) = F(b) –
F(a–1) b) = F(b) –
F(a–1)
Fixeu-vos, molt en
concret, en el fet que en el cas discret que ara ens ocupa,
"només" hem de restar la probabilitat acumulada fins a
a–1 si volem calcular la probabilitat de l'interval
que va des del valor a fins al valor b.
La funció de distribució F d'una
variable aleatòria discreta compleix les propietats que
s'indiquen seguidament, que caracteritzen les funcions de
distribució discretes.
- F és una funció escalonada,
monòtona creixent.
- La funció de distribució F té
límit 0 quan x tendeix a menys infinit i
límit 1 quan x tendeix a l'infinit positivament.
- F és contínua a la dreta en qualsevol
punt.
- Si x1, x2,
x3,... ,xn,... són
els valors que efectivament pren una variable aleatòria
discreta X, la seva funció de distribució
F és contínua arreu excepte en els punts
x1, x2,
x3,... ,xn,... en què
presenta discontinuïtats de salt.
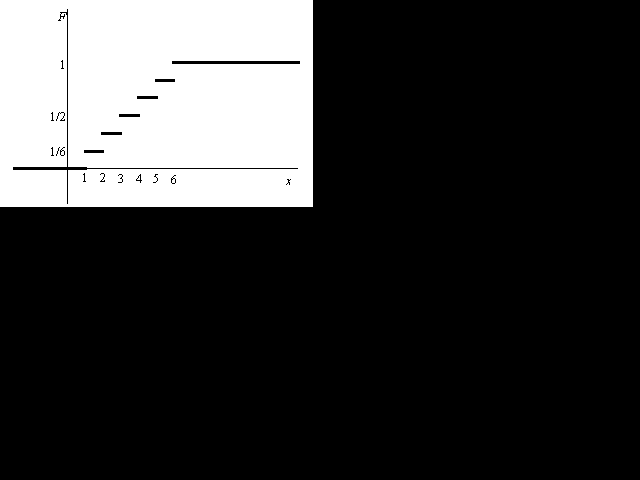
Vegeu com a exemple el gràfic de la funció de
distribució corresponent a la Distribució uniforme
discreta amb n = 6 i que pren valors {1, 2, 3,... ,6}.
De la mateixa manera que es fa en l'Estadística
Descriptiva, per les variables aleatòries també es calculen
paràmetres que acumulen informació significativa de la variable.
Seguidament definirem els paràmetres que més s'empren en
l'estudi de les variables aleatòries discretes:
 |
La mitjana de la distribució, que
es representa amb la lletra grega µ, i també rep el
nom d'esperança matemàtica, [i d'acord amb
aquesta denominació es simbolitza E(X)]
es
defineix mitjançant la fórmula 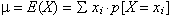 |
 |
La desviació estàndard (o
desviació tipus), definida a partir de la fórmula.
 Com en el cas dels paràmetres estadístics, el
quadrat de la desviació estàndard rep el nom de
variància.
Com en el cas dels paràmetres estadístics, el
quadrat de la desviació estàndard rep el nom de
variància.
|
|
|
|
És important indicar que les definicions
anteriors sorgeixen a partir d'un paral·lelisme amb la
fórmula de la mitjana i la desviació
estàndard d'una variable estadística discreta.
Seguidament es comenten alguns exemples.
- Si preguntem a una persona "del carrer" quantes vegades li
sembla "normal" d'haver de tirar un dau per a treure un 6
és fàcil que ens contesti "6 vegades". Aquest
valor és, en realitat, la mitjana de la
distribució de probabilitat associada a la variable
aleatòria "nombre de vegades que hem de tirar un dau fins
a obtenir un 6".
- Si tirem enlaire 20 monedes i preguntem "quantes creus podem
esperar que surtin?", la resposta intuïtiva "10" correspon
a la mitjana de la variable aleatòria "nombre de creus
que surten quan tirem 20 monedes".
- En una distribució uniforme que pot prendre els
valors {1, 2, 3,..., n} es pot demostrar que la mitjana
és (n+1)/2 i la desviació
estàndard (n–1)2/12.
|
|
|
La distribució binomial
 |
S'anomena prova de Bernouilli una
experiència simple de la qual ens interessa fixar-nos
únicament en un determinat esdeveniment A
("èxit") que té probabilitat p.
|
 |
La distribució binomial és la que
està associada a la variable aleatòria "nombre
d'èxits observats" quan es repeteix successives vegades
una experiència de Bernouilli, sempre en les mateixes
condicions i de manera independent.
|
Es representa B(n,p) la
distribució binomial que correspon a n repeticions
independents d'una experiència en la qual la probabilitat
d'èxit és p. S'acostuma a representar
q =1–p la probabilitat que no succeeixi
l'esdeveniment que estem estudiant.
Per exemple:
- "El nombre de cares que traiem
quan tirem enlaire 20 monedes, no trucades, de forma
independent" correspon una distribució binomial
B(n=20, p=1/2).
- El nombre de persones que
contestaran "SÍ" a una enquesta feta a una mostra de 500
persones que s'ha seleccionat aleatòriament en una
població en la qual el 40% opina que "SÍ"
correspon a una distribució binomial B(n=500,
p=0,4).
La fórmula que dóna la
funció de probabilitat d'una variable aleatòria
X a la qual correspon una distribució binomial
B(n,p) és
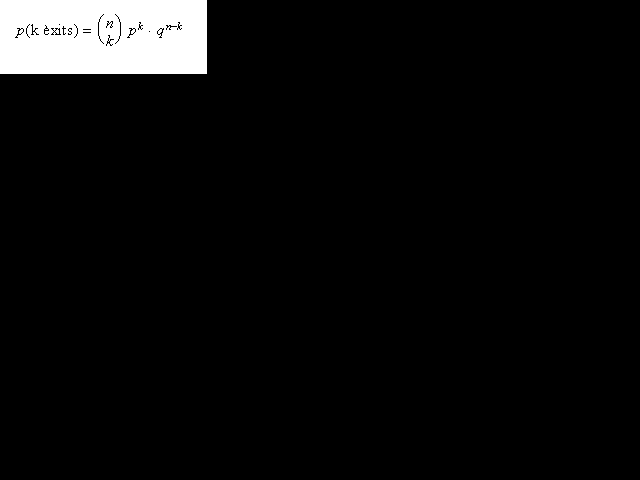 Aquesta fórmula dóna la probabilitat d'observar
k èxits d'un esdeveniment que té
probabilitat p en una prova simple quan se'n fan n
repeticions independents.
Aquesta fórmula dóna la probabilitat d'observar
k èxits d'un esdeveniment que té
probabilitat p en una prova simple quan se'n fan n
repeticions independents.
|
|
|
- Podeu consultar la deducció d'aquesta fórmula.
- L'aplicació de la fórmula anterior
és molt farragosa a «mà» és (relativament)
fàcil emprant la calculadora científica i, naturalment,
molt més àgil amb Excel... però sembla que xoquem
amb una paret insalvable si n es fa relativament gran. Tannmateix,
podrem solucionar aquest problema
amb l'estudi de la distribució normal.
La mitjana de la distribució binomial
B(n,p) té per valor µ =
n·p.
La desviació estàndard de la
distribució binomial B(n,p) és
igual a
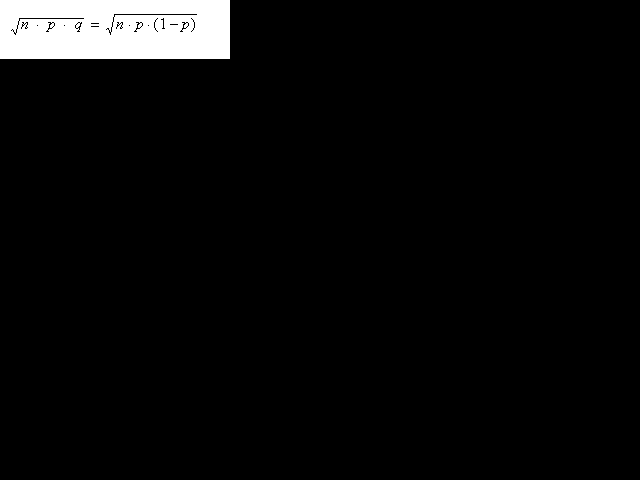 En la pràctica 1 s'exposen exemples
d'aplicació de la distribució binomial i càlculs
de probabilitats relacionats i la pràctica 2
enceta l'estudi (que reprendrem en altres mòduls) que ens diu que la distribució
binomial és el model teòric adequat per al tractament de les enquestes
d'opinió.
En la pràctica 1 s'exposen exemples
d'aplicació de la distribució binomial i càlculs
de probabilitats relacionats i la pràctica 2
enceta l'estudi (que reprendrem en altres mòduls) que ens diu que la distribució
binomial és el model teòric adequat per al tractament de les enquestes
d'opinió.
Per veure les
característiques gràfiques de les funcions de
probabilitat associades a la distribució binomial i
la influència dels paràmetres p,
probabilitat d'èxit, i n, nombre de
repeticions, podeu accedir a la pràctica 5.
|
|
|
La distribució geomètrica (de Pascal)
Estudiarem ara una altra distribució de probabilitat
associada amb la repetició d'una experiència
simple en la qual ens interessa considerar un esdeveniment
A, èxit, que es pot donar amb probabilitat
p = p(A).
 |
El model teòric associat a la variable
aleatòria que fa el recompte de vegades que cal repetir
una experiència aleatòria simple, de forma
independent, fins que s'observa l'èxit de determinat
esdeveniment, rep el nom de distribució
geomètrica de probabilitat.
|
- La variable aleatòria que considerem pot prendre els
valors 1, 2, 3, ..., n, ... (sense limitació
teòrica, hom suposa que la prova es pot anar repetint
indefinidament) i les probabilitats corresponents tenen els
valors següents:
p[X=n] = (1–p)n–1· p
expressió en la qual p representa la
probabilitat d'èxit, en cadascuna de les proves simples,
de l'esdeveniment estudiat.
- La denominació "geomètrica" de la
distribució li ve del fet que els valors de les
probabilitats d'obtenir l'èxit a la primera tirada, a la
segona, a la tercera,... (que són els valors que ens
dóna la fórmula anterior) formen una
progressió geomètrica decreixent de raó
(1-p).
- La mitjana de la distribució geomètrica
és 1/p.
- La variància de la distribució
geomètrica és
(1–p)/p2 (i la desviació
estàndard serà l'arrel quadrada d'aquest valor).
- Per exemple, si fem l'experiència de comptar quantes
vegades hem de tirar un dau enlaire de forma independent fins
que surti un 5 ens trobem en la situació de la
distribució geomètrica.
En aquest cas serà p=1/6 i per tant la mitjana
és 6. Retrobem allò que ja havíem dit: si
preguntem a una persona quantes vegades li sembla que ha de
tirar fins a treure un 5 amb un dau i ens contesta "6
vegades"... això és la mitjana o esperança
de la distribució.
- El model geomètric queda caracteritzat, doncs, ja
sigui per la probabilitat d'èxit ja sigui per la mitjana
de la distribució.
- El programa Excel no inclou la distribució
geomètrica entre les "seves" distribucions de probabilitat. És per
això que es presenta amb detall en la
pràctica 4 el procediment
per a elaborar, amb Excel, una taula de valors que permet
l'estudi de la distribució geomètrica i, en particular, ens servirà en la
pràctica 5 per a visualitzar-ne el gràfic de la funció de probabilitat.
|
|
|
La distribució de Poisson
En moltes ocasions interessa, per qüestions de tipus
pràctic, preveure el nombre de vegades que podem
esperar que es produeixi un cert esdeveniment aleatori en un
determinat període de temps. Per exemple, el nombre de
trucades telefòniques que rep una centraleta per minut
(per decidir quantes persones han de controlar la centraleta) o
bé el nombre d'avisos d'avaria que pot rebre cada dia, en
mitjana, un taller de lampisteria...
Per fer aquesta previsió caldrà un treball
estadístic previ i l'ajust amb un model escaient.
L'estudi d'aquest tipus de distribucions que fan el recompte del
nombre de vegades que un esdeveniment aleatori s'ha produït
en un interval de temps correspon, si es compleixen certes
condicions, a un mateix model teòric que s'anomena
Distribució de probabilitat de Poisson.
En el marc de la sèrie
"Estadística i Atzar" (Open University, B.B.C.,
versió de TV3 per a Universitat Oberta) hi ha dues
unitats que poden ajudar a entendre aquest model: Un model
de probabilitat pels esdeveniments rars" i "El model de
Poisson". Si hi teniu ocasió... no dubteu a mirar
aquests dos vídeos!
- Perquè el model de Poisson sigui escaient ha de
passar...
- que no hi hagi simultàniament dos "èxits" de
l'esdeveniment.
- que un "èxit" de l'esdeveniment sigui independent
dels "èxits" anteriors.
- Per exemple, sí que corresponen al model...
- el nombre de trucades telefòniques que rep per minut
la centraleta del Departament d'Ensenyament.
- el nombre de partícules radioactives comptabilitzades
cada 5 segons per un comptador Geiger situat a prop d'un focus
radioactiu.
- el nombre de cotxes que circulen per minut en un tram de
carretera de circulació lliure i no massa intensa.
- En canvi no correspondran al model que volem estudiar:
- el recompte del nombre de persones que entren per minut en
uns grans magatzems, perquè de vegades hi entren grups de
persones simultàniament.
- el nombre de cotxes que circulen cada mig minut en les
rodalies d'un semàfor. La regulació del
semàfor fa que la circulació d'un cotxe no sigui
independent de la d'un altre.
 |
La distribució de probabilitat de Poisson
s'associa a la variable aleatòria que pren com a valors
el nombre de vegades que s'ha produït en un període
de temps fixat un esdeveniment aleatori del qual els
"èxits" s'observen de manera no simultània i
independent.
|
- El paràmetre que caracteritza la distribució
de Poisson és la mitjana del nombre vegades que
l'esdeveniment observat es produeix en el període de
temps fixat: aquesta és la mitjana de la
distribució.
- Els valors xi que pren la variable
aleatòria X valen, doncs, {0, 1, 2, ... ,k ,
...}, sèrie que no té un terme final tot i que la
probabilitat dels valors alts és pràcticament
zero. La funció de probabilitat corresponent al model de
Poisson ve donada per l'expressió
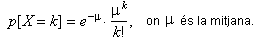
- Per una variable aleatòria amb distribució de
Poisson es compleix que la mitjana i la variància
coincideixen:
E(X) =
µ; 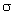 2 = µ 2 = µ
i, precisament perquè coincideix amb la mitjana de la
distribució, el paràmetre constant que apareix en
la fórmula de la distribució de Poisson i la
caracteritza es representa habitualment com a µ (tot i
que l'Excel l'anomena Lambda).
En la pràctica 5 podeu
estudiar les característiques gràfiques de les
funcions de probabilitat associades a distribucions de Poisson
i la influència del paràmetre µ.
Quan pensarem que una distribució empírica de
dades pot tenir com a model plausible la distribució de
Poisson?
Quan reprodueixi les principals característiques d'aquest
model teòric, a saber:
- Perfil de l'histograma en forma de L, en especial amb
una llarga "cua" cap a la dreta, que serà
més pronunciada com més petit sigui el valor de
µ
- Mitjana i variància amb valors molt semblants.
- Mode molt a prop del valor de la mitjana.
Si tot això succeeix... el model de Poisson és
l'adequat per modelitzar l'experiència que estudiem. Una
vegada valorada com a consistent aquesta possibilitat, per
trobar µ s'han d'aplicar tècniques
estadístiques i d'estimació: calcularem la
mitjana de la distribució estadística estudiada i
pensarem que aquest valor ha de ser el paràmetre µ
que caracteritza el model. de Poisson.
El contrast de les dades amb el model comença amb aquesta visió
intuïtiva i després, per comprovar la bondat de l'ajust, calen
tècniques estadístiques que s'exposen al mòdul
6.
Hem presentat una situació que sovint porta cap al model
de Poisson. Tanmateix hi ha una altra forma de trobar-lo que
és important de comentar.
 |
La distribució de Poisson és, també, el model que resulta com a límit
d'una distribució binomial en la qual es fan moltes
repeticions [n (molt) gran] però l'èxit
és un «esdeveniment rar» [p (molt)
petit].
|
- En aquests casos la mitjana n·p caracteritza la
distribució perquè els valors de la
distribució binomial B(n , p) si
n és gran i p petit (p < 0,1)
són molt aproximadament iguals que els valors de la
distribució de Poisson de mitjana µ =
n·p.
La pràctica 6 us permetrà
constatar empíricament aquest fet que la distribució de Poisson
sorgeix com a límit de la distribució binomial. Observeu que
l'avantatge de poder aplicar aquesta aproximació de la distribució
binomial B(n,p) que resulta de considerar per a ella
els valors de la distribució de Poisson, és que, si realment
és escaient de fer-ho...
- No caldrà saber els valors de n i de p
(tasca a vegades impossible) sinó la mitjana de la
distribució, amb la qual ja podrem calcular les
probabilitats associades a l'experiència.
- Encara que es poguessin saber els valors de n i de
p, com que ja s'ha dit que aquesta situació
correspon a valors de n molt grans, seria impracticable
la fórmula de la distribució binomial; en canvi la
fórmula de la distribució de Poisson sí que
ens permetrà calcular els valors de les
probabilitats.
Vegeu, per acabar, uns exemples d'aquesta situació:
- El primer de tots correspon a dades reals,
històriques i, sense cap dubte, ens permetrà
entendre la denominació de model de probabilitat per
als esdeveniments rars que es cita sovint
per a la distribució de Poisson.
La taula següent dóna l'estadísitica del
nombre de morts per una coça de cavall a
l'exèrcit prussià, en dades observades en un gran
nombre de cossos d'exèrcit durant un llarg
període.
Nombre de defuncions
per cos
d'exèrcit i any |
0 |
1 |
2 |
3 |
4 o més |
| Freqüència absoluta |
109 |
65 |
22 |
3 |
1 |
|
Total de dades observades |
200 |
En cada cos d'exèrcit hi ha un nombre molt elevat de
soldats, però desconegut per a nosaltres i no coincident
en tots els casos. La probabilitat que un soldat determinat en
un d'aquests cossos d'exèrcit mori d'una guitza de cavall
és molt i molt petita. Si el repartiment d'aquestes
defuncions és degut a l'atzar el model adequat
serà la distribució de Poisson, com es pot
desprendre de l'anàlisi intuïtiva de les
característiques d'aquest recull de dades
empíriques. Us proposarem un
exercici sobre aquestes dades, per al contrast de les dades amb el model, en el mòdul 6
- El nombre d'errades en una pàgina
impresa és un altre exemple clàssic de la
distribució de Poisson (ara potser poc actual
perquè cada vegada hi ha mitjans més sofisticats
de correcció).
En cada pàgina hi ha un gran nombre de caràcters tipogràfics;
sempre molt gran però no coincident d'una pàgina a una
altra. La probabilitat que hi hagi error en un d'aquests caràcters
és molt petita. Tanmateix, es pot fer un compte de la mitjana
d'errades per pàgina i es pot suposar que la distribució
de les errades és fruit de l'atzar. Per això el model
de Poisson és adequat. Podeu estudiar numèricament aquest
exemple en la pràctica 4.
- El nombre de perles naturals de qualitat que recullen
els buscadors d'ostres d'una factoria al llarg d'un dia es cita també com a exemple en què
escau Poisson.
Entre tots els pescadors al llarg d'un dia es capbussen moltes vegades
i treuen, doncs, un nombre molt gran d'ostres. La probabilitat que una
ostra tingui perla de qualitat és molt i molt petita. La mitjana
d'ostres de qualitat per dia vé donada per una distribució
de Poisson. Ens referirem a aquest exemple en un dels exercici
8.
Per acabar ens fixarem en la semblança del plantejament
inicial (compte d'un cert esdeveniment aleatori en un
període de temps) i aquest que donem ara
(límit de la distribució binomial per n molt
gran i p molt petit).
- Hem donat com a exemple el nombre de
trucades telefòniques que rep per minut la centraleta del
Departament d'Ensenyament. Seria bo que, per regular el
servei telefònic, al Departament tinguessin
comptabilitzada la mitjana d'aquest nombre que permetria
establir la fórmula de la distribució de Poisson
que modelitza el problema.
Ara bé, un minut es pot imaginar dividit en un gran
nombre n de períodes de temps molt petits, per
exemple, mil·lèsimes de segon. Hem de pensar que la
probabilitat p de rebre una trucada telefònica en
un període concret d'una mil·lèsima de segon
és molt petit. Però llavors, amb n molt
gran (però no conegut) i p molt petit, la mitjana
n·p té un valor apreciable, que és el
que es pot conèixer
estadísticament..
Per això és vàlid el model de Poisson en
aquesta i altres situacions semblants.
De vegades es diu que la distribució de Poisson
P(µ) resulta com a límit de la
distribució binomial B(n, p) quan
n es fa molt gran («tendeix a infinit»),
p és molt petit i es pot assumir que es manté constant
n·p = µ.
|
| |
|
 |
| |
|
| |
Aclariments, ampliacions, comentaris |
| |
|
 |
Sobre la mitjana i la desviació estàndard d'una variable aleatòria
Hem dit que les
definicions de mitjana i desviació estàndard d'una
distribució de probabilitat sorgeixen a partir d'un
paral·lelisme amb la fórmula de la mitjana i la
desviació estàndard d'una variable
estadística discreta.
En una distribució estadística, si
xi són els valors observats,
F[X=xi] les corresponents
freqüències absolutes i N el nombre
d'observacions, la fórmula de la mitjana es pot
escriure
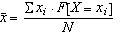
Però si ens adonem que podem treure factor comú i
que F[X=xi]/N són les
freqüències relatives dels valors observats,
f[X=xi], podem re-escriure la
definició de la mitjana d'una distribució de dades
estadístiques de la manera següent:
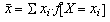
Ara bé, si us fixeu en la visió intuïtiva de les
probabilitats p[X=xi] com a valor al
qual tendeixen les freqüències relatives
f[X=xi] si es fan moltes repeticions de
l'experiència, podreu interpretar la mitjana d'una
distribució de probabilitat com el valor al qual tendiria
a acostar-se la mitjana dels valors observats en una llarga
repetició de l'experiència a la qual correspon la
variable aleatòria que estudiem. Anàlogament la
desviació estàndard dels valors observats en
moltes repeticions de l'experiment tendeix a acostar-se a la
desviació estàndard de la distribució de
probabilitat.
- Pel que s'acaba de comentar la mitjana d'una
distribució de probabilitat és un estimador del
valor esperat en l'experiència corresponent i, de
fet, de vegades la mitjana rep el nom de valor esperat .
No s'ha de confondre, però, de cap manera "valor esperat"
–que ja s'ha dit que cal interpretar com "valor
mitjà, a la llarga"– amb "valor més
probable".
- La mitjana d'una variable aleatòria s'anomena
també esperança matemàtica,
denominació que prové de la consideració
de jocs d'atzar, de gran importància per al
desenvolupament històric de la teoria de probabilitats,
en els quals la mitjana s'interpreta com la mitjana dels
"guanys" que hom pot esperar obtenir si juga repetidament a
l'esmentat joc (sempre pèrdues, a la llarga!).
|
| |
|
 |
| |
|
 |
Deducció de la fórmula de la
distribució binomial
La fórmula és la següent:
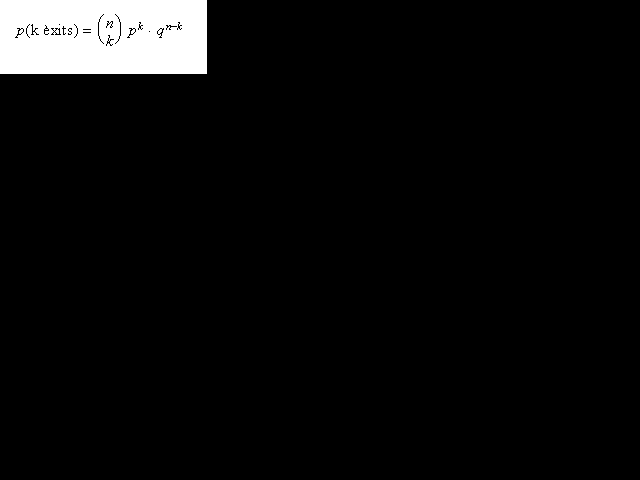
Aquesta fórmula dóna la probabilitat que en
n repeticions independents d'una experiència
s'esdevinguin k èxits. El valor d'aquesta
probabilitat prové de les consideracions que exposem
seguidament, la rigorització de les quals escapa a aquest
curs.
- Si examinem el cas que en les k primeres
realitzacions de l'experiència resulti l'èxit i en
les n-k següents no, la fórmula del producte
de les probabilitats ens porta de seguida a què aquest
fet té probabilitat p·p·...(k
vegades)...·p·q·q·...(n-k vegades)...·q =
pk·qn-k.
- Ara bé, hi ha moltes altres maneres de trobar
k èxits i n-k no èxits. El nombre
combinatori que apareix a la fórmula (dit "n sobre
k") indica quantes són aquestes maneres, totes les
quals tindrien la mateixa probabilitat. Totes aquestes
probabilitats s'han de sumar per tenir la probabilitat total de
k èxits.
- Finalment, si hem de sumar una colla de sumands iguals tots
ells a pk·qn-k i el nombre de
sumands ve donat pel nombre combinatori n sobre k,
en resulta el valor indicat a la fórmula.
|
| |
|
 |
| |
|
 |
Els càlculs dels valors de la
distribució binomial, ens fan xocar amb una paret
insalvable quan n és gran?
- Per valors de n molt petits és recomanable
deduir els valors de les probabilitats d'un experiment que
segueixi el model binomial mitjançant l'estudi dels
diagrames d'arbre.
- Si n augmenta una mica heu de saber que els valors
dels nombres combinatoris es poden obtenir amb el
desenvolupament del triangle de Tartaglia.
- També es pot emprar una calculadora científica
i la fórmula dels nombres combinatoris, que inclou
factorials, per a obtenir els valors de les probabilitats de la
distribució binomial.
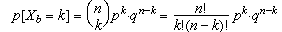 Però els factorials arriben a tenir valors tan grans que
aviat ultrapassen la capacitat de les calculadores manuals (en
els models més habituals el càlcul de n!
per a valors de n > 70 dóna E per
aquesta raó).
Però els factorials arriben a tenir valors tan grans que
aviat ultrapassen la capacitat de les calculadores manuals (en
els models més habituals el càlcul de n!
per a valors de n > 70 dóna E per
aquesta raó).
- Segurament pensareu que amb l'Excel es resoldrà
aquesta dificultat. En part sí, però els
càlculs "també superen l'ordinador" i si n es fa molt gran trobareu anomalies de funcionament (valors que donen 0 sense ser-ho en realitat o errors).
- Hem xocat, doncs, amb una paret? No!!! L'aproximació
de la distribució binomial mitjançant la normal en
general (o el model de Poisson en casos extrems per a n
molt gran i p molt petit) ens permeten salvar aquesta
dificultat.
|
| |
|
 |

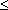 X
X 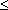 b) = F(b) –
F(a–1)
b) = F(b) –
F(a–1)