| |
|
| |
|
|
|
Els contrastos d'hipòtesis. La prova
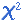
 |
| |
En aquest document es fa una presentació conceptual dels contrastos
d'hipòtesi, amb el vocabulari que els és associat, juntament
amb una exposició ben detallada de la prova de khi quadrat de la
bondat de l'ajust i la seva aplicació a diverses situacions
pràctiques. L'exemple introductori que es presenta seguidament
i d'altres d'igualment il·lustratius per a la prova de khi quadrat
es comencen a treballar a la pràctica 1.
També s'estudia l'aplicació de la prova de khi quadrat
a l'anàlisi de taules de doble entrada, tant des d'un punt de vista
teòric com a la pràctica 3.
|
| |
|
 |
Freqüències observades versus
freqüències esperades |
| |
|
| |
En aquest apartat es
presenta un exemple introductori, inspirat parcialment en el vídeo
La bondat de l'ajust de la sèrie Estadística i
Atzar (Open University, BBC, versió de TV3 per a Universitat Oberta).
Resultat experimental: valors observats
Una investigadora fa encreuaments entre flors blanques
(caràcter B al fenotip, provinent de dos gens B, genotip BB) i
flors vermelles (caràcter V al fenotip, genotip VV). Cada flor
de la primera generació de descendents té genotip BV (un
gen de cada progenitor, primera llei de Mendel). Si suposem que cap
d'aquests caràcters és dominant sobre l'altre, totes les
flors seran roses.
Seguidament, continua l'experiment: encreua aquestes flors
roses, és a dir, fa encreuaments d'una flor amb genotip BV i una
altra flor amb genotip BV. Poden aparèixer flors amb genotip BB
(resultat: flor blanca), BV o VB (flor rosa), VV (flor vermella). Ens
diu que ha obtingut 444 flors, de les quals 102 són blanques, 246
roses i 96 vermelles. Aquests seran els valors observats en la seva experiència.
Model teòric: valors esperats
Segons les lleis de Mendel, per a la segona generació
de descendents es combina un gen de cada progenitor i totes les possibilitats
de combinar un gen d'un progenitor amb un de l'altre tenen la mateixa
probabilitat. Aquestes possibilitats són: BB (resultat: flor blanca),
BV o VB (flor rosa), VV (flor vermella). Segons aquesta llei, s'espera
que la quarta part de les flors siguin blanques, la meitat roses i la
resta, és a dir, una altra quarta part, vermelles; tanmateix, el
creuament de flors és un experiment aleatori, en què intervé
l'atzar, i per això hem de concretar l'enunciat anterior i substituir-lo
per aquest altre:
Hem d'esperar que les freqüències de flors
blanques, roses i vermelles estaran aproximadament en la proporció
1:2:1. D'un total de 444 flors, els valors esperats són
111, 222, 111, però l'atzar fa que els valors reals estiguin al
voltant d'aquestes quantitats.
La valoració de la bondat de l'ajust
La pregunta que ens plantejarem (i mirarem de respondre)
al llarg d'aquest mòdul es pot formular així: Estan d'acord
les dades obtingudes empíricament amb la teoria genètica?
Ja sabem que en el resultat de l'encreuament hi ha una influència
de l'atzar (o de la probabilitat, com vulgueu). Tenim un model teòric
(l'esmentada llei de Mendel) i ens preguntem si la influència de
l'atzar pot haver donat com a resultat, de manera versemblant, el nombre
de flors de cada color observades. La valoració numèrica
d'aquesta possibilitat és el que rep el nom de contrast d'hipòtesis
o prova estadística (o també test estadístic,
tot i que no és aquest el mot acceptat pels lingüistes); en
aquest cas, es tracta de la comprovació de la bondat de l'ajust.
|
| |
|
|
|
 |
El llenguatge associat als contrastos d'hipòtesis |
|
|
| |
L'objectiu d'aquest mòdul
és entendre què significa un contrast o una prova d'una hipòtesi
estadística.
De les accepcions que ens dóna el diccionari per al mot hipòtesi,
la que més d'acord està amb el sentit que se li dóna
en aquest capítol és aquesta:
Teoria provisionalment adoptada per explicar certs fets.
 |
En els contrastos d'hipòtesis rep
el nom d'hipòtesi nul·la, HN, H0,
l'afirmació de la qual es vol confrontar la veracitat; en
aquest cas, que el model estadístic que hem triat per al
nostre estudi (i que es caracteritza mitjançant uns valors
esperats) és l'adequat. |
En l'exemple introductori, la hipòtesi nul·la és
la suposició que la primera llei de Mendel és vàlida.
La finalitat del test consisteix a decidir, a la vista de les dades
obtingudes i els càlculs necessaris, quina de les dues situacions
següents es dóna:
- Es pot entendre que les diferències entre els valors observats
i els valors esperats són fruit de l'atzar i no ens han de fer
dubtar del model, i en aquest cas podem seguir admetent com a vàlida
la hipòtesi nul·la.
- La discrepància entre els valors obtinguts empíricament
i el model teòric és significativament gran i podem rebutjar
el model teòric.
Per entendre l'actitud d'un investigador
en una prova estadística encaminada a confrontar unes dades empíriques
amb un model teòric i valorar la bondat de l'ajust, és
molt interessant el paral·lelisme següent amb un tribunal de
justícia:
| |
Tribunal de justícia |
Prova estadística |
| Demana evidència de |
Culpabilitat |
Inadequació de les dades
al model teòric |
| Hipòtesi nul·la |
Innocent, no culpable |
Model teòric correcte |
| Hipòtesi alternativa |
Culpable |
Model teòric no vàlid |
| Actitud |
S'accepta no culpable fins que
es demostra el contrari
de manera clara i precisa |
S'accepta que el model teòric
establert
és vàlid excepte en el cas que
les dades empíriques donin un
testimoni evident en contra |
Parem atenció a l'exemple: 102, 246 i 96 flors, respectivament,
representen moltes més flors roses (i menys de les altres) respecte
a les esperades 111, 222 i 111 del total de 444 flors. Aquestes dades
ens permetrien dubtar seriosament de la llei de Mendel o bé la
diferència pot ser fruit de l'atzar? La prova de la bondat de l'ajust
es planteja mesurar fins a quin punt els valors obtinguts difereixen dels
valors esperats, perquè, evidentment, si els veiem molt semblants,
no ens cal cap demostració per seguir acceptant el model. Tanmateix,
la influència de l'atzar en els resultats de les experiències
que estudiem fa que mai puguem estar segurs de les nostres afirmacions.
Mai podem estar del tot segurs que una llei empírica, com és
ara la llei de Mendel, falla (ni que totes les flors sortissin roses).
Tenim sempre un risc d'equivocació si pretenem rebutjar estadísticament
una hipòtesi. Per això, abans d'elevar a definitiva la nostra
conclusió (i fins i tot abans de començar l'experiment),
hem de quantificar aquest risc, és a dir, la probabilitat d'equivocar-nos.
Abans de donar una nova definició, completarem amb un detall (en
què esperem que estareu d'acord) el símil del tribunal de
justícia.
|
Si hom rebutja la
innocència d'un acusat (rebuig de la hipòtesi
nul·la) i aquesta decisió és errònia,
aquest error és conceptualment molt més seriós
que no pas el que es dóna en la situació de mantenir
la consideració d'innocent (no rebutjar la hipòtesi
nul·la, seguir-la considerant vàlida) per a una
persona que realment és culpable.
|
 |
En un experiment aleatori encaminat a la comprovació
d'una hipòtesi estadística, s'anomena risc de primera
espècie la probabilitat de rebuig de la hipòtesi
nul·la en cas que sigui correcta. |
Si som agosarats i acceptem un alt risc, podem deduir fàcilment
que hem descobert que la llei de Mendel falla. En canvi, si som massa
prudents i volem seguretat, és a dir, que el risc d'equivocar-nos
sigui quasi nul, ens podran enganyar molt sovint amb proves estadístiques,
perquè mai trobarem proves estadístiques segures. Aquí
hi trobem el joc de la teoria de probabilitats. La fixació del
risc que estem disposats a admetre per formular el rebuig de la hipòtesi
nul·la (model teòric pressuposat correcte) és un procediment
no objectiu, sinó que va lligat a diversos aspectes subjectius.
 |
El màxim risc de primera espècie
que es vol admetre en la realització d'una prova estadística
de contrast d'unes dades amb un model rep el nom de nivell de
significació de la prova i és representat habitualment
per la lletra grega alfa. |
- L'experiència dels que treballen en estadística demostra
que la fixació d'un nivell de significació del 5 %
és prou correcta i equilibra les dues opcions que hem comentat
(l'agosarada i la conservadora).
Quan ja hem acordat el nivell de significació amb què
volem treballar i emprenem la realització d'un test, podem establir
en quines circumstàncies arribarem a rebutjar la hipòtesi
nul·la.
 |
S'anomena regió crítica
el subconjunt dels valors que, en cas de ser observats, ens fan
rebutjar la hipòtesi nul·la. |
La regió crítica s'estableix moltes vegades no tant segons
les freqüències observades, sinó segons algun estadístic
que es calcula a partir d'aquestes, en el benentès que un estadístic
és una característica numèrica calculada a partir
de les dades obtingudes en una realització de l'experiència
i pot variar d'una realització a una altra. Si tenim ben conegut
el model teòric de variabilitat d'un estadístic, això
ens ajudarà en les nostres conclusions. Tot seguit, expliquem quin
és l'estadístic que ens pot ajudar en el problema que tenim
plantejat: la mesura de la bondat de l'ajust entre unes freqüències
observades i unes freqüències esperades.
|
|
|
 |
La prova de khi quadrat de la bondat de l'ajust |
| |
|
| |
El camí intuïtiu per fer un càlcul que permeti valorar
el grau d'ajust (o de desajust) entre les freqüencies observades
(empíriques) i les freqüències esperades (teòriques)
és el següent:
- La idea de què partim per mesurar la discrepància entre
unes i altres freqüències és, naturalment, calcular
les diferències entre unes i altres.
- Ara bé, aquestes diferències s'han de positivar, perquè
tant s'aparta del model una diferència en un sentit com en un
altre. Les elevarem al quadrat com es fa amb la desviació estàndard,
per exemple. Si no ho fem així, unes desviacions es compensaran
amb unes altres en lloc de sumar-se.
- Seguidament, cal relativitzar o ponderar les diferències quadràtiques
obtingudes, perquè és evident que no és igualment
significatiu treure 22 flors roses més del compte en un encreuament
que ha donat 444 flors, que treure 22 flors roses més del compte
si haguéssim trobat 4.444 flors com a resultat de l'encreuament.
Aquesta relativització es fa prenent com a referència
els valors esperats.
- Finalment, és clar, cal sumar per obtenir la discrepància
total.
Les idees anteriors marquen clarament el camí per definir l'estadístic
que ens interessa.
- Si Oi representa la freqüència observada
en cada classe, Ei la freqüència esperada
en aquella classe d'acord amb el model teòric que volem confrontar,
es defineix un estadístic que es representa com a X2
mitjançant un sumatori que s'estén a totes les classes
de valors observats.
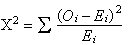
- Convé que observeu que no tots els valors de les diferències
Oi–Ei són
independents l'un de l'altre, sinó que la seva suma és
0. Si hi ha n classes de valors, només n–1
de les diferències esmentades són independents. Per exemple,
si hem observat 22 flors roses de més respecte a les esperades,
és segur que hem obtingut menys flors blanques i menys flors
vermelles de les esperades, 22 en total.
Suposant que la hipòtesi nul·la és correcta,
és a dir, que el model donat per les freqüències esperades
s'adiu a l'experiència que estudiem, llavors l'estadístic
X2 té un model teòric perfectament conegut:
si hi ha n classes de valors és la distribució khi
quadrat amb n – 1 graus de llibertat, representada com a 
Observacions:
- Convé que conegueu com s'escriu la lletra grega khi (també
designada com a qui o ji):
 i sapigueu que la majúscula es reserva per a l'estadístic
i la minúscula per representar la distribució de probabilitat.
i sapigueu que la majúscula es reserva per a l'estadístic
i la minúscula per representar la distribució de probabilitat.
- La distribució khi quadrat amb k graus de llibertat
es presenta a la pràctica 6
del mòdul 5 com a suma de quadrats de k distribucions
normals estàndards. Com que es pot demostrar que, per cada classe,
(O-E)2/E es distribueix com una normal estàndard
i com que només hi ha n - 1 d'aquestes observacions independents,
el model per a l'estadístic X2 és la distribució
khi quadrat amb n – 1 graus de llibertat.
A l'exemple que serveix de fil conductor a aquesta explicació,
el càlcul de l'estadístic X2 dóna:
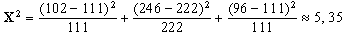
Adoneu-vos que l'estadístic X2 té un valor més
petit com més bo és l'ajust de les dades amb el model.
Hem obtingut un valor de l'estadístic X2 que mesura
la discrepància entre les freqüències observades i
les freqüències esperades. Però, el número 5,35
que ens ha resultat representa molt o bé és poc, com a discrepància
total? Si 5,35 representés un valor suficientment alt, rebutjaríem
la validesa de la hipòtesi nul·la (o faríem nous experiments).
Per decidir si és suficientment alt, hem de consultar el model
teòric d'aquest estadístic (la distribució khi quadrat
amb dos graus de llibertat en aquest cas) i fixar-nos en el nivell de
significació que haguem decidit d'acceptar.
Hi ha dos enfocaments diferents per fer la confrontació de l'estadístic
X2 obtingut amb la distribució khi quadrat, que dóna
el model teòric de l'estadístic. Seguidament comentarem
aquestes dues visions que permeten treure conclusions de la prova de khi
quadrat de comprovació de la bondat de l'ajust (Chi-square
Goodness-of-fit Test, degut a K. Pearson, 1900).
La pràctica 1 mostra com es pot obtenir
amb l'Excel el valor de l'estadístic X2, il·lustra
els dos punts de vista que es comenten seguidament i comenta quin és
el més apropiat.
- Primer punt de vista: correspon a l'establiment d'una regió
crítica que indica quins són els valors de l'estadístic
X2 que ens fan rebutjar la hipòtesi nul·la. Aquest
pot ser el procediment emprat en el treball manual, que podem fer mitjançant
la consulta de taules publicades als manuals d'estadística, com
és ara la que transcrivim seguidament:
Graus de
llibertat |
Probabilitat
acumulada en la distribució khi quadrat |
| 0,90 |
0,95 |
0,975 |
| Nivell de significació
(alfa) |
| 10 % |
5 % |
2,5 % |
| 1 |
2,71 |
3,84 |
5,02 |
| 2 |
4,61 |
5,99 |
7,38 |
| 3 |
6,25 |
7,81 |
9,35 |
| 4 |
7,78 |
9,49 |
11,14 |
| 5 |
9,24 |
11,07 |
12,83 |
| 6 |
10,64 |
12,59 |
14,45 |
| 7 |
12,02 |
14,07 |
16,01 |
| 8 |
13,36 |
15,51 |
17,53 |
| 9 |
14,68 |
16,92 |
19,02 |
| 10 |
15,99 |
18,31 |
20,48 |
| 11 |
17,28 |
19,68 |
21,92 |
| 12 |
18,55 |
21,03 |
23,34 |
| 13 |
19,81 |
22,36 |
24,74 |
| 14 |
21,06 |
23,68 |
26,12 |
| 15 |
22,31 |
25,00 |
27,49 |
Fixem-nos en l'exemple:
- Hem calculat X2 =
5,35; recordem que en aquest cas escau la distribució khi
quadrat amb dos graus de llibertat i imaginem que volem treballar
amb un nivell de significació del 5 %. Mirem a la taula anterior,
a la fila de 2 graus de llibertat, i la columna del 5 % per al nivell
de significació (o, equivalentment, 0,95 com a probabilitat
acumulada). Hi veiem 5,99.
- Què ens diu aquest valor? Que,
sota la hipòtesi que la llei de Mendel sigui vàlida,
si fem el càlcul de l'estadístic X2
corresponent a l'experiment ressenyat
p[X2 < 5,99] = 0,95.
- Equivalentment, això permet
dir que p[X2 > 5,99] = 0,05 = 5 %, i
podem afirmar que aquest conjunt de valors de l'estadístic
X2 constitueix la regió crítica
de la prova (amb un nivell de significació del
5 %). Efectivament, si aparegués un nombre d'aquest conjunt
com a valor de l'estadístic X2, podríem
rebutjar la hipòtesi nul·la (amb un nivell de
significació del 5 %) perquè, com que la probabilitat
de trobar-nos amb algun d'aquests valors és només
del 5 %, aquest serà el risc d'error màxim que tindrem
si traiem la conclusió que la hipòtesi nul·la
no és correcta.
- Això és així perquè
la probabilitat que hem esmentat està calculada pensant que
la hipòtesi nul·la és certa. Si amb aquesta hipòtesi
la probabilitat de trobar un nombre de la regió crítica
és menor del
5 %, aquesta mateixa és la probabilitat d'error (risc)
en cas que neguem la hipòtesi (i recordem que s'ha definit,
precisament, que nivell de significació del 5 % vol dir que
aquest és el risc màxim que acceptem).
- Però aquest no és el
cas en què estem; hem trobat 5,35 com a valor de X2,
i aquest no és un valor de la regió crítica.
Conclusió: els resultats observats en el nostre encreuament
de flors roses no permeten pas de cap manera dubtar de la llei de
Mendel. Encara que ens pogués semblar que els resultats s'apartaven
força d'allò que es podia esperar, no tenim criteris
suficients per rebutjar la hipòtesi nul·la (la validesa
de la primera llei de Mendel). Hem d'entendre que les discrepàncies
observades són fruit de l'atzar; no són significatives
en un nivell de significació del 5 %.
- Segon punt de vista: correspon a la consideració de
l'anomenat valor p del valor de X2 observat,
que seguidament definim.
- En l'aplicació d'una prova estadística, s'anomena valor
p d'un nombre real (o valor de probabilitat, en anglès
p value, en castellà valor p), la probabilitat
que l'estadístic estudiat tingui un valor més gran que
a. En el cas que ara ens ocupa, p[X2>a],
en el benentès que la probabilitat està calculada sota
la hipòtesi nul·la, suposant que és vàlid
el model teòric donat per les freqüències esperades.
- Adoneu-vos que, si estem contrastant unes freqüències
observades amb unes freqüències esperades i resulta que
el valor calculat per a l'estadístic X2 és
X2 = a, el valor p associat a aquest nombre
a representa el risc d'error que tenim si, comptant amb aquesta
observació, rebutgem la hipòtesi nul·la.
- El punt de vista que ara comentem és el més emprat en
el treball amb l'ordinador. Cal que comparem el valor p corresponent
a les nostres dades (aquesta és la informació que ens
dóna l'ordinador) amb el risc màxim que volem acceptar
(que està prefixat i que, recordeu-ho, s'anomena nivell de
significació de la prova) per decidir si hem de mantenir
com a vàlida la hipòtesi nul·la o bé tenim
criteris per rebutjar-la. Ja hem dit que la pràctica 1 és la que ens ensenya a treure
conclusions pràctiques del test de khi quadrat.
- A l'exemple que hem analitzat, l'Excel ens mostra que el valor
p de 5,35 en una distribució khi quadrat amb 2 graus de llibertat
és 0,0689.
- Això vol dir que es compleix p[X2 >
5,35] = 0,0689 = 6,89 %. Així, doncs, si comptem amb el valor
5,35 que hem observat per a l'estadístic X2
i insistim a rebutjar la hipòtesi nul·la (llei de Mendel
vàlida), tenim un risc d'equivocació del 6,89 % que
ningú amb bon seny acceptaria per dubtar de la validesa de
la llei de Mendel.
- El valor p ens el dóna el programa Excel. La resta
són deduccions nostres.
|
| |
|
 |
Anàlisi de taules creuades mitjançant
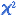 |
| |
|
| |
Al mòdul
3 es va comentar a bastament que per al tractament conjunt de dues variables
convé començar per tenir els valors de les freqüències
observades disposats en una taula de doble entrada (taula creuada o taula
de contingència).
Per estudiar el comportament de les dues variables (la
relació que podem constatar-hi), es van presentar tècniques
intuïtives: anàlisi dels percentatges de la taula (globals,
per files o per columnes, segons el tipus d'estudi que vulguem fer). Veurem
tot seguit que la prova de khi quadrat serveix com a criteri numèric
per explicar si les diferències que podem observar d'un cop d'ull
són estadísticament significatives o podrien ser fruit de
l'atzar.
S'ha de comentar el fet que aquest estudi entra en el camp de l'estadística
inferencial. La qüestió que resoldrem serà la següent:
suposant que hem pres una mostra d'una població i, pel que fa a
les dues variables estudiades, hem obtingut aquests valors, què
podem pensar de les variables considerades en el conjunt de la població?
Veurem dues maneres d'enfocar el problema: la recerca de l'homogeneïtat
d'una de les variables (variable de resposta) respecte a l'altra variable
(variable de classificació) o bé l'estudi de la independència
entre variables si aquestes juguen un mateix paper. És per
això que analitzarem amb detall dues proves basades en el test
de khi quadrat, una sota cada punt de vista. El que varia en un cas i
en l'altre, segons l'enfocament que li volem donar, és la forma
d'arribar a les freqüències esperades (enfocaments teòrics
diferents), però veurem també que a la pràctica donen
el mateix resultat.
|
| |
|
 |
Prova d'homogeneïtat |
| |
|
| |
El concepte d'homogeneïtat
s'exposa de manera intuïtiva tot dient que no hi ha diferència
en la resposta (segona variable) pel que fa als diversos grups en què
es classifica la primera variable. Quin aspecte esperem que ha de tenir
una taula creuada que reflecteix els valors emparellats de dues variables
si pressuposem que hi ha homogeneïtat en la resposta?
Recordarem tot seguit un exemple
il·lustratiu que ja ens ha servit a la part de fonaments del
mòdul 3; ara ens fixarem en l'aspecte numèric i no en el
conceptual. Hi ha sospites que en uns exàmens, la resposta (apte/a,
no apte/a) no és homogènia en els grups donats per la variable
de classificació (home, dona).
Es presenta la taula que podeu veure a l'esquerra de
la qual es conclou, intuïtivament, que no hi ha homogeneïtat
en la resposta perquè si s'elabora la taula de percentatges per
files, que teniu seguidament a la dreta, s'observen diferències
ben grans d'una fila a una altra:
| |
Aptes |
No aptes |
Total |
| Homes |
40 |
40 |
80 |
| Dones |
20 |
40 |
60 |
| Total |
60 |
80 |
140 |
|
|
| |
Aptes |
No aptes |
Total |
| Homes |
50% |
50% |
100% |
| Dones |
33,3% |
66,6% |
100% |
| Total |
42,9% |
57,1% |
100% |
|
Ara bé, l'exemple continuava, i
per raonar que sí que hi havia uniformitat en la resposta, per
raons que ara no fan al cas, es presentaven d'altres
taules amb un aspecte clar d'homogeneïtat total. Els percentatges
per files coincideixen d'una fila a l'altra i són també
els mateixos que els que podem observar en la distribució marginal
de totals. Aquesta idea és la que serveix per calcular les freqüències
esperades sota la hipòtesi d'homogeneïtat.
- Per calcular les freqüències esperades en cada casella
d'una taula creuada, sota la hipòtesi d'homogeneïtat en
la resposta, es prendran com a dades els totals per files i per columnes
i s'imposarà que, en cada fila, els percentatges per files siguin
iguals que els percentatges de la fila de totals. La taula de freqüències
esperades reprodueix "la situació ideal", la donada per la homogeneïtat
de la resposta d'una variable respecte a l'altra en el conjunt de la
població. El test de khi quadrat serveix, llavors, per mesurar
les discrepàncies entre les freqüències absolutes
observades en la mostra que s'ha estudiat i les freqüències
esperades sota la hipòtesi nul·la (que serà d'homogeneïtat).
A la taula
que hem considerat inicialment es partiria, doncs, de les dades
que hi ha a la taula de l'esquerra.
Podeu calcular els percentatges a la fila de totals, que són:
Aptes, 42,9 %
No aptes, 57,1 %
|
|
Per completar
la taula de freqüències esperades s'imposa que,
en cada fila de la taula "ideal", els percentatges siguin els
que ja s'han comentat. Així, per exemple:
Homes/Aptes:
el 42,9 % de 80, que és 32,3
I així amb les altres caselles
|
| |
Aptes |
No aptes |
Total |
| Homes |
|
|
80 |
| Dones |
|
|
60 |
| Total |
60 |
80 |
140 |
|
|
| |
Aptes |
No aptes |
Total |
| Homes |
34,3 |
45,7 |
80 |
| Dones |
25,7 |
34,3 |
60 |
| Total |
60 |
80 |
140 |
|
Nota: Tot i que les freqüències
esperades, conceptualment (pel fet que són freqüències
absolutes) haurien de ser nombres enters, en l'aplicació del
test de khi quadrat es consideren amb decimals si així resulten
de l'aplicació de la fórmula corresponent.
- Si es formula simbòlicament el que s'acaba de dir, resulta:
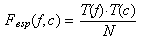 on Fesp(f,c) representa la freqüència
esperada en la casella corresponent a la fila f, columna c;
T(f) el total d'observacions en la fila f; T(c)
el total d'observacions en la columna c, i N el nombre
total d'observacions.
on Fesp(f,c) representa la freqüència
esperada en la casella corresponent a la fila f, columna c;
T(f) el total d'observacions en la fila f; T(c)
el total d'observacions en la columna c, i N el nombre
total d'observacions.
Ara que ja tenim criteris per decidir les freqüències
esperades, ja podríem aplicar una prova de khi quadrat, però
ens falta comentar el nombre de graus de llibertat que caldria considerar.
Si, com succeeix en aquest cas, a partir de les freqüències
observades deduïm un seguit de valors que després emprem per
calcular les freqüències esperades, això fa rebaixar
els graus de llibertat amb què cal aplicar el test.
En aquest cas, s'han emprat:
- El nombre total de dades (que ja sabem que sempre fa rebaixar
en 1 el nombre de graus de llibertat).
- Els totals de cada fila, però d'aquests totals només
són independents tants com files hi hagi menys 1 (perquè
la suma de tots aquests totals és el nombre d'observacions).
- Els totals de cada columna, però d'aquests totals també
només són independents tants com columnes hi hagi menys
1 (perquè la suma de tots aquests totals és el nombre
d'observacions).
Així, si indiquem per m el nombre de files i per n
el nombre de columnes (sense comptar la fila i columna de totals), el nombre
de classes és m · n, de les quals s'han de restar,
pel total de dades, 1; pels totals de files, m – 1, i pels totals
de columnes, n – 1, i obtindrem finalment:
- El nombre de graus de llibertat amb què cal aplicar
la prova de khi quadrat en l'anàlisi d'una taula de doble entrada
és: m · n – 1 – (m –
1) (n – 1) = (m – 1) · (n –
1).
- A la pràctica 3 veurem l'aplicació
d'aquest test mitjançant el programa Excel a alguns exemples.
No cal fer consideracions teòriques com les anteriors ni en molt
casos calcular efectivament les freqüències esperades; n'hi
ha prou amb saber interpretar els resultats que ens doni el programa.
Això sí, seguidament examinem manualment la conclusió
de l'exemple que hem fet servir que, recordeu-ho, adopta un punt de
vista diferent al que és habitual quan es fa servir l'ordinador.
- Suposem que volem aplicar la prova amb un nivell de significació
del 5 %.
- Hipòtesi nul·la: homogeneïtat en la resposta.
- Freqüències observades: les donades per les quatre caselles;
40, 40, 20, 40.
- Freqüències esperades: les que s'acaben de calcular:
34,3; 45,7; 25,7; 34,3.
- Càlcul de l'estadístic X2:
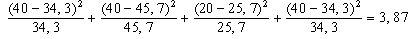
- Hem de consultar la taula de regions crítiques
de khi quadrat en el benentès que ara s'ha d'aplicar la prova
amb 1 grau de llibertat
[m = 1, n = 1, graus de llibertat (m – 1)
· (n – 1)].
- Llegirem el valor 3,84 a la casella corresponent. Com que el valor
3,87 de l'estadístic X2 ultrapassa el valor
que ens dóna la taula (però per ben poc), amb el nivell
de significació del 5 % podem rebutjar la hipòtesi d'homogeneïtat.
- Adoneu-vos, però, a la vista de la taula, que si es treballés
amb més rigor i toleréssim un risc màxim d'error
del 2,5 %, no es podria rebutjar la hipòtesi d'homogeneïtat,
sinó que podríem admetre que les diferències
observades són fruit de l'atzar (i això per a la taula
inicial, independentment de les altres consideracions ja comentades
al mòdul 3).
- El punt de vista que es presenta a les pràctiques, amb l'ús de l'Excel, ens diu
fins a quin nivell de significació es podria admetre l'homogeneïtat
i acceptar que les diferències observades entre sexes són
fruit de l'atzar.
|
| |
|
 |
Prova d'independència |
| |
|
| |
L'exemple de l'apartat anterior considerava
una variable de classificació o variable explicativa i una variable
de resposta. El tractament formal que es feia a l'una i l'altra no era pas
simètric. És clar que un plantejament invers no tindria sentit. No
és possible un tractament simètric de les dues variables.
Podem pensar que ser admès o no en una facultat pot tenir influència
sobre el sexe?
Tanmateix, en moltes altres ocasions convé estudiar les relacions
entre variables anàlogues, sense que es pugui veure una d'elles
com a resposta d'una altra. Això passaria, per exemple, si estudiéssim
la relació entre les notes qualitatives de català i de castellà
d'un conjunt d'alumnes. No sembla adequat pensar que unes qualificacions
són resposta de les altres, sinó que pot interessar constatar
si es manifesta un grau d'associació significatiu. En cas contrari,
es pot dir que les variables estudiades són independents.
Aquesta anàlisi es fa també amb un test de khi quadrat.
En aquest cas, s'adopta com a hipòtesi nul·la H0:
la independència de les variables en la població considerada
i per calcular les freqüències esperades amb aquest enfocament
s'adopta un punt de vista probabilístic. Recordeu que:
- Es diu que dos esdeveniments A i B són independents
si i només si:
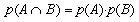
En aquest cas, si suposem que hi ha independència entre les variables
(com correspon a la hipòtesi nul·la d'ajust al model que ara
interessa) resulta que la probabilitat que un individu de la mostra pertanyi
a una casella (fila f, columna c) ha de ser igual a la probabilitat
de pertànyer a la fila f multiplicat per la probabilitat de
pertànyer a la columna c.
Pel que fa a la probabilitat, cal estimar els valors
que prendrem com a tals a partir de les freqüències relatives
que es dedueixen dels totals marginals obtinguts a partir de les dades.
- Si representem per T(f) el total d'observacions a la
fila f; per T(c) el total d'observacions a la columna
c, i per N el nombre total d'observacions, podem escriure:
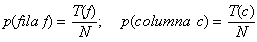
- Llavors, sota la hipòtesi nul·la d'independència,
la probabilitat p(f,c) de pertànyer a la casella
corresponent a la fila f i la columna c s'obté
multiplicant les dues anteriors i és:
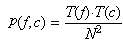
- Per tant, la freqüència esperada en cada casella, Fesp(f,c),
que s'obté multiplicant la probabilitat de pertànyer a
la casella pel nombre total de dades observades, és, com en el
cas del test d'homogeneïtat:
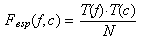
Observem, doncs, que tot i que el plantejament inicial teòric ha
estat diferent del que hem fet a l'apartat anterior, les freqüències
esperades són les mateixes. Com que per calcular les freqüències
esperades fem servir els mateixos totals (de dades, per files i per columnes)
que en el cas anterior, també coincideix el nombre de graus de llibertat
amb què cal aplicar la prova de khi quadrat.
No hi ha, doncs, cap diferència en l'aplicació pràctica
del test. Allò que varia és el comentari que podem fer a
la vista de les variables estudiades i del paper que juguen unes respecte
a les altres. Acabarem aquest document amb un exemple didàctic
(no hi busqueu la finalitat estadística) de l'aplicació
de la prova des d'un punt de vista manual. Com que no sempre es disposa
de l'ordinador, també convé conèixer aquest procediment,
que és diferent del que cal adoptar quan es treballa amb l'Excel.
Exemple
La taula següent dóna el color dels
ulls (foscos, verds o blaus) i l'alçada classificada en dues categories
(alts i baixos) d'una mostra de 100 individus extreta d'una determinada
població. Volem estudiar si, a partir de la mostra recollida, es
pot pensar que hi ha relació entre aquests caràcters en la
població estudiada.
| |
Fosc |
Verd |
Blau |
Total |
| Alts |
23 |
9 |
8 |
40 |
| Baixos |
35 |
16 |
9 |
60 |
| Total |
58 |
25 |
17 |
100 |
En aquest cas, cal fer un tractament simètric de les dues variables
estudiades. Per calcular les freqüències esperades, es parteix
de la taula de l'esquerra, des de la qual, amb la fórmula ja indicada,
es poden calcular les freqüències esperades sota la hipòtesi
d'independència que el test ens ha d'ajudar a contrastar. La taula
de freqüències esperades es transcriu a la dreta:
| |
Fosc |
Verd |
Blau |
Total |
| Alts |
|
|
|
40 |
| Baixos |
|
|
|
60 |
| Total |
58 |
25 |
17 |
100 |
|
|
| |
Fosc |
Verd |
Blau |
Total |
| Alts |
23,2 |
10,0 |
6,8 |
40 |
| Baixos |
34,8 |
15,0 |
10,2 |
60 |
| Total |
58 |
25 |
17 |
100 |
|
D'un cop d'ull ja veiem que hi ha molta semblança entre les freqüències
observades i les freqüències esperades en cas d'independència,
cosa que ens porta a pensar que podem mantenir la hipòtesi nul·la.
No hi ha criteris amb aquesta mostra per rebutjar-la.
Com ho hem de fer amb el test de khi quadrat?
- Calculem l'estadístic X² i resulta
ser, en aquest exemple, de 0,52.
- El test s'aplica amb 2 graus de llibertat
(m = 2, n = 3, (m – 1) · (n –
1) = 2). En aquest cas (vegeu taula), la regió
crítica amb un nivell de significació del 5 % està
definida pel valor 5,99.
- Com que el valor observat és molt
més petit (molt i molt!) que el que determina la regió
crítica, no hi ha criteris amb les dades d'aquesta mostra per
rebutjar la hipòtesi nul·la.
- Conclusió: en la població estudiada no
hi ha cap relació entre l'alçada i el color dels ulls,
es tracta de variables independents.
És clar que, a més de saber fer els càlculs per aplicar
la prova de khi quadrat i interpretar els nombres que surten, abans que
res cal analitzar la consistència d'un estudi estadístic,
cosa que ja s'ha dit que no era pas la finalitat del darrer exemple. |
| |
|
| |
|
 |
| |
|