Una vegada coneguts els termes relacionats amb els contrastos estadístics (molt especialment el significat del valor p) en aquesta pràctica, que es pot considerar d'ampliació, es presenten diverses proves útils en la valoració de la significació d'hipòtesis sobre mitjanes.

Es tracta de respondre a preguntes del tipus "allò que s'observa en aquest conjuntés significativament millor que la mitjana de la població?", o bé "les notes del grup A indiquen que aquest grup és significativament millor que el grup B?" o, encara, "el repàs que hem fet d'un tema de coneixements bàsics, ha comportat un augment significatiu en el rendiment en les proves de control?".

Tot i que els elements estadístics que hi ha al darrere de les proves escapen dels objectius del curs, com que les proves es poden fer ràpidament amb el programa Excel, ha semblat interessant comentar-les. L'objectiu fonamental d'aquestes proves és quantificar si unes diferències observades permeten dubtar significativament de la hipòtesi nul·la "conservadora" que estableix que s'ha de mantenir el model. Ha semblat interessant ressaltar la idea que el que es valora és el nivell de significació d'unes diferències observades. És clar, si no observem diferències ja no farem cap prova!

Els temes concrets que es tractaran són els següents:

• Proves de contrast de la mitjana d'una mostra enfront de la mitjana de la població.
• Proves de comparació de mitjanes de dues mostres.
• Proves de comparació de mitjanes de dades emparellades.
• Un comentari sobre què representa l'ANOVA (anàlisi de la variància).

Les primeres proves que presentem tenen l'objectiu de contrastar una mitjana.

La situació és la següent: es recullen dades d'una variable contínua sobre una mostra, i alhora se sap un model que permet conèixer la mitjana d'aquella variable en la població. La prova intenta establir si hi ha criteris per decidir que la mostra és significativament diferent del conjunt de la població.

Per exemple, quan el DURSI envia al nostre centre la mitjana de la nota que han tret els nostres alumnes de matemàtiques a les PAU i envia també la nota mitjana de Catalunya, podem aplicar aquestes proves per veure si les diferències observades són significatives o no.

Veureu que hi ha dos plantejaments teòrics segons quina sigui la informació de què disposem pel que fa a les dades de la població. Aquests plantejaments teòrics poden ser fruit de condicionants pràctics o d'un altre tipus.

La primera de les proves, prova z per a una mostra, és un test inferencial sobre la mitjana que es fa, suposada coneguda la mitjana i la desviació estàndard de la població. La hipòtesi nul·la, en aquest cas, és que la mitjana del conjunt on s'ha pres una mostra és igual a la mitjana de la població. A partir dels comentaris que hem fet, ja podeu entendre que és igual vol dir no tenim criteris per suposar, de manera significativa, que és diferent.

En aquesta prova es calcula l'estadístic , en què és la mitjana de la mostra, µ, la mitjana i la desviació estàndard de la població, i n la mida de la mostra (nombre de dades).

La distribució d'aquest estadístic és la distribució normal estàndard, habitualment representada com a Z i d'aquí la denominació de la prova.

Exemple 1: Rebem una informació estadística de l'Oficina de Coordinació de les PAU que ens diu que a les proves de selectivitat d'enguany la mitjana de l'examen de matemàtiques ha estat 4,98 amb una desviació estàndard d'1,72. Les notes dels nostres 28 alumnes han estat les següents:

4,5   5,5   6,0   8,0   7,5   10    1,5   0,5   3,5   6,5
0,5   4,5   4,5   5,5   6,5   5,0   7,5   8,5   3,5   9,5
9,5   7,0   4,5   3,5   2,5   6,5   5,5   0

Es pot dir que el rendiment d'aquest grup d'alumnes, que han tingut una mitjana superior a la de Catalunya, ha estat significativament millor que la població sencera?

Aquesta és la pregunta que podem respondre amb la prova de z-per a una mostra. Vegem com la podem aplicar amb l'Excel.

• Entreu aquestes notes en una columna d'un full de càlcul nou. Suposem que el rang que heu fet servir és A2:A29, perquè a A1 hi teniu un rètol.
• Calculeu la mitjana. Entreu la fórmula =PROMEDIO(A2:A29) a la cel·la B2. Així veureu que a ull la mitjana de la mostra és força més gran que la de la població.
• Entreu a la cel·la D2 la fórmula =PRUEBA.Z(A2:A29;4,98;1,72), amb el benetès, com sempre, que si voleu entendre bé què és cada argument, podeu fer Insertar | Función i triar la funció PRUEBA.Z. Aquesta fórmula calcula el valor p de la prova z per a unes dades que estan en el rang A2:A29, amb una mitjana de la població = 4,98 i una desviació estàndard de la població = 1,72.

Veureu que la conclusió del test, valor p gran, no ens permet dubtar significativament de la hipòtesi nul·la (que, com ja hem dit, és mitjana de la mostra = mitjana de la població). Tot i que observem una mitjana força més gran que la teòrica de la població, hem d'entendre que la diferència pot ser fruit de l'atzar. En la conclusió hi influeix el fet que la mostra és poc nombrosa.

Podeu veure que, si canvieu el valor 4,98 de la mitjana de la població per 4,68, llavors el valor p de la prova esdevé molt petit. Si fos aquesta la dada coneguda, no tindríem gairebé cap risc de rebutjar la hipòtesi nul·la. Llavors sí que podríem anunciar: "Els nostres alumnes de matemàtiques són significativament millors que la mitjana de Catalunya". Feu la prova i vegeu que si aneu abaixant la hipotètica mitjana de la població, cada vegada el valor p és més petit.

Com que la desviació estàndard no se suposa coneguda, ara es calcula l'estadístic , en què i s representen la mitjana i la desviació estàndard de la mostra, µ la mitjana teòrica de la població i n la mida de la mostra.

La diferència amb el cas anterior és que s'estima la desviació estàndard de la població a partir de s, desviació estàndard del conjunt de dades que formen la mostra. El model teòric per a la distribució mostral de l'estadístic és la distribució t de Student, que dóna nom a la prova, prova t per a una mostra. Compareu la situació anterior amb la següent:

Exemple 1 bis: Llegim a la premsa una notícia que ens diu que a les proves de selectivitat d'enguany la mitjana de l'examen de matemàtiques ha estat 4,98 i vistes les notes dels nostres 28 alumnes, que ja hem indicat anteriorment i que donen una mitjana de 5,286, pensem que potser han estat significativament millors (de mitjana, és clar).

Com ho podem decidir amb l'Excel?

• Vist el nom de la prova, potser pensareu que es tracta de buscar la funció PRUEBA.T (que trobem a la llista de funcions). Però no és així, sinó que cal fer servir la mateixa funció PRUEBA.Z d'abans, però sense el darrer argument.
• Llavors la fórmula =PRUEBA.Z(A2:A29;4,98) ens ajudarà a respondre la pregunta amb el benentès que partim d'una situació amb menys informació que la comentada anteriorment. Vegeu que si obriu el quadre de diàleg per inserir aquesta funció, quan us situeu al requadre del tercer argument diu: Sigma: es la desviación estándar (conocida) de la población. Si se omite, se usarà la desviación estándar de la muestra, cosa que concorda del tot amb l'explicació que hem donat.
• Podeu veure que la conclusió inicial del test és anàloga a l'anterior.
• Però, tanmateix, si aneu fent proves sobre hipotètiques mitjanes de la població, veureu que:
  • Si fos 4,68, en aquest cas on tenim menys infromació que abans (desviació estàndard desconeguda), encara no seria prou significativa la diferència.
  • Si aneu fent proves, podeu veure que, si volem treballar amb un nivell de significació del 5 %, la mitjana de la població hauria de ser de 4,43 per poder dir que la nostra mitjana de 5,286 amb 28 alumnes és significativament diferent.

Com la darrera que hem vist, el nom de proves t els ve del fet que els estadístics que s'estudien corresponen al model donat per la distribució t de Student.

Prsentareu l'estudi amb l'Excel mitjançant la funció PRUEBA.T. Podeu veure que a Herramientas | Análisis de datos també hi ha incloses les proves que veureu en aquest apartat i al següent, però, tanmateix, s'ha optat per la via indicada, perquè la sortida de resultats se situa en un marc molt més concret: ens dóna simplement el valor p que ens permet treure la conclusió que volem, amb el benentès que la hipòtesi nul·la estableix la igualtat de mitjanes. Necessitem proves fefaents (un valor p molt baix) per dubtar del model establert i considerar significatives les diferències de valors observades.

Exemple 2: Després d'analitzar les notes dels nostres alumnes a les PAU, que hem vist a l'exemple anterior, ens assabentem de les notes obtingudes a la mateixa prova pel conjunt d'alumnes d'un institut proper; com a infromació suplementària sabem que els correctors han estat diferents.

3,4    3,5    5,3    5,4    5,1    7,9    7,6    3,2
7,8    5,4    7,6    7,8    3,5    5,4    7,2    7,3
3,8    5,7    7,8    7,5    3,6    5,7    5,8    7,3
3,7    5,9    7,0    3,6    7,5    3,1    7,3    7,9

• Poseu un rètol a la columna B del full on teniu les notes de l'exemple 1 i entreu les notes de l'altre institut al rang B2:B33.
• Calculeu les dues mitjanes. Veureu que una és de 5,286 i l'altra de 5,831. La PRUEBA.T ens dirà si la diferència és significativa o no.
• Escriviu en una cel·la lliure la fórmula =PRUEBA.T(A2:A29;B2:B33;1;2). Ja veieu que els dos primers arguments que s'entren a la funció són els dos rangs on tenim les dades que configuren les dues mostres. Els altres arguments es comentaran més avall.
• El resultat que ens dóna la funció anterior és el valor p de la prova t per a dues mostres. És un valor p força alt.
• Conclusió: la diferència de mitjanes observada no és prou significativa per dubtar de la hipòtesi nul·la que, en aquest cas, estableix que les dues poblacions de partida són estadísticament equivalents.

El quadre de diàleg que apareix quan es fa Insertar | Función | PRUEBA.T és el següent:

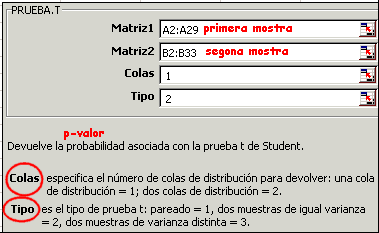
Podeu veure de seguida que al tercer requadre se'ns demana el nombre de cues amb què es vol aplicar la prova. Aquest fet concorda amb el fet que en algunes proves d'hipòtesis convé proposar una hipòtesi alternativa, que és la que interessa acceptar en cas de rebutjar la hipòtesi nul·la.

Recordeu que a la prova que ara estudiem la hipòtesi nul·la és Igualtat de mitjanes de les poblacions. Una formulació de la hipòtesi alternativa és Les mitjanes de les poblacions són significativament diferents, però, en canvi, en la majoria de situacions pràctiques, interessa més una formulació del tiups La mitjana de la segona població és significativament més gran que la mitjana de la primera. La primera d'aquestes formulacions es diu una prova de dues cues, i la segona formulació (la que els autors aconsellen en tots els exemples que presenten) és una prova d'una cua. Aquesta consideració té relació amb el resultat que s'obté per al valor p i també enllaça amb un concepte anomenat la potència d'un test:

El darrer argument de PRUEBA.T fa referència al Tipo de prueba i enllaça amb el fet que aquesta prova té diverses versions que s'apliquen en situacions conceptualment diferents. A part de la de dades emparellades, que es comenta a l'apartat següent de la pràctica, la prova t per a dues mostres independents també té dos plantejaments teòrics diferents: un d'ells treballa amb la hipòtesi es poden suposar variàncies iguals per a les poblacions (o subpoblacions) on s'han recollit les dades de les dues mostres, i en l'altre plantejament aquesta assumpció no es pot fer.

Convé comentar l'existència d'aquestes dues situacions tot i que, pels objectius i les possibilitats del curs, segurament n'escapa el plantejament teòric de cada cas. Heu de saber que hi ha una prova de contrast que permet contrastar numèricament la plausibilitat de la suposició d'homogeneïtat de les variàncies.

• L'experiència pràctica ensenya que si les dues mostres tenen, si fa o no fa, la mateixa mida, l'aplicació de la PRUEBA-T per a dues mostres amb la hipòtesi d'homogeneïtat de variàncies o sense aquesta hipòtesi dóna molt poca diferència en els valors p. Vegeu que si escriviu =PRUEBA.T(A2:A29;B2:B33;1;3) en lloc de =PRUEBA.T(A2:A29;B2:B33;1;2) la diferència és ben petita. Si heu vist l'ampliació, sabreu quina de les dues opcions és estrictament més correcta, però l'una i l'altra ens fan acceptar la mateixa conclusió.

Exemple 3:
Analitzarem tot seguit les dades contingudes al full Paujuny del llibre PAU.XLS.

1. Hi ha diferències significatives entre les notes de català i de castellà?
2. I entre les de català i les d'anglès?
3. Hi ha diferències significatives en el rendiment de les notes de català entre els alumnes de ciències (opcions 1 i 2) i els de lletres (opcions 3 i 4)?

Vegem com s'arriba a les respostes.

1. Amb la fórmula =PRUEBA.T(B2:B62;C2:C62;1;2). Conclusió: no hi ha diferències significatives.
2. Amb la fórmula =PRUEBA.T(B2:B62;F2:F62;1;2). Conclusió: sí que hi ha diferències significatives.
3. Tot i que aquest tipus de preguntes (diferència de mitjanes entre subpoblacions) és molt usual en situacions pràctiques, l'Excel no incorpora un procediment directe per respondre-les. S'explica tot seguit.

• Accediu al llibre PAU.XLS i inseriu-hi un full nou.
• Obriu el full Paujuny i seleccioneu la columna A. Activeu Datos | Autofiltro.
• Amb el desplegable d'Opció seleccioneu 1. Seleccioneu les dades que ara apareixen a la columna LLC i feu Control + C.
• Obriu el full nou que heu inserit i a la columna A, poseu-hi el rètol Cata-1 i llavors feu Edición | Pegado Especial | Valores i enganxeu a partir de la cel·la A2 les dades que teniu a punt per copiar.
• Repetiu-ho amb les dades corresponents a les categories definides per les opcions 2, 3 i 4. Veureu que al full nou teniu dades numèriques als rangs A2:A18, B2:B15, C2:C9, D2:D23.
• Podeu veure que la mitjana de les notes corresponents a les opcions 3 i 4 és més gran que la mitjana de notes de les opcions 1 i 2. En concret, 5,7 enfront de 4,8. És molt més gran? És força més gran? La pregunta, des del punt de vista estadístic és: És significativament més gran?
• Ara ja podeu aplicar la PRUEBA.T, que és prou flexible pel que fa als rangs on hi ha les dades i, per altra banda, no té en compte cel·les en blanc.
  Per fer el contrast entre el conjunt d'alumnes de les opcions 1 i 2 i el conjunt d'alumnes de les opcions 3 i 4, escriviu =PRUEBA.T(A2:B18; C2:D23;1;2) i ja estareu a punt per treure'n una conclusió.

Com que esteu "lluitant" contra la hipòtesi nul·la que indica que no es pot pressuposar diferència significativa de mitjanes i, en canvi, heu observat un valor p molt petit, la conclusió que podeu treure és que la diferència de mitjanes és significativa.

En altres programes estadístics, es permet entrar com a dades per a l'aplicació de la
prova t una columna on hi ha els valors numèrics observats i una altra on tenim els valors d'una variable de classificació. En aquests casos, com en el que acabem d'examinar, la prova tendeix a contrastar diferències significatives entre les mitjanes observades en les subpoblacions. Aquest mateix plantejament obre la porta d'un camp de treball de l'estadística que es coneix com a ANOVA (anàlisi de la variància), però que en bona part és una prova de contrast de mitjanes entre subpoblacions.

En aquest tipus de situacions, també hi té el seu àmbit d'aplicació la PRUEBA.T de l'Excel.

Abans de passar a un exemple pràctic, és important reflexionar sobre el fet que les proves de dues mostres que hem vist fins ara fixaven l'atenció en la globalitat de les observacions en cada mostra, independentment les unes de les altres. En canvi, ara veureu una prova que tracta les dades d'una mostra i de l'altra no de manera independent, sinó emparellades.

Més que una prova de dues mostres, doncs, seria més encertat dir que farem una prova per a una mostra bivariant, i l'estudi que es fa, doncs, es pot complementar en certa manera amb un estudi de la correlació i la regressió lineal.

Exemple 4: Estudiareu les dades incloses en el llibre MATE1.XLS del qual podeu llegir la descripció detallada. Ara fixareu l'atenció en les variables NOTA1, NOTA2 i NOTA3 que corresponen a les qualificacions en:

• Una prova inicial de coneixements mínims.
• Una prova anàloga plantejada en acabar un repàs exhaustiu (aquest repàs exhaustiu seria el tractament o l'experimentació estadística).
• Una tercera prova anàloga feta quatre mesos després de l'anterior, quan ja es treballaven altres temes.

• Obriu el llibre indicat, que només té el full Notes bup 1. Escriviu en una cel·la lliure la fórmula =PRUEBA.T(C2:C40;D2:D40;1;1) on consten els rangs als quals tenim les notes que volem considerar; el primer 1 indica que volem fer una prova d'una cua (perquè el que volem constatar és si el tractament ha fet millorar les notes, no ens basta -ni tindria gaire sentit- veure si les ha modificat); i finalment, el darrer 1, que hem destacat de manera especial, explica que volem fer una prova de dades emparellades.
• Veureu un valor p extraordinàriament petit. No hi ha cap dubte que podem rebutjar la hipòtesi nul·la i que, per tant, la millora observada ha estat estadísticament significativa.

Segona qüestió: Va ser realment eficaç el plantejament didàctic? Atenent a la idea que interessava que l'alumnat sabés sempre aquestes qüestions operatives bàsiques, era cert, això, quan ja no es treballaven els temes explícitament?

• Feu =PRUEBA.T(C2:C40;E2:E40;1;1). Veureu que el valor p ja ha augmentat una mica, però encara és molt baix; sí que tenim arguments que indiquen que el "tractament" va servir perquè l'alumnat millorés significativament a la llarga.

Per acabar, insistim que aquesta versió de la prova analitza la informació molt més a fons que un simple contrast de mitjanes com els que hem vist a la segona part de la pràctica. No solament mirem si el grup, com a col·lectiu, va millorar, sinó que hem fet un experiment del tipus mesura abans --> tractament --> mesura després i hem estudiat el comportament alumne per alumne (dades emparellades)

És interessant comentar que la fonamentació teòrica d'aquestes proves que ara es presenten i la del problema d'estimació de la mitjana d'una població tenen certa similitud, però adopten punts de vista diferents.

• En aquesta pràctica, se suposen conegudes les característiques d'una població i les proves de contrast intenten establir si els valors observats en una mostra han estat recollits en un conjunt que es pot considerar significativament diferent de la globalitat de la població.
• En el mòdul següent, la situació és, en certa manera, inversa: a partir dels valors recollits en una mostra, que se suposa representativa d'una població, s'intenten estimar les característiques globals d'aquella població.

Ambdues situacions es basen en l'estudi de la variabilitat de l'estadístic mitjana mostral que s'estudia a bastament al mòdul següent.

Si el model de la població (en particular la mitjana) és conegut i l'interval de confiança per a l'estimació de la mitjana conté el valor conegut d'aquesta dada, no podem dubtar significativament d'aquell model.

Per aplicar una versió o l'altra de la prova-t per a dues mostres, cal basar-se en la plausibilitat o no d'un model donat per variàncies iguals en els dos processos de recollida de dades.

L'Excel incorpora una prova estadística que permet contrastar el grau de significació d'aquesta hipòtesi. Per aplicar aquesta prova, cal tenir les dues mostres en rangs diferents i llavors la manera més ràpida és fer servir la funció PRUEBA.F, a la qual hem d'entrar com a arguments els dos rangs on tenim una mostra i l'altra i ens retorna el valor p de la prova que pren com a hipòtesi nul·la la homogeneïtat de les variàncies.

• Amb les dades de l'exemple 2 de la pràctica (notes de les PAU de dos instituts diferents), aquesta prova s'aplicaria així: =PRUEBA.F(A2:A29;B2:B33). Obtenim un
  valor p molt petit. Conclusió: no podem basar-nos en l'homogeneïtat de variàncies. Des d'un punt de vista pràctic, això podria voler dir que els dos correctors que han valorat un centre i l'altre tenen mètodes de valoració diferents, cosa que no vol pas dir que un puntuï més alt que un altre, sinó diferent, amb molta més variabilitat l'un que l'altre.

• Pel que fa a l'exemple 3 que es comenta a la pràctica, en les dades del llibre PAU.XLS s'observa homogeneïtat en la variància pel que fa a les notes obtingudes en les diverses matèries?
  • Obriu l'esmentat llibre.
  • Escriviu en una cel·la buida =PRUEBA.F(B2:B62; C2:C62). Veureu que surt un
    valor p molt alt. La conclusió és que no es pot dubtar de la hipòtesi d'homogeneïtat de la variància entre el corrector de català (LLC) i el de castellà (LLE).
  • El mateix passa amb tots els parells de matèries. No sempre els valors p són tant alts; de vegades s'acoten al 5 % i ens podrien fer dubtar una mica si treballem amb aquest nivell de significació.
  • En canvi si escriviu =PRUEBA.F(B2:B62; K2:K62), veureu un valor p molt i molt petit. Així, doncs, no hi ha homogeneïtat en la variància en les qualificacions de català de les PAU i les notes de l'expedient, les que tenim a la variable Llibre.
  • Com en l'exemple anterior, convé no confondre aquest fet amb l'afirmació que unes qualificacions són millors que les altres. La plausibilitat de l'homogeneïtat de les variàncies és una hipòtesi de treball per a la prova de contrast de les mitjanes, que és la que ens permet dir si un conjunt de dades és significativament diferent de l'altre o no.

Pareu atenció a les diferents situacions que es poden donar en un contrast d'hipòtesis estadístiques:

	Hipòtesi nul·la certa	Hipòtesi nul·la no vàlida Alternativa correcta
S'accepta H0	Decisió correcta	Decisió errònia Error de tipus II
Es rebutja H0	Decisió errònia Error de tipus I	Decisió correcta

Ja hem comentat en el document de fonaments Els contrastos d'hipòtesis que, de les dues decisions errònies, es considera conceptualment molt més seriosa la que ens fa rebutjar H₀ quan de fet és certa. Habitualment, una decisió d'aquest tipus rep el nom d'error de tipus I.

A partir d'aquesta idea, recordeu que el valor p dóna la probabilitat de caure en un error del tipus I i ens permet determinar el nivell de significació del test.

Fixeu-vos ara en l'altra decisió errònia que es pot prendre: no encertar a rebutjar H₀ i donar validesa a la hipòtesi alternativa quan, de fet, això seria el que escauria.

És per això que s'introdueix el concepte de potència d'un test que mesura la capacitat d'encert del test.

Es defineix com a potència d'un test la probabilitat que, en un contrast d'hipòtesi, s'encerti a rebutjar la hipòtesi nul·la quan efectivament és falsa i, consegüentment, s'accepti la hipòtesi alternativa.

Tanmateix, s'ha de considerar que moltes vegades la hipòtesi alternativa no és tan concreta com la hipòtesi nul·la, i pot costar descobrir-la. Per exemple, si la hipòtesi nul·la és mitjana=0, aquesta afirmació és molt més concreta, per exemple, que mitjana > 0. Pot ser que la mitjana, de fet, sigui molt poc diferent de 0, el test no encerti a descobrir-ho i cometem un error del tipus II. Per això, un mateix test encaminat a contrastar el valor d'un paràmetre estadístic té diferents valors de la potència, un per cada possible valor del paràmetre que faci vàlida la hipòtesi alternativa; de fet, doncs, el concepte de potència ens porta a definir una funció, i el seu gràfic es coneix com a corba de potència del test.
 

Es pot dir, en una primera visió intuïtiva, que les tècniques estadístiques conegudes com a ANOVA (anàlisi de la variància) generalitzen la prova t quan s'aplica al contrast de les mitjanes de dues subpoblacions, en el cas en què es vol estudiar globalment la variació de les mitjanes entre grups diversos d'una població donats per una variable categòrica.

De fet, en aquesta primera passada, es pot dir que seria més encertat designar aquest estudi com a anàlisi de la variació de les mitjanes entre grups. Es constata que, sovint, el fet que hi hagi més de dos grups fa que les variacions observades d'un grup a un altre o dintre de cada grup no siguin tan importants estadísticament com si només s'analitzessin dos grups.

• Recupereu el full nou que heu obert en el llibre PAU.XLS on teniu les dades de les notes de català (LLC) desapilades en quatre columnes, una per cada opció.

• Feu Herramientas | Análisis de datos | Análisis de la varianza de un factor. Estudiareu la significativitat de les diferències de mitjanes observades en les quatre categories definides pel factor Opció.
  

• Vegeu la sortida d'informació que explica:
  • Que s'han analitzat els quatre grups.
  • Que s'ha estudiat la variació entre grups i dintre de cada grup (aquí és on té un paper important la variància).
  • Que s'ha calculat un estadístic F, del qual se'ns dóna una Probabilitat (que vol dir un valor p) que, en el cas que ens ocupa, és (relativament) gran.

Quina era la hipòtesi nul·la? Que les quatre mostres procedien de subpoblacions que es podia pressuposar que tenien la mateixa mitjana.

Quina conclusió traiem de l'ANOVA que hem tret en pantalla? Que la hipòtesi nul·la té un alt grau de significació; no la podem rebutjar.

Es podria pensar que aquest resultat és contradictori amb el que hem vist sobre les mitjanes de lletres i de ciències. Però no es així: el fet de considerar quatre grups aporta informació totalment diferent en el cas en què considerem només dos grups. Podeu provar de fer únicament dues columnes, enganxant la 1 amb la 2, i la 3 amb la 4, i fer una ANOVA només amb dos grups, i veureu que, en aquest cas, la conclusió és ben bé la mateixa que amb la prova t de dues mostres.