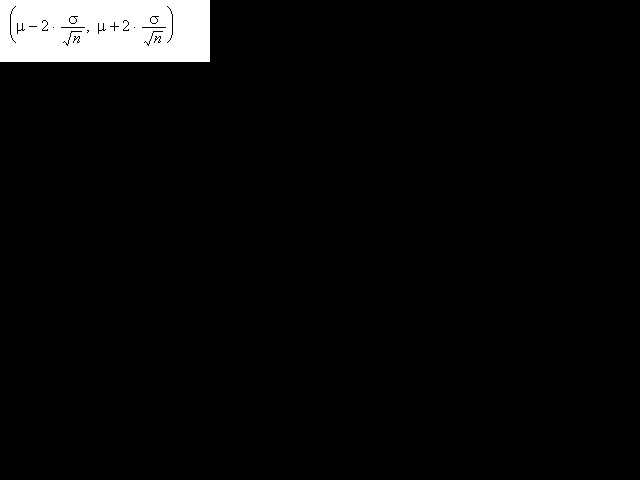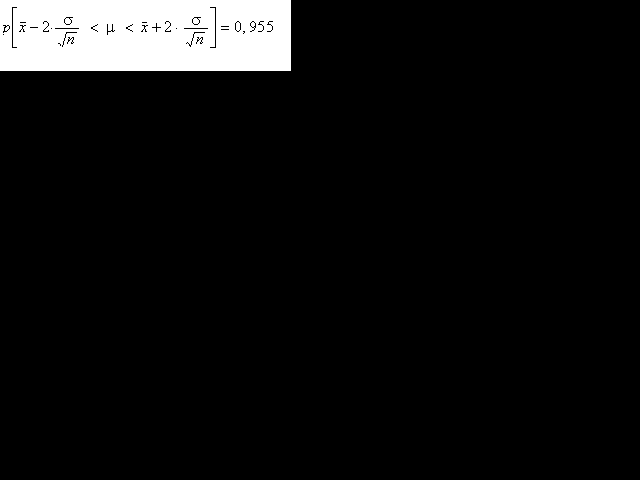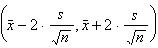|
|
El teorema del límit central. Estimació d'una mitjana

Com el títol ja indica ben clarament, l'objectiu d'aquest document
és presentar des d'un punt de vista conceptual i teòric el teorema
del límit central i, encara que llavors calgui invertir el plantejament
de la situació, veure la seva aplicació per a la deducció
de la fórmula que dóna l'interval de confiança per
a l'estimació d'una mitjana..
Abans de començar la lectura d'aquest resum teòric sobre
el teorema del límit central (o bé en lloc de la reflexió
teòrica) us aconsellem fer la pràctica
4 que en dóna una visió intuïtiva.
|
| |
|
|
|
La variabilitat de la mitjana mostral: teorema
del límit central |
| |
|
|
|
Per tal de decidir el comportament d'un estimador, convé fer "al
laboratori" moltes simulacions que posteriorment es completen amb les
deduccions teòriques necessàries.
El teorema del límit central explica el comportament de l'estadístic
mitjana de la mostra quan prenem mostres aleatòries d'una població
i estudiem els valors que pren en aquesta mostra una variable numèrica.
Veurem que, a partir d'aquest teorema, podrem fer estimacions de la mitjana.
- Teorema: Si partim d'una població en què una
variable X té una distribució normal de
mitjana µ i desviació estàndard s,
i en prenem mostres aleatòries de mida n, l'estadístic
mitjana mostral,
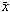 , també segueix una distribució
normal, de mitjana µ i desviació estàndard , també segueix una distribució
normal, de mitjana µ i desviació estàndard
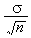 . .
Aparentment, sembla clar (i és cert) que si partim d'una població
qualsevol (i no normal com la del teorema anterior), fins i tot amb una
distribució no coneguda, la distribució de la mitjana mostral
podria ser molt diversa. Tanmateix, empíricament es pot constatar
que no és així, sinó que és correcte un teorema
aproximat, que pot semblar certament sorprenent: si prenem mostres de mida
gran, podem controlar la variabilitat de la mitjana de la mostra a partir
d'una situació qualsevol. Aquest resultat és d'importància
cabdal per a l'estimació de la mitjana d'una població.
Ben segur que aquest fet és un dels que fa que la distribució
normal tingui la importància que té. Hem donat la formulació
del teorema sense la càrrega conceptual i teòrica que té
en les seves versions més potents. Per a la finalitat d'aquest curs,
ens basta aquesta visió intuïtiva i la constatació empírica
que ja heu pogut assolir amb la pràctica
amb l'Excel. Veurem tot seguit que aquest teorema permet fonamentar l'estimació
d'una mitjana.
|
| |
|
 |
Estimació puntual
d'una mitjana |
| |
|
| |
D'acord amb les definicions, per a un estimador
sense biaix, el valor mesurat en una mostra de l'estadístic corresponent
dóna una estimació puntual del paràmetre que
s'estudiï, que sempre ha d'anar acompanyada de l'error estàndard
de l'estimador, és a dir, la desviació estàndard
de la distribució que dóna la variabilitat mostral de l'estadístic.
Tanmateix, en aquesta expressió podem adonar-nos
que el càlcul de l'error estàndard pressuposa que sabem el
valor de la desviació estàndard de la població. No
és massa intuïtiva, aquesta situació, i per això
ens cal donar un criteri per aproximar el valor de l'error estàndard.
La pràctica 5 ensenya que l'estadístic
desviació estàndard mostral corregida (s, o
també sn–1)
és un bon estimador de la desviació estàndard d'una
població.
- Ja sabeu quina tecla d'una calculadora científica ens dóna
el valor d'aquest estadístic? Recordeu també que justament
aquest és el valor que ens dóna l'Excel mitjançant
el procediment ... | Análisis de datos | Estadística
descriptiva amb la denominació desviació estàndard
i amb la funció DESVEST.
Si n és gran (n 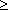 30, cosa imprescindible per poder
considerar vàlida l'aproximació del teorema del límit
central), l'efecte de prendre la desviació estàndard corregida
de la mostra en lloc de la desviació estàndard de la població
(sovint no coneguda) és inapreciable a efectes pràctics. Per
tant, podem enunciar com una bona aproximació la següent: 30, cosa imprescindible per poder
considerar vàlida l'aproximació del teorema del límit
central), l'efecte de prendre la desviació estàndard corregida
de la mostra en lloc de la desviació estàndard de la població
(sovint no coneguda) és inapreciable a efectes pràctics. Per
tant, podem enunciar com una bona aproximació la següent:
- Per fer una estimació puntual de la mitjana µ d'una
variable en una població, mitjançant la selecció
d'una mostra aleatòria de mida n, segons el teorema del
límit central, si n
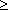 30:
30:
- La mitjana mostral
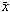 (mitjana dels valors mesurats sobre els elements de la mostra) és
un estimador sense biaix.
(mitjana dels valors mesurats sobre els elements de la mostra) és
un estimador sense biaix.
- Si s és la desviació estàndard corregida
de la variable X en la mostra, es pot prendre com
una bona aproximació de l'error estàndard de l'estimador
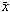 el nombre el nombre 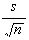 . .
La pràctica 6 mostra els resultats
de l'Excel encaminats a l'estimació d'una mitjana a partir de les
dades d'una mostra.
|
 |
Estimació per interval
d'una mitjana |
| |
|
| |
El coneixement del teorema del límit
central ens permet fer previsions sobre la mitjana mostral (interval de
confiança, o de tolerància) si suposem que partim d'una població
de la qual coneixem la mitjana, µ, i la desviació estàndard,
s, i que la mida de les mostres és
suficientment gran. Recordeu que, en aquest cas:
- La distribució de l'estadístic mitjana mostral és,
aproximadament, normal de mitjana µ i desviació estàndard
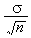 . .
- A partir d'aquest fet, podem dir que la variable que resulta d'estandarditzar
la variable mitjana mostral,
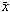 , és a dir, , és a dir, 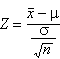 , és aproximadament normal, N(0, 1). , és aproximadament normal, N(0, 1).
Si consultem quin és el valor que defineix l'interval de valors
centrats en la mitjana de probabilitat 0,955 (el 95,5 %) en una distribució
normal N(0,1), podem establir que:
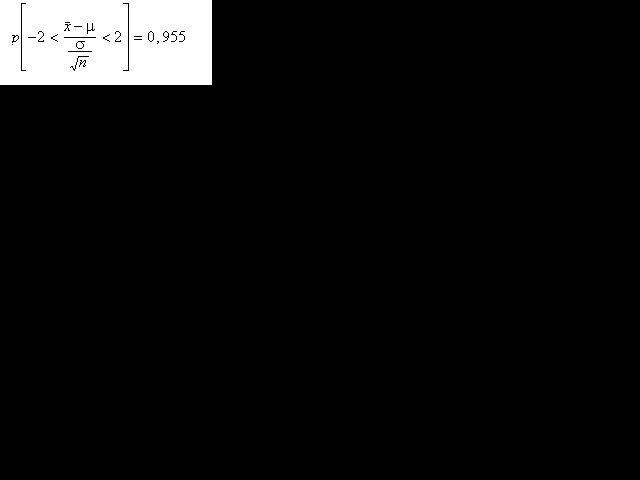 De forma equivalent, podem escriure-ho:
De forma equivalent, podem escriure-ho:
 (#)
I per analogia amb l'estudi de l'estimació d'una proporció
podem enunciar que: (#)
I per analogia amb l'estudi de l'estimació d'una proporció
podem enunciar que:
Si partim d'una població amb mitjana i desviació estàndard
conegudes i fem l'experiència aleatòria consistent a extreure'n
mostres de mida n, l'interval
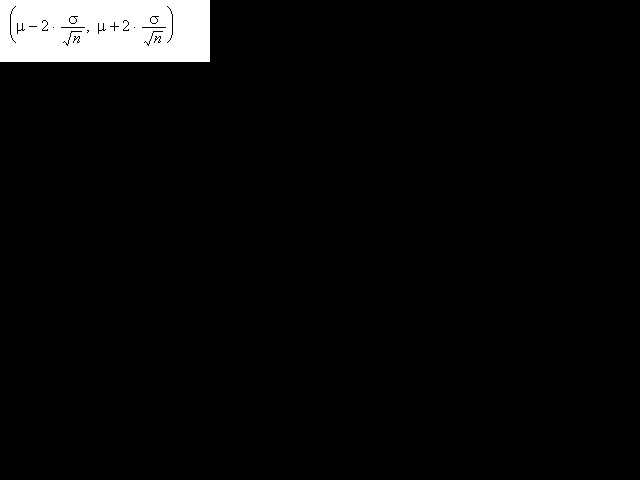 és l'interval de tolerància del 95,5 % per a la mitjana
mostral (anomenat també interval de confiança o de
previsió amb una probabilitat d'encert del 95,5 %).
és l'interval de tolerància del 95,5 % per a la mitjana
mostral (anomenat també interval de confiança o de
previsió amb una probabilitat d'encert del 95,5 %).
Exemple: Entre les persones d'una població la variable
alçada segueix una distribució normal de mitjana
1,652 m i desviació estàndard 0,061 m. Si seleccionem una
mostra aleatòria de 51 persones, quina previsió podem fer
sobre la mitjana de les alçades de les persones de la mostra si
volem tenir una probabilitat d'encert del 95,5 %?
- Per obtenir el radi de l'interval de tolerància cal calcular
2 · 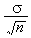 per s
= 0,061 i n = 51. Resulta 0,017. per s
= 0,061 i n = 51. Resulta 0,017.
- Si restem i sumem aquest valor a la mitjana, obtindrem l'interval
(1,635; 1,669) al qual pertany la mitjana mostral amb una probabilitat
del 95,5 %. Aquest és l'interval de tolerància del 95,5
% per a la mitjana mostral (també dit actualment interval
de confiança, com en el cas de l'estimació que comentarem
més avall.
|
|
|
Aquest resultat que acabem d'enunciar també
es pot aplicar a altres situacions que no segueixin una distribució
normal, fins i tot a problemes de probabilitat discrets.
|
| |
Ja hem exposat repetidament que la situació de laboratori que
acabem d'estudiar ens ha de servir per conèixer el comportament de
l'estimador que utilitzem (que en aquest cas és la mitjana mostral),
però la situació pràctica real és la inversa:
- D'una població amb mitjana desconeguda, en seleccionem una
mostra aleatòria i, a partir de les dades d'aquesta mostra, volem
fer una estimació del valor de la mitjana de la variable estudiada
en la població global.
Si manipulem algebraicament l'expressió (#),
arribarem fàcilment a aquesta altra:
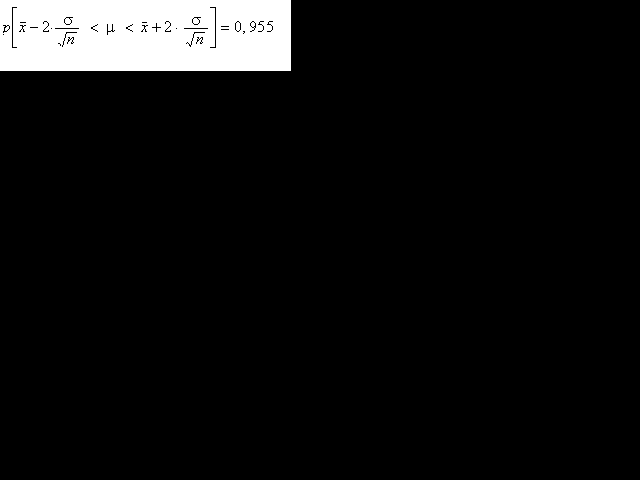 que ens indica que en un mostratge repetitiu la probabilitat que l'interval
aleatori
que ens indica que en un mostratge repetitiu la probabilitat que l'interval
aleatori
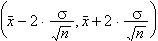 (##)
contingui el vertader valor de la mitjana µ és igual a 0,955,
en el sentit que si s'extraguessin un gran nombre de mostres de mida n
i es calculés formalment per cada mostra l'interval indicat, podem
esperar que un 95,5 % de vegades aquest interval contindria el vertader
valor de µ i, en canvi, el 4,5 % de vegades podem errar l'estimació.
Per aquest motiu, l'interval (##) rep el nom d'interval de confiança
amb un nivell de confiança del 95,5 % en l'estimació del valor
de µ. (##)
contingui el vertader valor de la mitjana µ és igual a 0,955,
en el sentit que si s'extraguessin un gran nombre de mostres de mida n
i es calculés formalment per cada mostra l'interval indicat, podem
esperar que un 95,5 % de vegades aquest interval contindria el vertader
valor de µ i, en canvi, el 4,5 % de vegades podem errar l'estimació.
Per aquest motiu, l'interval (##) rep el nom d'interval de confiança
amb un nivell de confiança del 95,5 % en l'estimació del valor
de µ.
- L'interval de confiança amb un nivell de confiança
del 95,5 % per a l'estimació de la mitjana µ d'una
variable estadística en una població, en la qual hem seleccionat
una mostra de mida (n
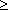 30), és l'interval 30), és l'interval 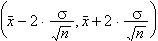 on on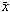 representa la mitjana mostral i s
la desviació estàndard de la variable en la població.
representa la mitjana mostral i s
la desviació estàndard de la variable en la població.
- Nota:
La idea de nivell de confiança és anàloga
a la de probabilitat d'encert. El seu contrari seria, doncs, risc
d'error (equivocació en l'estimació) i aquest és
el valor que en els con trastos d'hipòtesis rep el nom de nivell
de significació del test.
El radi de l'interval de confiança ens dóna el marge
d'error o variabilitat amb què cal expressar l'estimació.
Alerta, doncs, com ja hem comentat diverses vegades, a no confondre
el vocabulari.
- Nota: Tal com es va comentar en
l'apartat de l'estimació d'una proporció, si volem treballar
amb d'altres nivells de confiança, hem de canviar el 2 per d'altres
valors crítics corresponents a la distribució normal.
Així, per al nivell de confiança del 95 %, l'interval
de confiança de la mitjana està donat per una expressió
anàloga a (##) substituint-hi el 2 per 1,96. Si el nivell de
confiança fos del 90 % en lloc del 2 o de l'1,96, caldria posar
1,64.
En la fórmula que acabem de donar de l'interval de confiança,
podeu veure que es pressuposa que coneixem el valor de la desviació
estàndard de la població. Tal com hem dit a l'apartat anterior,
aquesta situació no serà la que es donarà habitualment
en treballs reals. Tanmateix, si les mostres són grans, la desviació
estàndard mostral corregida és un bon estimador de la desviació
estàndard d'una població i prendrà el seu paper en
l'expressió (##) de l'interval de confiança.
Per tant, en cas que vulguem estimar la mitjana µ d'una variable
estadística en una població sense conèixer el valor
exacte de la desviació estàndard s
d'aquesta variable en la població, seleccionarem una mostra aleatòria
de mida (n 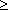 30)
i calcularem 30)
i calcularem 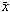 , la mitjana
mostral, i s, la desviació estàndard mostral, i llavors
podrem prendre l'interval , la mitjana
mostral, i s, la desviació estàndard mostral, i llavors
podrem prendre l'interval
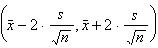 com una bona aproximació de l'interval de confiança
amb un nivell de confiança del 95,5 %.
com una bona aproximació de l'interval de confiança
amb un nivell de confiança del 95,5 %.
- Càlcul pràctic: en podeu veure exemples a la
pràctica 6, on veureu que l'Excel té molt
en compte la primera de les dues observacions que s'exposen seguidament.
Primera precisió: Amb rigor cal fer servir la t de Student.
Fins ara hem treballat amb mostres grans i així podem, per
una banda, aplicar el teorema del límit central, i per una altra,
substituir el valor de la desviació estàndard de la població
que apareix al teorema per la desviació estàndard corregida
mesurada sobre la mostra sense que això representi cap canvi substancial.
Tanmateix, en moltes circumstàncies no és possible treballar
amb mostres grans per fer l'estimació de la mitjana. Tot i que
no donarem la formulació teòrica d'aquests casos, sí
que comentarem, com ja es va fer per a l'estimació d'una proporció,
que el fet d'emprar la desviació estàndard corregida de
la mostra en lloc de la desviació estàndard de la població
(desconeguda en general en situacions pràctiques) ens porta a una
situació en què cal aplicar la distribució t de Student.
I llavors, quin valor caldria posar en lloc del 2 (que vol dir 2,00)
que assenyala el radi que dóna l'interval del 95,5 %? Semblantment,
si no volem treballar amb un nivell de confiança del
95,5 %, sinó amb un altre, quin nombre hem de posar?
La taula següent mostra alguns valors dels que
poden interessar. En trobareu més al llibre TAULES.XLS
que forma part dels materials del curs.
En aquesta taula, tn representa la distribució t de Student
amb 10, 15, 20... graus de llibertat corresponents a mostres de mida una
unitat més.
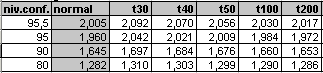
Tanmateix, veureu que no s'han inclòs mostres de
mides més petites que 30. En aquests casos, com que no es pot
aplicar el teorema del límit central, no es pot donar una fórmula
consistent per a l'interval de confiança de l'estimació
de la mitjana.
Segona precisió: Mostres sense reemplaçament.
Tot i que aquesta precisió és molt més habitual
en situacions d'estimació d'una proporció, també
en aquest cas cal comentar que si partim de la base que hem fet servir
mètodes de mostreig que no siguin exactament el MAS (mostreig
aleatori simple), sinó que s'hagin d'assimilar més aviat
a un mostreig sense reemplaçament, llavors cal una rectificació
de la fórmula que ens porta a multiplicar el radi de l'interval
de confiança pel factor 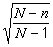 ,
en què N és la mida de la població on es
prenen mostres (que en aquest cas influeix) i n és la
mida de la mostra. ,
en què N és la mida de la població on es
prenen mostres (que en aquest cas influeix) i n és la
mida de la mostra.
És fàcil veure que la influència
d'aquest factor és inapreciable a efectes pràctics en
cas que el quocient n/N sigui més petit que 0,05. En aquestes
situacions, ja s'acostuma a considerar la població com a infinita
i llavors es pot aplicar la fórmula general, com si l'extracció
fos aleatòria simple. Això és el que fa sempre
l'Excel.
|
| |
|
 |
| |
Ampliacions, aclariments i comentaris |
| |
|
 |
Un exemple d'aplicació del teorema del
límit central a un cas discret
Si llancem 100 daus enlaire de manera independent, quina previsió
podem fer amb una probabilitat d'encert del 95,5 % pel que fa a la mitjana
de la suma dels punts? I pel que fa a la suma dels punts?
- En aquest cas, la població de partida (resultats possibles
de les tirades d'un dau) respon a una distribució uniforme discreta
amb valors extrems 1 i 6. La mitjana i la variància de la distribució
uniforme discreta amb valors {1..., n} són, respectivament,
(1 + n)/2 i (n2 – 1)/12. En aquest cas,
doncs, la mitjana és 3,5 i la variància 35/12. Podem calcular
la desviació estàndard i resulta 1,71.
- La mitjana mostral estarà, amb probabilitat del 95,5 %, en
l'interval centrat en el valor 3,5 i de radi 0,342, que és el
resultat de substituir
s = 1,71 i n = 100 en l'expressió
2 ·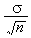
- L'interval és, doncs, (3,158; 3,842).
- Si sabem la mitjana d'un conjunt de 100 valors, podem conèixer
la suma simplement multiplicant per 100. Podem dir, doncs, que quan
tirem 100 daus enlaire i sumem el nombre de punts, l'interval en el
qual podem predir, amb una probabilitat d'encert del 95,5 %, que hi
haurà la suma de punts és l'interval (315,8; 384,2), però
com que la suma ha de ser un nombre enter, la resposta serà l'interval
[315, 385] i, per a aquest interval, la probabilitat serà una
mica superior a 95,5 %.
|
| |
|
 |
| |
|
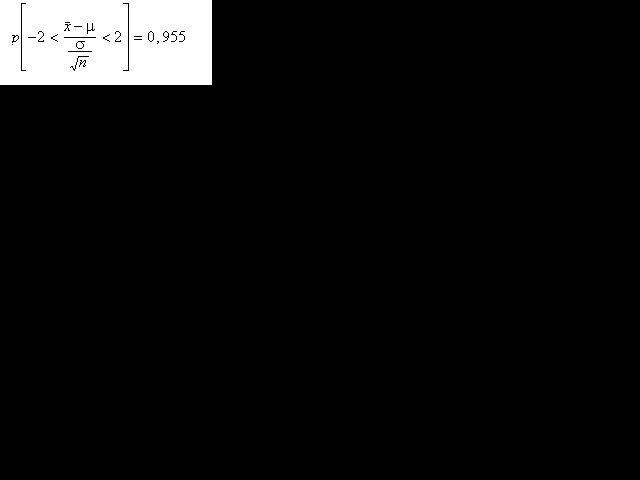
 (#)
(#)