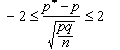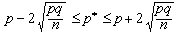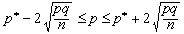|
|
Idees sobre estimació. Estimació d'una proporció 
Al mòdul 1 es comentava el marc general de treball de l'estadística
i es deia que l'ajustament d'unes dades a un model teòric per poder
inferir conclusions és una tasca habitual.
Hem vist al mòdul anterior uns exemples de contrastos d'hipòtesis,
amb la idea concreta de confrontar la validesa d'un model. En alguns d'aquests
casos, les característiques del model s'han deduït de les
pròpies dades: hem fet una inferència.
L'objectiu d'aquest document és presentar, des d'un punt de vista intuïtiu,
els aspectes més importants relacionats amb l'estimació de paràmetres
i estudiar més a fons l'estimació d'una proporció.
|
 |
El marc general de l'estimació |
|
|
Convé comentar, abans que res, la terminologia que s'empra.
 |
Paràmetre: és
una característica numèrica de la població. És
un nombre fix, però habitualment no en coneixem el valor. |
La determinació d'un paràmetre és una
de les fites que habitualment es marca el procés estadístic.
Tanmateix, la determinació exacta d'un paràmetre només
es pot fer a partir de l'anàlisi exhaustiva de tota la població,
moltes vegades fora de l'abast de l'investigador (per raons de temps,
de despeses...).
Llavors és quan la inferència es fa imprescindible: s'escull
una mostra que sigui representativa de la població i que
es pugui analitzar amb detall i a partir d'aquesta selecció i anàlisi
s'estima un valor per al paràmetre que interessa.
 |
Estadístic: és
una característica numèrica de la mostra. El valor d'un
estadístic es pot calcular després que haguem pres una
mostra i haguem mesurat sobre les seves unitats el valor de la variable
que ens interessa. |
 |
Estimador: és
qualsevol estadístic que calculem amb la finalitat d'estimar
el valor d'un paràmetre. |
Vegeu l'exemple següent:
Sigui el que sigui l'estadístic que es decideixi emprar, el seu valor
varia d'una mostra a una altra. Per a una decisió correcta sobre
la inferència d'un paràmetre de la població a partir
d'un estadístic, cal estudiar quina seria la variabilitat d'aquest
estadístic si es prenguessin moltes mostres: el que se'n diu la distribució
mostral de l'estadístic.
Per poder arribar a una estimació a partir de l'estadístic
escollit, ens caldria conèixer el model teòric que explica
la seva variabilitat, calculada suposant la població coneguda.
Això es pot fer amb raonaments teòrics (que escapen de la
finalitat d'aquest curs) o bé amb procediments empírics,
amb l'ajut d'un ordinador que ens permeti fer simulacions i prendre moltes
mostres.
En aquest cas, per fonamentar la inferència (pas de l'estadístic
mesurat sobre la mostra al paràmetre desconegut de la població),
abans es fa una simulació, a manera de treball de laboratori: es
parteix d'una població coneguda, es prenen moltes i moltes mostres
i s'observa com varia l'estadístic escollit. Així es pot
veure si servirà com a estimador i quin tipus de garanties tindrem
quan fem una estimació a partir d'una mostra.
- Exemple: Per valorar quin de tots els estadístics ja
inventats o els que es puguin inventar en el cas del bombo d'una rifa
és el millor, hauríem d'enfocar el cas des d'un punt de
vista invers. Prendríem un bombo amb 3.000 boles, per exemple,
i faríem moltes vegades l'experiència de treure una mostra
de 50 boles (si pot ser amb una simulació ràpida amb ordinador,
millor). Analitzaríem llavors quina és la distribució
estadística que ha resultat pel que fa als valors observats de
l'estimador, i si hi podem reconèixer un model teòric,
millor. Dels models observats per la variació de cadascun dels
estadístics considerats, decidiríem quin s'ajusta millor
al valor 3.000 del qual, amb aquest enfocament, hem partit. I una vegada
decidit el millor estimador, l'aplicaríem a la nostra mostra.
Aquesta opció empírica és la que adoptarem, amb
l'ajut de les simulacions que podem fer amb l'Excel, per a la presentació
dels dos problemes fonamentals d'estimació de paràmetres.
Podeu veure a la pràctica 1 un estudi del problema
del bombo que s'acaba de comentar. Convé que esmentem dos conceptes
importants que ajuden en la decisió de quin és el millor
estimador.
 |
Biaix d'un estimador:
es diu que un estimador no té biaix si la mitjana de la distribució
que dóna la variabilitat mostral coincideix amb el veritable
valor del paràmetre que volem estimar. Si, en canvi, la mitjana
dels valors que donaria l'estimador si realitzéssim totes les
mostres possibles s'allunya del veritable valor del paràmetre,
es diu que l'estimador és esbiaixat. |
- Podem esmentar, com a exemples fonamentals, que la mitjana d'una
mostra és un estimador sense biaix de la mitjana de la població,
i que, en canvi, la desviació estàndard (dita de vegades
no corregida, és a dir, calculada dividint per N)
d'una mostra és un estimador esbiaixat de la desviació
estàndard de la població (vegeu quin és el
millor estimador de 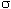 ). També
ens podem fixar en l'exemple del bombo: l'estimador màxim de
la mostra és esbiaixat. Si fem moltes mostres i calculem la mitjana
dels màxims nombres obtinguts en cada mostra, ben segur que obtenim
un valor menor que el nombre més gran que hi ha al bombo. ). També
ens podem fixar en l'exemple del bombo: l'estimador màxim de
la mostra és esbiaixat. Si fem moltes mostres i calculem la mitjana
dels màxims nombres obtinguts en cada mostra, ben segur que obtenim
un valor menor que el nombre més gran que hi ha al bombo.
 |
Precisió d'un estimador:
es diu que un estimador és més precís com més
petita sigui la variància de la distribució mostral
de l'estadístic que ha de servir per estimar el paràmetre
que interessa. Com a norma general, la precisió d'un mateix
estimador augmenta a mesura que augmenta la mida de la mostra considerada. |
Entre diversos estimadors, la consideració de l'existència
de biaix o no i la comparació de la precisió és el
que ens fa decidir per un o altre.
Els diagrames següents il·lustren la idea de biaix
i precisió aplicats a unes persones que es dediquen a llançar
dards cap a una diana.
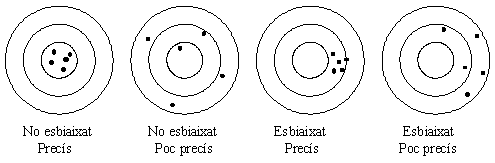
Quin d'aquests jugadors diríem que és un millor
llançador? Sense cap dubte, el primer. I el segon millor? Potser
ja dubtaríem entre el segon o el tercer. Ben segur que tots ens
posaríem d'acord que el pitjor és el quart.
Podem preguntar-nos quin hem de considerar que és el millor
estimador? Per donar una resposta intuïtiva a aquesta pregunta,
ens poden ajudar les simulacions i llavors entre dos estimadors que puguem
observar que no tenen biaix sempre escollirem el més precís.
Entre dos estimadors de la mateixa precisió sempre en triarem un
que no tingui biaix enfront d'un que en tingui. Algunes vegades, però,
s'opta per un estimador una mica esbiaixat, però molt precís
enfront d'un altre sense biaix però poc precís.
I, una vegada decidit quin és el millor estimador,
com anunciarem el resultat de la nostra estimació?
 |
Es diu que el valor de l'estadístic
dissenyat per a l'estimació d'un paràmetre dóna
una estimació puntual d'aquest paràmetre. |
Ara bé, la lectora o el lector, que ja estan a aquestes altures
força familiaritzats amb la tasca estadística, pensaran
que aquesta estimació ha d'anar acompanyada de la informació
del marge d'error (o grau de variabilitat) que pot tenir aquesta
estimació. I així és, en efecte.
 |
Error estàndard d'un estimador:
és la desviació estàndard de la distribució
que dóna la variabilitat mostral de l'estadístic corresponent.
Com més precís és un estimador, més petit
és el seu error estàndard. Qualsevol estimació
puntual d'un paràmetre ha d'anar sempre acompanyada de l'error
estàndard d'aquest estimador. |
- Exemples:
- L'error estàndard per a l'estimació de la mitjana
és l'error estàndard de l'estimació puntual
de la mitjana d'una població de la qual se suposa que la
variable que estudiem n'és una mostra seleccionada aleatòriament.
El valor que cal estimar per a la mitjana de la població
és el mateix que la mitjana de la mostra.
- El millor estimador de la desviació estàndard d'una
població és el valor que resulta de fer la desviació
estàndard corregida (dividint per N –
1), que és el nombre que ens dóna la funció
de l'Excel DESVEST (o la calculadora estadística amb la tecla
adient). Si es decidís emprar la desviació estàndard
no corregida, és a dir, dividint per N, s'obtindria
un estimador amb biaix. Vegeu la pràctica
5.
- La manera més usual de fer l'estimació d'un paràmetre
és la de donar un interval (dit interval de confiança)
al qual és plausible (amb el nivell de confiança
amb què es vulgui treballar) que pertanyi el veritable valor
del paràmetre que es vol estimar. Més endavant, es
defineix correctament aquest concepte.
Acabem aquest apartat introductori recordant el que dèiem al mòdul
anterior: l'estudi de la plausibilitat d'un model mitjançant un
contrast d'hipòtesis (per exemple, el test de khi quadrat) ja és
una forma d'inferència. Donem com a exemple el tipus de resposta
(sense parar atenció en els números) que caldria donar per
a cadascun dels tres models d'inferència que hem comentat per a
l'estimació del nombre de boles que hi ha al bombo:
En aquest mòdul treballarem a bastament els dos exemples principals
d'estimació que ens interessen, tot seguit l'estimació d'una
proporció i en un altre document l'estimació d'una mitjana.
|
 |
Estimació
d'una proporció |
|
|
Revisió del problema de la
predicció en el càlcul de probabilitats |
|
|
Per avançar en el camí que porta a l'estimació
d'una proporció, us recomanem que feu la pràctica
3 en el marc de la qual es defineixen intuïtivament i de manera
empírica, mitjançant simulacions, els conceptes següents, referits
a l'estimació d'una proporció:
Interval de confiança
Nivell de confiança
Tot seguit, revisarem un exemple que ja hem treballat anteriorment al
mòdul 4 per a mostres petites i, posteriorment, al mòdul 5 per a mostres
grans. Podeu veure la pràctica 2 del mòdul 4 on s'han
calculat probabilitats i valors crítics i la pràctica
3 del mòdul 5 on s'ha reprès l'exemple fent servir l'aproximació
de la distribució binomial mitjançant la normal.
Allà hem fet problemes de probabilitats a partir de models coneguts
i hem fet prediccions de possibles resultats, acompanyades de la probabilitat
d'encert que teníem amb aquestes prediccions. Ara reescriurem l'exemple
esmentat des d'un punt de vista més formal.
Exemple: En una població, el 47 % de les persones són
favorables a la gestió de l'ajuntament. Si s'encarrega una enquesta
que s'ha de fer a una mostra de 2.000 persones, quina és la predicció
que podem fer, amb una probabilitat d'encert del 95 %, respecte a la proporció
mostral?
- La distribució que representa la variable aleatòria
X (nombre de persones de la mostra favorables a la gestió
municipal) és una distribució binomial
B(n = 2000, p= 0,47) que pot ser aproximada per
una distribució normal amb mitjana
n · p = 940 i 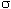 = =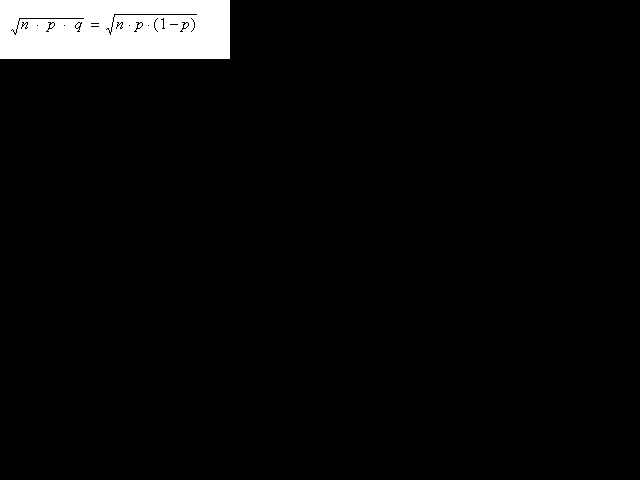 (aproximadament 22,32). (aproximadament 22,32).
- Aquesta consideració ja ha permès fer (vegeu mòdul
5) una previsió: "A la mostra sortiran entre 896 i 984
persones favorables", que té una probabilitat d'encert (nivell
de confiança) superior al 95 %.
- Però si el que ens interessa és estudiar la proporció
mostral, que és el tema que ara ens ocupa, podem veure que el
resultat anterior es pot enunciar dient, amb un nivell de confiança
del 95 %, que:
- La proporció mostral estarà entre 897/2000 = 0,4485
i 983/2000 = 0,4915.
- La proporció mostral estarà entre el 44,85 % i el
49,15 %.
- Podeu observar que això defineix un interval centrat en el
veritable valor de la proporció, que és 0,47 (o sigui,
el 47 %), i que d'aquest valor a cada extrem de l'interval hi ha una
distància (radi) de 0,0215. Podem formular, doncs, la conclusió
d'una tercera manera:
- La proporció mostral està a l'interval [0,47–r,
0,47+r] per un valor de r=0,0215.
- Aquest interval rep el nom d'interval de tolerància
(o, actualment, també interval de confiança) en
la predicció de la proporció mostral corresponent a un
nivell de confiança del 95 %.
- També podem enunciar amb percentatges quin és aquest
interval:
- Amb un nivell de confiança del 95 %, podem dir que la proporció
mostral pertanyerà a l'interval centrat en el 47 % que té
d'extrems 47 % - 2,15 % i 47 % + 2,15
%. Aquest interval s'enuncia sovint a la premsa com 47 % més
menys 2,15 %.
- El radi d'aquest interval rep moltes vegades la denominació
de marge d'error de la predicció i ens dóna una
mesura del grau de variabilitat amb què cal expressar l'estimació.
Si s'estudia formalment una situació anàloga
a la que es planteja a l'exemple, s'arriba al resultat que s'enuncia a
continuació. Podeu consultar la deducció i hi veureu per
què és habitual, actualment, prendre un nivell de confiança
del 95,5 %.
|
|
|
 |
L'interval de tolerància (també
anomenat interval de confiança) del 95,5 % de la proporció
mostral en la selecció d'una mostra aleatòria de mida
n a partir d'una població en la qual un determinat caràcter
es manifesta amb proporció p és l'interval [p–r,
p+r] centrat en el valor real de la proporció,
p, i de radi 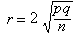 . . |
Exemple: En una empresa en què els estudis previs
demostren que el 4 % de la producció resulta defectuosa, se selecciona
una mostra de 1.000 unitats. Quina previsió podem fer d'unitats
defectuoses en la mostra seleccionada amb un nivell de confiança
del 95,5 %?
- El model seria la distribució binomial B(n=1000, p=0.04).
Com que n · p = 40 i també
n · q = 960 són més grans que 15, podem aplicar
sense cap dubte l'aproximació normal i és vàlid
el resultat anterior.
- L'interval de tolerància del 95,5 % estarà centrat,
doncs, en la proporció real p = 0,04 i tindrà
un radi igual (segons la fórmula donada) a 0,012.
- L'interval és [0,028; 0,052]
- La previsió que podem fer és que sortiran entre el 2,8
% i el 5,2 % de peces defectuoses (és a dir, en nombres absoluts,
entre 28 i 52 peces).
- I si féssim un control de qualitat i resultés que l'observació
no concorda amb aquesta previsió? Si ens ho mirem com un contrast
d'hipòtesi, tindríem criteris per rebutjar (amb un nivell
de significació del 4,5 %, que és el risc d'error de la
predicció) la hipòtesi que el 4 % de la producció
és defectuosa. Caldria revisar, llavors, les condicions de treball
de l'empresa.
|
|
|
El problema inferencial: estimació
d'una proporció |
|
|
Ja hem comentat diverses vegades
que la visió del procés d'estimació és l'invers:
no es parteix d'una població coneguda, sinó que, precisament,
es tracta d'estimar-ne un paràmetre a la vista d'una mostra. Ara
estudiarem aquesta situació, la pròpia dels problemes d'inferència que tractem
en aquest mòdul.
- L'estimació d'una proporció es fa per interval (l'anomenat
interval de confiança de l'estimació).
- L'interval de confiança es dóna centrat en la proporció
mostral p* observada i té per radi el mateix que tindria
l'interval de tolerància si la p* observada fos, realment,
la proporció mostral, p, de la població.
Exemple: En una població s'ha encarregat una enquesta a 2.000
persones per valorar la gestió municipal. En aquesta enquesta han
resultat 940 persones favorables a l'ajuntament. Quina estimació
podem fer pel que fa al percentatge de persones de la població favorables
a l'ajuntament?
- La proporció mostral observada és del 47 % (940 respecte
a 2.000). Hem vist abans, en la simulació ja comentada, que si
el veritable valor de la p de la població fos p
= 0,47, l'interval de tolerància del 95,5 % s'ha de donar amb
un marge d'error (radi de l'interval) del 2,15 %.
- L'estimació que farem serà la següent:
Amb un nivell de confiança del 95,5 % podem estimar
que la proporció de persones de la població favorables
a la gestió municipal està entre el 44,85 % i el 49,15
%.
- Quan els mitjans de comunicació publiquen resultats d'enquestes,
presenten habitualment les estimacions de proporcions com si fossin
estimacions puntuals. El resultat anterior seria publicat, segurament,
d'aquesta manera:
Titular: EL 47
% DE LA POBLACIÓ FAVORABLE A L'AJUNTAMENT!
A la lletra petita, inclòs en la fitxa tècnica
de l'enquesta (si hi és):
marge d'error: 2,15 %.
|
|


|
Per a una justificació del procediment que
acabem de comentar, que es concreta en l'enunciat que es dóna seguidament,
podeu consultar la part d'ampliació, on veureu les precisions que
cal fer, la principal de les quals és que es tracta d'una excel·lent
aproximació i no d'un resultat exacte.
- L'interval de confiança del 95,5
% en l'estimació de la proporció amb què es mostra
un determinat caràcter en una població, feta a partir
de la selecció d'una mostra aleatòria simple de mida n
és l'interval centrat en la proporció mostral observada,
p*, i de radi
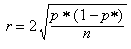 . .
- Habitualment, l'estimació es dóna en percentatge i
el radi de l'interval de confiança s'anomena marge d'error de
l'estimació.
Hi ha un altre aspecte que és important precisar pel que fa a
la validesa del resultat que acabem d'enunciar. S'ha indicat que la selecció
es feia amb una mostra aleatòria simple. Aquesta suposició
és equivalent a la de l'experiment de treure boles d'una bossa
a l'atzar i amb reemplaçament.
Tanmateix, a la pràctica, aquest no és el costum més
habitual, sinó que per raons de l'eficàcia del procés
de selecció es fan altres tipus de procediments de mostreig (mostres
sistemàtiques, mostres per conglomerats...) i llavors el procediment
cal modelitzar-lo més aviat mitjançant la distribució
hipergeomètrica, que regula les experiències d'extraccions
sense reemplaçament. Si es fa així, cal tenir en compte
la mida de la mostra, però, si la mostra és relativament
gran, les diferències no són substancials.
Podeu veure les fórmules si cliqueu a la icona
d'ampliació i podeu treballar el tema, a bastament, a la pràctica
4 d'aquest mòdul.
Exemple: En una enquesta feta a 1.200 persones, 333 s'han mostrat
partidàries d'una determinada opció. Quina estimació
podem fer amb un nivell de confiança del 95,5 %?
- Proporció mostral observada: 333/1200 = 0,2775 = p*
- Radi de l'interval de confiança:
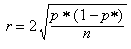
Posant-hi n = 1200 i p* = 0,2775, resulta 0,0259
- Estimació: la proporció és a l'interval [0,2516;
0,3034] o bé, en percentatges,
[25,16 %, 30,34 %]
- Una altra manera d'enunciar-la: proporció del 27,75 % amb un
marge d'error del 2,59 %.
Exemple revisat: En una enquesta feta a 1.200 persones, 333 s'han
mostrat partidàries d'una determinada opció. Quina estimació
podem fer amb un nivell de confiança del 95,5 % si la població on
s'ha fet l'enquesta té 10.000 habitants? I si té 30.000 habitants?
I si en té 80.000?
- Observem en primer lloc que 333 és el 27,75% de 1200.
- Si apliquem la fórmula corregida que podeu veure a l'ampliació
per k = 2 (valor corresponent al 95,5 %) en la població de 10.000
habitants el radi de l'interval de confiança resulta 0,0243,
o si ho volem expressar en tant per cent, el 2,43 %. Vist això,
l'estimació és que la proporció és a l'interval
[25,32 %, 30,18 %], és a dir, que és del 27,75 % amb un
marge d'error de 2,43 %.
- En la de 30.000 habitants, el resultat és que el marge d'error és
de 2,53 % per un interval de confiança de [25,22 %, 30,28 %].
- I si ho fem de manera semblant en el cas de la població de 80.000
habitants, resulta un marge d'error del 2,57 %.
- En tots tres casos, la diferència és ben petita, però
si enunciéssim el resultat de l'enquesta sense tenir en compte la correcció,
ens curaríem en salut, perquè diríem un marge d'error
més gran que el que tenim en realitat.
Hem vist com es dóna l'interval de confiança d'una estimació,
amb el seu valor central (proporció observada a la mostra) i el
radi de l'interval (també anomenat marge d'error). Tanmateix, escau
moltes vegades que un estudi estadístic (com és ara una
enquesta) no es limiti a l'estimació d'una única proporció.
Llavors, com que el radi de l'interval de confiança tal com l'hem
vist depèn del valor observat, cadascuna de les estimacions (enunciada
com a puntual per comoditat encara que això no sigui correcte conceptualment)
tindria un marge d'error diferent. Això faria que la publicació
de resultats fos molt enfarfegadora i també faria imprevisibles
a priori els marges d'error amb què es treballaria.
- Si s'estudien els valors de l'expressió
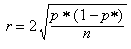 , es veu que assoleix el seu màxim
valor en el cas de màxima indeterminació, que correspon
a , es veu que assoleix el seu màxim
valor en el cas de màxima indeterminació, que correspon
a
p* = q* = 1/2. Aquest valor és 
- Per tant, el radi r de l'interval de confiança en l'estimació
d'una proporció (és a dir, el marge d'error) amb un nivell
de confiança del 95,5 % compleix, en tots els casos,
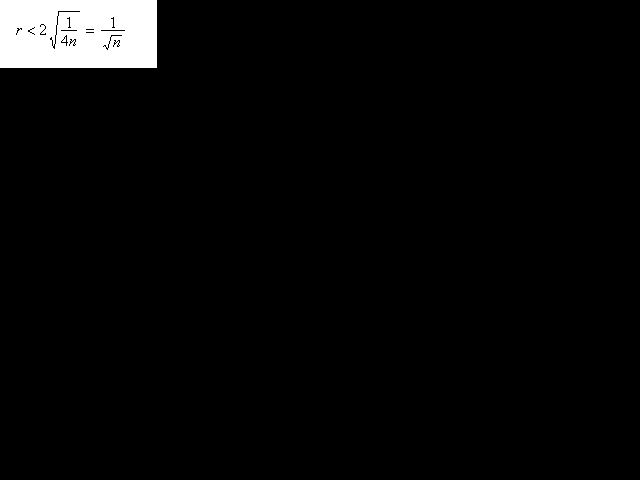
|
|
|
Observació:
No s'ha de confondre marge d'error de l'estimació, que és
el radi de l'interval de confiança, concepte lligat amb el tipus
de previsions que pot fer l'estadística, que no són mai exactes,
amb risc d'error, concepte contrari al de nivell de confiança
que resulta de la influència de l'atzar en les experiències
de mostratge que no ens permet mai fer cap previsió segura. Per evitar
l'ús de dues accepcions diferents del mot error, suggerim
les dues expressions que es donen tot seguit.
- marge de variabilitat: radi de l'interval
de confiança; aquesta expressió ens recorda com cal donar
les estimacions estadístiques.
- risc d'equivocació: expressió
que ens recorda que, tot i que tenim lleis que permeten treure conclusions
sobre l'atzar, aquest sempre ens pot fer errar en les nostres conclusions
encara que el procediment sigui correcte.
|
| |
|
|
|
Exemples:
- En el cas d'una enquesta feta a 1.200 persones, independentment del
valor (o valors) observats per a la proporció mostral, quin serà
el marge màxim d'error per a les previsions que puguem fer amb
un nivell de confiança del 95,5 %?
El màxim radi de l'interval de confiança és
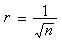 . .
Per n = 1200 resulta r = 0,0289; l'error màxim
és del 2,89 %.
- Si volem fer una enquesta amb diversos apartats, volem treballar amb
un nivell de confiança del 95,5 %, i volem que el marge màxim
d'error de les estimacions sigui del
3 %, quina ha de ser la mida de la mostra?
Si 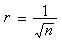 ha de ser 0,03, resulta
n = 1111 (aproximadament). ha de ser 0,03, resulta
n = 1111 (aproximadament).
Un darrer comentari molt important: us heu de fixar ben bé que en
tot el procés d'estimació la mida de la població
total no té cap influència teòrica en el procés.
La gràcia (i la immensa dificultat!) és escollir una mostra
que sigui realment representativa de la població. Si us fixeu en
fitxes tècniques dels mitjans de comunicació referides a poblacions
ben diferents, us podeu adonar d'aquest fet.
- La Vanguardia, maig de 1988. "Encuesta ante las presidenciales
norteamericanas. En la encuesta se consultó a 1.056 votantes
y existe un margen de error del 3 %."
- El País, setembre de 1989. "La mayoría
del electorado prevé otra victoria socialista. Muestra aleatoria
de 800 personas. Para un nivel de confianza del 95,5 % el error en la
hipòtesis más desfavorable seria del 3,5 % en más o en menos."
- El País, juny de 1989. "El 43 % de los barceloneses
cree que... El sondeo pulsó la opinión de 1.200 ciudadanos
y el margen de error és de más menos 2,9 %."
Ara bé, allò que estimem és
una proporció; en aquesta estimació, el marge d'error
és el mateix (en percentatge!) en els tres casos, però heu
de tenir ben present que un error relatiu del 3 % sobre la població
dels Estats Units o un error relatiu del 3 % sobre la població
de Barcelona donen errors absoluts ben diferents!
Podeu veure que els càlculs relatius a la mida de la mostra,
l'interval de confiança i el marge d'error en l'estimació
d'una proporció es fan ràpidament amb l'aplicació
d'una fórmula.
|
| |
| |
|
 |
| |
|
|
|
Ampliació 1: Deducció
de la fórmula de l'interval de tolerència
|
| |
Per enunciar-ho amb tot rigor, el que veurem
és la deducció de la fórmula que dóna l'interval de
tolerància (també dit actualment de confiança) en la previsió
del resultat de la proporció mostral en una simulació.
Si es pren una mostra aleatòria de mida n a partir d'una
població en què un determinat caràcter es manifesta
amb una proporció p, la distribució que representa
la variable aleatòria X (nombre d'elements de la mostra
que manifesten el caràcter estudiat) és una distribució
binomial B(n, p) que pot ser aproximada per la distribució
normal de mitjana n · p, i desviació estàndard
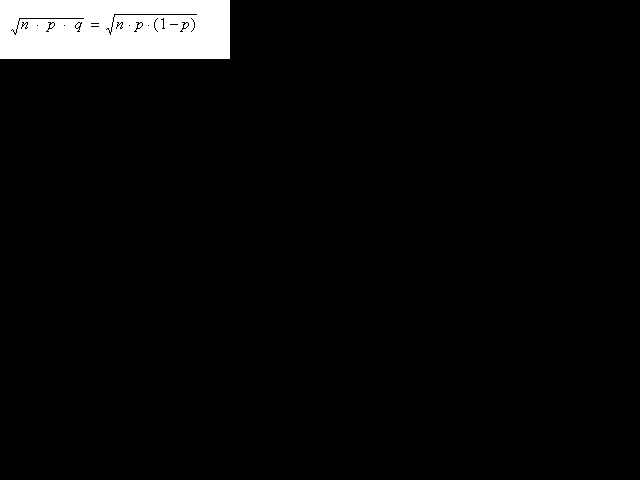 Això vol dir que la variable estandarditzada deduïda a partir
de X segueix una distribució normal estàndard, N(0,1).
Això vol dir que la variable estandarditzada deduïda a partir
de X segueix una distribució normal estàndard, N(0,1).
Ara bé, la proporció mostral és p* = X/n.
Si en la fórmula que ens dóna la variable estandarditzada
Z substituïm la mitjana i la desviació estàndard
pels seus valors i dividim numerador i denominador per n queda:
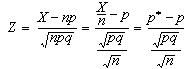
Com que Z és la distribució normal estàndard,
el que acabem de veure ens diu que la distribució de la proporció
mostral p* és una normal de mitjana p i desviació
estàndard
 Per altra banda, si consultem les probabilitats associades a la distribució
normal N(0,1) veurem quin és l'interval centrat en la mitjana que
defineix la probabilitat del 95,5 %:
Per altra banda, si consultem les probabilitats associades a la distribució
normal N(0,1) veurem quin és l'interval centrat en la mitjana que
defineix la probabilitat del 95,5 %:
p[– 2  Z Z  2] = 0.955 = 95,5% 2] = 0.955 = 95,5%
És a dir, que, en el nostre experiment, l'interval de tolerància
(o de confiança) del 95,5 %, això és, el conjunt
C de valors més plausibles de p* de manera que la
probabilitat p[ p* pertany a C] = 0.955 = 95,5 %, són els
que compleixen:
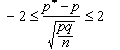
Equivalentment, si aïllem p*, trobarem aquesta expressió:
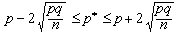
que ens permet enunciar la proposició inclosa al text.
Observació
Si en lloc de treballar amb un nivell de confiança del 95,5 % haguéssim
decidit fer-ho amb un altre, el número 2 seria substituït
pel corresponent valor de la distribució normal. Així, per
exemple, si volem intervals de tolerància per un nivell del
90 %, el valor seria 1,64, i si el nivell de confiança és
del 95 %, a la fórmula apareixeria 1,96.
|
| |
|
| |
|
 |
| |
|
|
|
Ampliació 2: Deducció
de la fórmula de l'interval de confiança
|
| |
Per deduir la fórmula que dóna
l'interval de confiança en l'estimació d'una proporció,
podem veure que si en la fórmula que dóna l'interval de tolerància
i que s'ha deduït anteriorment fem unes transformacions algebraiques
senzilles arribem a aquesta expressió:
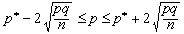
que és semblant però no del tot anàloga a l'anterior,
perquè p no està aïllat (apareix en tots els
termes).
Tanmateix, es demostra que si la mostra és prou gran, es pot
prendre com a negligible la diferència entre prendre el radi de
l'interval amb la veritable desviació estàndard de la distribució,
és a dir, 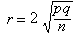 , o bé substituir-hi p
i q pels valors observats, , o bé substituir-hi p
i q pels valors observats,
p* i q* = 1 – p*, que serveixen com a
estimadors.
La diferència conceptual ve, llavors, del fet que si en el procés
d'estimació fem servir p* en lloc de la p desconeguda,
la proporció mostral no segueix una distribució binomial
(que si n és prou gran, es pot aproximar per una normal),
sinó una distribució anomenada t de Student amb n – 1
graus de llibertat, en què n és la mida de la mostra.
I llavors, quin valor caldria posar en lloc del 2 (que vol dir 2,00) que
assenyala el radi que dóna l'interval del 95,5 %?
La taula següent, on t10, t30..., t1600 representen
les distribucions t de Student amb 10, 30... 1600 graus de llibertat,
ho mostra:

Vegeu que per les mides de les mostres aconsellables en una enquesta
adreçada a estimar una proporció la diferència és
ben minsa.
Podem prendre, doncs, com una excel·lent aproximació del
radi de l'interval de confiança (si el nivell de confiança
és del 95,5 % i la mida de la mostra és la usual en enquestes)
el valor de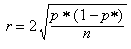
Així, s'arriba a l'enunciat sobre l'interval de
confiança d'una estimació que s'ha donat al text.
|
| |
|
 |
| |
|
|
|
Ampliació 3: Fórmules
aplicables si es consideren mostres sense reemplaçament
|
| |
Si es considera l'experiència de treure boles d'una bossa amb reemplaçament
i amb independència d'una extracció a l'altra, el model
teòric és la distribució binomial i en cada extracció
la probabilitat d'èxit és la mateixa.
En canvi, si traiem boles sense reemplaçament, les extraccions
no són independents i la probabilitat d'èxit va variant.
Així, per exemple, si a la bossa hi ha N boles (mida de
la població) i en la primera extracció la probabilitat de
treure bola blanca és b/N, si la primera bola és
blanca a la segona extracció la probabilitat serà (b-1)/(N-1),
però si la primera no ha estat blanca la probabilitat que ho sigui
la segona és b/(N-1), etc. Si el valor de N
és molt gran, sovint les diferències són inapreciables,
però si no ho és tant, llavors cal tenir-ho en compte.
Per això, si es fa una enquesta sense reemplaçament, en
aquest cas s'ha de considerar un factor de correcció en el radi
de l'interval de confiança de l'estimació d'una proporció.
En aquest factor intervé la mida de la població i les fórmules
que s'han de considerar són les següents:
- Interval de confiança per a l'estimació d'una proporció
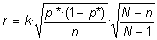
- Error màxim d'estimació
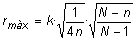
En aquestes fórmules k representa el valor crític segons
el nivell de confiança i la distribució amb què vulguem
treballar. Habitualment, és k = 2 si considerem el nivell
de confiança del 95,5 % i l'aproximació donada per la distribució
normal. Altrament, podeu consultar la taula corresponent
una mica més amunt.
Adoneu-vos d'alguns valors d'aquest factor de correcció:
- En una població de mida 100.000, si es fa una enquesta amb
mida de la mostra igual a 1.000, el valor d'aquest factor és
0,995. Per aquesta raó, s'acostuma a considerar en aquest cas
que la població és infinita.
- En una població de 1.000 persones, amb una enquesta feta a
200 persones, el factor indicat té un valor de 0,895.
- I, en tot cas, el factor de correcció fa que els intervals
resultants siguin més petits que si no el considerem. Per aquesta
raó, si en lloc d'aplicar aquestes fórmules corregides
donem el valor resultant de les fórmules sense corregir, en realitat
el nivell de confiança és més gran que el que en
realitat anunciem.
|
| |
|
 |
| |
|
| |
|

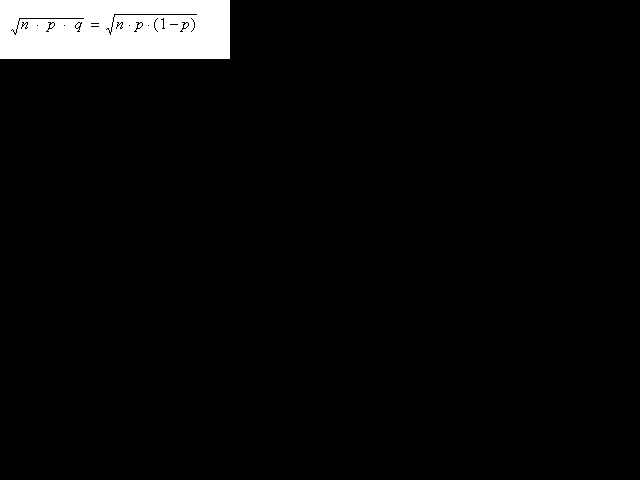
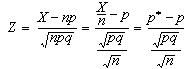

 Z
Z  2] = 0.955 = 95,5%
2] = 0.955 = 95,5%