Al mòdul 2, mentre es presentaven els conceptes de l'estadística descriptiva, es va fer una referència a les dues tecles de desviació estàndard que es troben a les calculadores estadístiques.

S'ha dit que la desviació calculada amb denominador n és qualificada pels manuals com a desviació tipus poblacional o bé com a desviació estàndard no corregida, i la segona, la que es calcula amb denominador n _– 1, s'anomena desviació tipus mostral o, de vegades, desviació estàndard corregida.

El fet que alguns models de calculadora "no encertin" del tot aquestes denominacions (i una errada als apunts, que ara ja s'ha corregit) va obrir durant el curs 2002-2003 un debat en el fòrum del D28 que va acabar amb un aclariment del professor Carles Barceló (autor dels materials del curs de l'any 1988 gènesi de l'actual D128) que tot seguit transcrivim:

Sobre com s'ha de denominar una desviació estàndard i l'altra és un tema polèmic. Si calcules la desviació estàndard amb denominador N, estàs indicant indirectament que el teu objectiu no és estimar la desviació estàndard d'una població desconeguda de la qual les dades en són una mostra, ja que si fos aquesta la teva intenció, utilitzaries la desviació estàndard amb denominador N-1.
Per tant, calculant la desviació estàndard amb denominador N, estàs indicant que el teu interès és calcular la desviació d'aquelles N dades i prou, amb caràcter descriptiu, sense cap pretensió de fer cap tipus d'estimació. Això equivaldria a dir que la teva "població" són aquelles N dades i, per tant, justificaria que s'anomeni desviació estàndard poblacional.
En canvi, quan estàs calculant la desviació estàndard amb denominador N-1, dius implícitament que aquelles N dades són una mostra d'una població més gran i que el que pretens és estimar la desviació estàndard desconeguda d'aquesta població a partir del coneixement de la desviació estandard -amb denominador N-1- de la mostra. Per aquest motiu, no sembla estrany anomenar-la desviació estàndard mostral. En qualsevol cas, jo em guardaria molt d'anomenar-la mai desviació poblacional (tot i que ho han fet alguns manual de calculadora), ja que no ho és: només és un estimador de la desviació estàndard de la població.

Una cosa més: jo sempre m'estimo més que la gent treballi amb variàncies i no amb desviacions estàndard, ja que mentre la variància amb denominador N-1 és un estimador centrat de la variància poblacional desconeguda, la desviació estàndard amb denominador N-1 no és un estimador centrat de la desviació estàndard poblacional desconeguda, cosa que, d'entrada, sobta a molta gent... i en canvi, és el reflex d'una senzilla propietat algebraica.

Aquesta reflexió encamina molt bé el tema que es vol tractar en aquesta pràctica, que és el de constatar empíricament per què interessa fer servir la DESVEST (dividint per N - 1) en els processos d'estimació i no DESVESTP (dividint per N).

I, encara més vista l'observació que acabem de llegir, per fer les estimacions treballarem amb variàncies que anomenarem tota l'estona com fa l'Excel: VAR (variància corregida o variància mostral, dividint per N - 1) i VARP (dividint per N).

A fi i efecte de visualitzar el que s'ha comentat a la introducció, convé treballar amb mostres petites. Efectivament, si n és de l'ordre de 100, el factor que passa de la DESVESTP a la DESVEST (que, escrit com faríem a l'Excel és =RAÍZ(100/99)) és de l'ordre d'1,005, que és inapreciable a efectes pràctics elementals. Com a les variàncies, amb una mostra de mida 100 hem de multiplicar per 100/99 = 1,010 per passar de VARP a VAR.

Per aquesta raó, començarem la pràctica prenent mostres de mida 20 a partir d'una població que se suposa que segueix el model normal. Sovint es comença a parlar de mostres grans si la mida de la mostra supera 30.

Simularem la presa de 200 mostres i analitzarem què passaria si volguéssim prendre la VARP dels valors observats en la mostra com a estimador de la variància de la població.

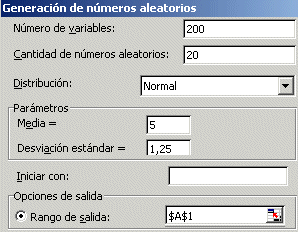
• En un full nou de càlcul, accediu a Herramientas | Análisis de datos | Generación de Números aleatorios i, de manera del tot anàloga al que ja heu anat fent en pràctiques anteriors, genereu 200 mostres de mida 20 a partir d'una població normal de mitjana 5 i desviació estàndard 1,25. Com que fareu algunes repeticions de les proves, no cal que poseu res a Iniciar con.

• A la cel·la A21 podeu posar un títol que indiqui que a la fila següent tindreu la VARP de cadascuna de les mostres.
• A la cel·la A22 escriviu la fórmula =VARP(A1:A20).
• Copieu la fórmula anterior a totes les cel·les que interessen d'aquesta mateixa fila, a saber, el rang B22:GR22.

Ja teniu una simulació que us permet copsar com seria la distribució de l'estadístic VARP mostral. Si voleu anar fent proves, només cal que torneu a activar ...| Generación de números aleatorios i accepteu sense fer cap canvi.

Aquest és un estadístic esbiaixat cap a l'esquerra. Hi ha diverses maneres d'observar-ho intuïtivament. Vegem la primera:

• La primera idea seria mirar el percentatge de vegades que aquest estimador ha quedat a l'esquerra del vertader valor de la variància en la població, que és 1,25² = 1,5625. Si s'allunya força del 50 %, això serà un primer criteri intuïtiu per convèncer-nos del biaix. Poseu a la cel·la A23 un títol, si voleu. A la cel·la B23 podeu posar la fórmula que ens dóna el nombre de vegades que s'ha produït el que dèiem, que és: =CONTAR.SI(A22:GR22; "<=1,5625") on convé que observeu el rang i la forma com escrivim la condició que volem comprovar. Si voleu el tant per cent al costat del nombre anterior, podeu escriure a la cel·la C23 la fórmula =B23/200 i amb Fomato | Celdas | Número escollir l'opció Porcentaje amb dues xifres decimals.

Ben segur que si aneu fent diverses proves de la generació de mostres i observeu els tants per cent que apareixen a C23, tindreu una idea clara del biaix cap a l'esquerra de l'estimador VARP, la variància calculada dividint per n.

• Seria millor fer un histograma que posi de manifest globalment i visual el que acabem de dir.
  
  • Veureu de seguida que les dades que voleu representar tenen una gran variabilitat. Us suggerim de fer servir com a delimitadors de les classes els nombres de 0,6 a 2,8 amb intervals de 0,2.
  • Llavors, heu de fer, en primer lloc, Herramientas | Análisis de datos | Histograma per fer la taula de valors del rang $A$22:$G$R22 i el rang de classes on hagueu anotat els nombres anteriors.
  • Després, fareu el gràfic (Gráfico de columnas) i l'arreglareu convenientment (perquè sigui un histograma, recordeu sobretot Formato de serie de datos | Opciones | Ancho del rango = 0).
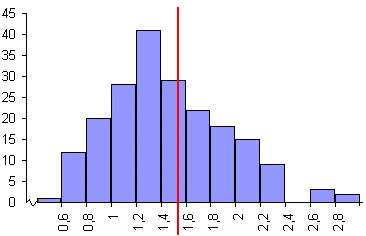
  • Vegeu el gràfic resultant per les dades que provenen de la simulació fet amb Iniciar con 3,1416. Com en una pràctica anterior, hem fet una petita modificació del gràfic a mà per indicar el vertader valor del paràmetre que volem estimar. En aquest cas, el 62 % dels valors observats han quedat a l'esquerra del valor real.

  
  

  
  
• Ara bé, el biaix d'un estimador no fa referència al percentatge que acabem de comentar, sinó a la mitjana de la distribució mostral de l'estimador, cosa que no sempre coincideix si aquesta distribució mostral no és simètrica. I aquest és el cas: de fet, el perfil que observeu és el d'una distribució . Per tant, cal fer els càlculs de la mitjana de la distribució mostral de l'estimador VARP (en realitat, no calculareu el seu valor teòric, sinó el que observeu en la simulació). Escriviu a E23 un rètol, Mitjana de VARP observats, i llavors a F23 la fórmula =PROMEDIO(A22:GR22) Encara es fa més clar, però ara amb consistència teòrica, el que es veu al gràfic: es tracta d'un estimador esbiaixat cap a l'esquerra. Per exemple, en el cas ja comentat (el que correspon a l'histograma), el valor que surt és 1,4656 (enfront de 1,5625 del valor real de la variància de la població). Si feu altres proves de simulacions (ja hem explicat com), veureu que pràcticament sempre la mitjana de la distribució mostral de l'estimador (la que marca si l'estimador té biaix o no) dóna un valor més petit que 1,5625.

• I per als afeccionats i afeccionades, es pot consultar la deducció teòrica que mostra per què es defineix la variància corregida dividint per n - 1 en lloc de dividir per n.

Podríeu substituir a la fila 22 la fórmula VARP per VAR i tot s'actualitzaria, però potser és més interessant poder comparar l'un i l'altre estimador.

• Escriviu, per exemple, a la cel·la A25 un títol que indiqui que a la fila següent tindreu la distribució mostral empírica de les VAR observades.
• A la cel·la A26 escriviu la fórmula =VAR(A1:A20).
• Copieu la fórmula anterior a totes les cel·les que interessen d'aquesta mateixa fila, a saber, el rang B26:GR26.
• Si voleu, per curiositat podeu comptar el percentatge d'observacions que queden a l'esquerra del vertader valor de la variància. Poseu a la cel·la A27 un títol; a B27 poseu la fórmula =CONTAR.SI(A26:GR26; "<=1,5625") i a la cel·la C27 (a la qual donareu el format de tant per cent) la fórmula =B28/200.

Veureu que, moltes vegades, més del 50 % de les observacions queden a l'esquerra del valor real. I ara ens preguntem: "Però no s'ha dit que VAR ha de ser un estimador sense biaix?". Efectivament, però és que el biaix fa referència a la mitjana de l'estimador. I com que el perfil de l'histograma seria essencialment el mateix que ja hem vist (de fet, els valors són els mateixos que abans multiplicats per un nombre fix), és a dir, una distribució , que no és gens simètrica, sinó que té una cua cap a la dreta, doncs és natural que més del 50 % de dades quedin a l'esquerra de la mitjana.

• Escriviu a E27 un rètol, Mitjana de VAR observats, i llavors a F27 la fórmula =PROMEDIO(A26:GR26), i si aneu fent proves de simulacions (recordeu que només heu de tornar a començar el càlcul de nombres aleatoris), veureu que realment es tracta d'un estimador ben centrat respecte al vertader valor d'1,5625.
• Per tenir una idea del valor de l'error estàndard d'aquest estimador, podeu posar a H27 el títol Err. est. aprox. i a I27 la fórmula corresponent, =DESVEST(A26:GR26)/RAIZ(20).
  

És clar que aquestes constatacions empíriques que acabem de fer haurien d'anar acompanyades de les corresponents deduccions teòriques, que en aquest cas es basen en el fet que la distribució mostral de l'estadístic VAR de la mostra segueix, tret d'un factor de proporcionalitat, el model d'una distribució , i permeten establir el valor efectiu de l'error estàndard d'estimació (si volem l'estimació puntual) o bé la fórmula de l'interval de confiança per a l'estimació de la variància de la població.

Repassem, doncs, les conclusions:

• VARP és un estimador esbiaixat cap a l'esquerra.
• VAR és un estimador centrat.
• DESVESTP és un estimador esbiaixat cap a l'esquerra.
• DESVEST és un estimador esbiaixat a l'esquerra però no tant com l'anterior.

Per tant, per estimar la desviació estàndard d'una població, n'estimarem la variància amb VAR, i llavors calcularem la desviació estàndard estimada. I això no és el mateix que calcular directament la DESVEST i fer-la servir com a estimador?

• A la pràctica, i només com a estimador puntual, sí!
• Conceptualment ja hem vist que no.
• Si es vol estudiar l'interval de confiança de l'estimació, llavors és imprescindible fer-ho amb la variància, perquè coneixem el model teòric de la distribució mostral de l'estimador: una distribució khi quadrat.
• I a partir de l'interval de confiança de la variància, es pot deduir l'interval de confiança en l'estimació de la desviació estàndard (que no serà centrat en el valor estimat).

Proposta d'ampliació

Podeu constatar que totes les conclusions segueixen essent vàlides encara que la població de partida no sigui normal.

Podeu provar-ho amb mostres generades aleatòriament a partir d'una població uniforme en l'interval [a, b] que té mitjana (a + b)/2 i variància (b - a)²/12. Per exemple, podeu fer servir, com a la pràctica anterior, la distribució uniforme en l'interval [0, 10].

Realment, aquesta afirmació sobta a primera vista. Si la variància és el quadrat de la desviació estàndard, com pot ser que si l'estimador VAR és centrat, en canvi, DESVEST tingui biaix com a estimador?

Perquè el concepte de biaix d'un estimador no fa referència a una estimació única, sinó a la mitjana de la distribució mostral d'aquest estadístic. I el fet que la mitjana de la distribució mostral de l'estadístic VAR ens doni el vertader valor de la variància s² de la població, no vol dir, ans al contrari, que la mitjana de la distribució mostral de l'estadístic DESVEST doni s i això és, justament, perquè cada valor puntual de VAR és el quadrat de cada un de DESVEST.

La propietat algebraica en què es basaria la demostració d'aquest fet és una generalització de la que podeu veure seguidament:

Suposem que sabem que 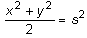(noteu la similitud amb què la mitjana de dues variàncies observades sigui una altra variància). Si ens adonem que 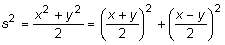concloem de seguida que 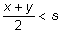(i ara, continuant la similitud, adoneu-vos que això vindria a dir que la mitjana de les dues desviacions estàndard és més petita que la desviació estàndard global).

La mitjana de l'estadístic VARP és igual a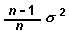

Si designem la mitjana com és habitual, VARP = S², la mitjana i variància de la població com m i s² i E [..] representa l'esperança matemàtica o mitjana d'una variable, tindrem

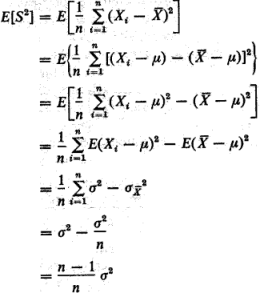
Això demostra que VARP no és un estimador centrat de la variància de la població, perquè la mitjana de la distribució mostral de l'estimador no coincideix amb el vertader valor.

En canvi, amb un senzill càlcul, es veu llavors que VAR = 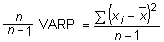, és a dir, la variància corregida sí que és un estimador centrat.