|
||||||||||||||||
| Pràctica |
Exercicis
|
|||||||||||||||
|
Glossari
|
||||||||||||||||
| Les distribucions de probabilitat contínues
|
|||||
| En aquest document es donen elements per a l'estudi de les distribucions de probabilitat contínues i se n'analitzen els models fonamentals, amb la distribució normal al capdavant, la qual, a més de la seva importància intrínseca, ens serveix per calcular els valors de la distribució binomial quan l'ordinador «falla» (és a dir, que no pot obtenir-los perquè <I>n</I> té un valor massa gran.) | |||||
|
|
Idees prèvies | ||||
|
L'estudi de les variables aleatòries ha d'anar acompanyat de la consideració del càlcul de les probabilitats dels esdeveniments que interessa considerar. En el cas de les variables discretes, l'element fonamental de l'estudi són les probabilitats d'uns certs valors (que formen un conjunt de nombres aïllats), els únics valors que es poden observar com a resultat de l'experiment. Per construir el model de probabilitat que permeti fer amb més rigor la tasca d'inferència en experiències que tinguin associada una variable numèrica contínua, heu de tenir en compte diverses idees que es comenten tot seguit. La idea de continuïtat, diuen els teòrics, és una noció intuïtiva. Fins i tot s'escriu, de vegades, que els nombres reals només són la formalització d'aquesta idea. En les situacion s d'aplicació real, ens trobem que hem de fer servir la continuïtat quan volem mesurar algunes magnituds (temps, longitud...). Ja hem comentat al mòdul d'estadística descriptiva que:
Per treballar amb una variable numèrica contínua hem de reflexionar al voltant del concepte de precisió en el procés de mesura. En aquests tipus de variables, no tenen sentit les expressions del tipus X=a, sinó que sempre s'ha de pensar en valors localitzats en un interval. Per exemple, si diem que una persona pesaLes consideracions associades amb la mesura tenen una influència molt important quan es vol modelitzar una distribució de dades d'una variable contínua. Es pot dir que la necessitat de mesurar i donar forçosament la mesura arrodonida d'acord amb l'instrument de mesura (o amb les circumstàncies de l'estudi que fem) fa que el concepte intuïtiu de continuïtat (i les distribucions de probabilitat contínues) esdevingui teòric i només s'hi pugui arribar com a límit de les distribucions discretes, que són aquelles amb què realment treballem a la pràctica. En els documents de fonaments del mòdul 4, La
probabilitat i Les
distribucions de probabilitat discretes, quan s'establia la diferència
conceptual entre les distribucions de probabilitat discretes i les contínues,
ja es comentava que per a una variable aleatòria contínua
no hem de tendir a buscar la probabilitat d'assolir un valor fix, perquè
si anomenem X la variable numèrica contínua que estudiem
i a és un nombre real, llavors l'esdeveniment X=a
no és un observable per a l'experiment. Per això
podem prendre gairebé com una definició:
La idea que per una variable contínua només podem treballar amb valors arrodonits de la variable fa que, en general, només es puguin estudiar esdeveniments que es puguin representar pel fet que el valor de la variable pertanyi a un determinat interval (o agrupació d'intervals). Els elements fonamentals de treball seran, doncs, les probabilitats de la forma
De la mateixa manera que a l'hora de cercar quin model teòric correspon a una distribució estadística discreta es confronta el diagrama de barres estadístic amb el diagrama de barres de la distribució de probabilitat que creiem que ha de ser el model segons les circumstàncies de l'experiment, l'intent d'idealitzar el perfil dels histogrames per a les variables contínues ens porta a buscar l'essència de la distribució fent els intervals de classe cada vegada més petits. En els histogrames el que ens fa veure la freqüència (relativa) de dades en cada interval de classe és l'àrea de cada rectangle. A partir d'aquí, quan passem de dades empíriques al model teòric hom imagina una funció contínua amb la propietat que les àrees sota aquesta corba contínua siguin les que serveixin per determinar els valors de les probabilitats. Així, arribem a l'element de treball fonamental amb les distribucions contínues.
|
|||||
|
|
La distribució uniforme contínua | ||||
|
Presentarem, primer de tot, un exemple que ens pot ajudar a entendre els conceptes que seguiran. Com en el cas discret, comencem per la distribució uniforme contínua.
Es tracta del model teòric associat amb experiments en què els valors que pot prendre la variable són tots els d'un interval de la recta real, [a, b], de manera que la probabilitat es reparteix uniformement al llarg de tot l'interval. De seguida se'ns acut que la funció que permet calcular la probabilitat ha de tenir un aspecte semblant al d'aquest gràfic:
I si ha de ser l'àrea sota la corba la que serveixi per calcular la probabilitat, l'àrea tramada ha de ser igual a la unitat (tota la probabilitat). Un exemple que habitualment donen els tractats d'estadística per a la funció uniforme (i que a casa nostra sovint ens sembla que prové del món de les idees) és el que parla d'una línia d'autobusos que passen exactament cada 10 minuts. Una persona, en acabar el treball, va a buscar aquest autobús. Les circumstàncies de la feina fan que es pugui pensar que arriba a la parada en un moment aleatori. El model de probabilitat que regula l'estona que ha d'esperar l'autobús és la distribució uniforme. Si us pregunten quina és la probabilitat que aquesta persona s'hagi
d'esperar entre 3 i 5 minuts, és pràcticament segur que
donareu una resposta intuïtiva: 2/10. Dels 10 minuts de l'interval
de màxima espera possible ara se'ns pregunta per un interval de
2 minuts. Com que tots els instants són igualment probables, 2
minuts entre 10 representen una probabilitat igual a 2/10.
L'àrea és 2 · 1/10 = 2/10. Aquest valor confirma la intuïció: així es calcula la probabilitat. I si ara ens preguntem per la probabilitat d'esperar-se entre 3 minuts
i 3 minuts i mig? Si fem el dibuix i calculem l'àrea (o fem funcionar
la intuïció), contestarem que la probabilitat ha de ser 0,5
· 1/10 = 0,05.
Figura 3 El rectangle que serveix per calcular la probabilitat ja ha esdevingut, quasi, una línia. I si, finalment, ens preguntem per la probabilitat d'haver-se d'esperar
exactament 3 minuts? Ara sí que el rectangle ja és un segment.
I un segment no té àrea. Però... observeu que de la mateixa manera que ajuntant molts i molts segments (una infinitat) es pot arribar a tenir un rectangle (per això de vegades es diu que l'àrea d'un segment o rectangle infinitament petit no és pas 0, sinó que té un diferencial d'àrea), també hem de constatar que com a reunió de molts i molts esdeveniments de probabilitat 0 (una infinitat de no observables, que podríem dir que tenen cadascun d'ells un diferencial de probabilitat) s'aconsegueix un esdeveniment observable. L'exercici 6 us permetrà treballar amb una variant d'aquesta situació i confrontar-la amb el model normal que s'exposa més avall. |
|||||
|
|
La funció de densitat de probabilitat | ||||
|
L'exemple anterior mostra que, si bé en el cas discret es pot parlar de funció de masses per indicar la funció de probabilitat perquè la unitat, com a probabilitat total (o massa) queda repartida entre una col·lecció de punts aïllats, per a les distribucions contínues no hi ha punts pesants, sinó que la probabilitat es reparteix en tota la recta, o en un interval, i es parla de densitat de probabilitat per explicar com es fa aquest repartiment entre totes les zones que considerem probables... com el que es fa en alguns problemes de mecànica per explicar com es reparteix la massa d'un objecte.
És important comentar el fet que els valors de la densitat de probabilitat no donen, directament, el valor de la probabilitat, sinó que aquesta funció és un element teòric que permet establir la probabilitat d'un interval en una distribució contínua. Podem fer servir la notació d'integral i donar la definició següent:
Nota: Tot i que d'altres definicions que donarem més avall també s'expressen de manera més "elegant" amb la notació integral, convé indicar, però, que no fa cap falta saber integrals per seguir el curs; cal posar l'èmfasi en el punt de vista intuïtiu que acompanya totes les definicions. |
|||||
|
|
La funció de distribució de probabilitat | ||||
|
De manera semblant al que s'ha fet en el cas discret, per a les variables contínues es defineix un element de treball fonamental que dóna la probabilitat acumulada.
A diferència del que passa amb la funció de probabilitat de les distribucions discretes i la funció de densitat de probabilitat de les distribucions contínues, que són elements de treball essencialment diferents, la funció de distribució té característiques semblants en un cas i en l'altre. En aquest sentit, interessa comentar que la probabilitat
que el valor observat de la variable pertanyi a un interval (i
ja s'ha dit que aquest tipus de probabilitats són els elements
fonamentals de treball amb les distribucions contínues) es pot
expressar a partir de la funció de distribució: Així ho farem en les pràctiques amb el programa Excel (i també es faria en el treball manual amb taules estadístiques). Notes:
Tal com passava en el cas discret, la funció de distribució de probabilitat acumulada té les propietats següents:
Però ara es verifica que:
|
|||||
|
|
Paràmetres d'una distribució de probabilitat contínua | ||||
|
Hem introduït els paràmetres de les distribucions discretes per analogia amb els conceptes estudiats per a les distribucions estadístiques. Anàlogament, per a les distribucions de probabilitat contínues, es defineixen:
Si us interessa, podeu consultar la definició formal d'aquests paràmetres. En els apartats següents es presenten des del punt de vista conceptual dues d'aquestes distribucions (la normal i l'exponencial) i en altres moments del curs, quan escaigui, se'n presentaran d'altres. Alhora us fem saber que en aquest mòdul es mostra la resolució de problemes de probabilitats relacionats amb les distribucions contínues emprant l'Excel.
|
|||||
|
|
La distribució normal | ||||
| Moltes situacions experimentals per
a les quals els valors observats poden ser, teòricament, nombres
qualssevol d'un interval en la recta real poden ser estudiades amb el model
conegut amb el nom de distribució normal, que és el que idealitza
els histogrames en forma de campana amb què us heu trobat sovint:
en mesures antropomètriques, en mesures experimentals al laboratori,
en distribucions que recullen rendiments en alguna prova o test, etc. Quines
són les característiques que té aquest model?
Podem pensar que una distribució estadística que recull els valors d'una variable contínua correspon al model normal si la idealització del seu histograma (perfil) ens mostra una corba simètrica, amb un únic màxim, que coincideix amb la mitjana. Si la corba normal ha d'ajustar una distribució de dades començarem per l'observació del perfil de l'histograma i recordeu que ja tenim un criteri intuïtiu (coincidència de la mitjana i la mediana) i un altre de numèric (el coeficient d'asimetria, que ha de ser aproximadament 0) per a valorar la simetria d'una distribució de dades empíriques. La forma de la corba normal es caracteritza també per l'existència de dues llargues cues, i per un cert grau d'apuntament que podem valorar amb el coeficient de curtosi.
Per representar la distribució normal de mitjana m
i desviació estàndard
Els percentatges de dades que, per a la distribució normal, pertanyen als intervals
són ben coneguts i característics d'aquest model, amb aquests valors aproximats:
Per intuir si el nostre conjunt de dades empíriques té un bon ajustament amb el model normal o no, a més de les altres característiques ja comentades, compararem els percentatges de la distribució estadística amb els que acabem de donar.
Observeu que apareix l'expressió d'estandardització de la variable X, cosa que amb la distribució normal té una importància especial.
Els valors de les probabilitats de la distribució normal estàndard estan tabulats en la majoria de tractats d'estadística i permeten calcular les probabilitats de qualsevol altra distribució normal emprant la propietat que es comentarà seguidament. Tot i que amb el programari iestadístic d'ordinador (l'Excel en el nostre cas) no cal fer servir la distribució normal estàndard com a auxiliar per a altres càlculs, és important conèixer-la, ja que té importants aplicacions conceptuals.
Adoneu-vos que, com sempre, el procés d'estandardització transforma la distribució en una altra de mitjana 0 i desviació estàndard 1, però, en aquest cas, a més, transforma una distribució normal en una altra del mateix tipus. Aquesta és una propietat fonamental a l'hora de caracteritzar una distribució normal. |
|||||
|
|
Aproximació de la distribució binomial mitjançant la normal | ||||
| Ja s'ha dit que el càlcul
de les probabilitats corresponents a la distribució
binomial B(n,p) no es pot fer a mà (ni directament
amb l'ordinador) si n és (molt) gran. Durant molt de temps
es va cercar un model matemàtic que permetés obtenir els valors
de la distribució binomial de manera àgil també
si n és gran. A més de permetre estudiar les distribucions
derivades de mesures reals, la distribució normal també aconsegueix
aquest objectiu.
Es pot observar empíricament que en moltes ocasions la distribució normal dóna una bona representació dels valors de la distribució binomial B(n, p) que té la mateixa mitjana i la mateixa desviació estàndard. Aquesta constatació es fa des del punt de vista gràfic a la pràctica 3 d'aquest mòdul i també des del numèric a l'exercici 4. Hi ha una qüestió conceptual molt important que cal comentar abans d'assegurar que podem aproximar els valors de la distribució binomial mitjançant els valors de la distribució normal.
Feta aquesta precisió, convé concretar en quines condicions es pot dir que l'aproximació és correcta: s'ha de complir que np i també nq siguin grans. La bondat de l'ajustament anirà millorant a mesura que augmentin aquests valors.
La consideració d'aquesta aproximació de la distribució binomial mitjançant la distribució normal no canvia pas el tipus de problemes en què escau la distribució binomial, només la forma de calcular-ne els valors de manera més àgil i còmoda i, en concret, la possibilitat de calcular-los efectivament. |
|||||
|
|
La distribució exponencial | ||||
Recordeu que la distribució geomètrica modelitza l'experiment que compta quantes vegades hem de repetir una prova per observar un èxit en la realització de determinat fenomen. A diferència dels exemples típics de la distribució geomètrica, com és ara el recompte de tirades d'un dau fins que traiem un 5 o el nombre de cotxes que han de passar fins que en veiem un de color vermell, en determinades experiències la prova pot consistir a deixar passar un període de temps i veure si succeeix alguna cosa. I en el límit, quan passem d'intervals de temps discrets a l'evolució contínua del temps, ens pot interessar constatar en quin instant passa alguna cosa. Així, arribem a la distribució exponencial. Algunes situacions reals en què escau la distribució exponencial són les següents: l'estudi del temps que duren les piles elèctriques; l'interval de temps entre vehicle i vehicle en una carretera amb trànsit lliure; el temps que passa entre dues comunicacions d'una malaltia infecciosa que s'escampa de manera aleatòria per una població; el temps de vida de les partícules d'un material radioactiu... Totes aquestes situacions estan caracteritzades pel fet de correspondre
a la mesura d'una durada (...fins que passa alguna cosa); com a
tal mesura, els seus valors corresponen a una distribució contínua.
En tots els casos, allò que caracteritza la distribució
és la mitjana d'allò que estudiem.
Per exemple, si s'ha comprovat estadísticament que la durada mitjana de les piles elèctriques d'un tipus és de 100 hores, la funció de densitat de probabilitat relativa a aquesta experiència és f(x) = 0,01 · e – 0,01x. La distribució exponencial permet un càlcul manual (amb calculadora científica) relativament eficaç... però, tanmateix, com en el cas de les altres distribucions contínues presentades, l'Excel facilita eines per a l'estudi d'aquesta distribució:
Ara bé, a l'hora de veure si un conjunt de dades recollides correspon a la distribució exponencial, hem de conèixer el perfil de la funció de densitat d''aquesta distribució del qual a la pràctica 5 se'n dóna la visió gràfica i que, naturalment, té un grau de similitud molt gran amb el diagrama de barres de probabilitat de la distribució geomètrica:
Si s'observen aquestes característiques, estem en situació d'assajar un contrast de les dades recollides amb el model exponencial. |
|||||
| Ampliacions, aclariments i comentaris | |||||
|
|
Com a idea inicial començarem suposant que s'ha dividit el rang de valors de la variable X en sotsintervals molt petits, de longitud dx cadascun d'ells. Per a tots els punts d'un d'aquests intervals, posem per cas el que
té per centre x, es pot suposar que el valor de f(x)
és constant i, llavors, la probabilitat que el valor de X
resulti ser d'aquest interval serà f(x)·dx
i, llavors, a la definició de mitjana, en lloc del sumatori de
Finalment, si pensem que els intervals són infinitament petits, el càlcul d'aquesta darrera suma ens porta de ple al càlcul integral i, per això, i per raonaments semblants per als altres paràmetres, per a una distribució contínua amb funció de densitat de probabilitat y = f(x) es defineixen:
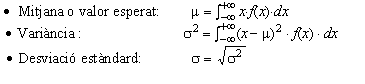
|
||||
|
|
Ja sabeu que
els valors de la funció de densitat de probabilitat no són
probabilitats, sinó que és l'àrea sota la corba la
que dóna la probabilitat; tanmateix, és interessant constatar
aquesta coincidència
Les figures següents il·lustren la quasi coincidència
dels valors de p[k–0,5 La probabilitat de l'interval [k–0,5, k+0,5] és l'àrea ombrejada en la figura de l'esquerra, on la línia més gruixuda representa la gràfica de la funció y = f(x).
Aquesta àrea es pot considerar pràcticament igual, en les situacions que ens interessen, a la del rectangle ombrejat a la figura de la dreta. Ara bé, aquest rectangle té:
i, per tant, el valor numèric de l'àrea d'aquest rectangle coincidirà amb el valor f(k). |
||||
|
|
La distribució exponencial permet un càlcul manual (amb calculadora científica) relativament eficaç El càlcul integral permet establir una fórmula per a la funció de distribució (de probabilitat acumulada) de la distribució exponencial. Com que aquesta distribució només es considera per a valors positius, en què f és la funció de densitat i F la funció de distribució, és: 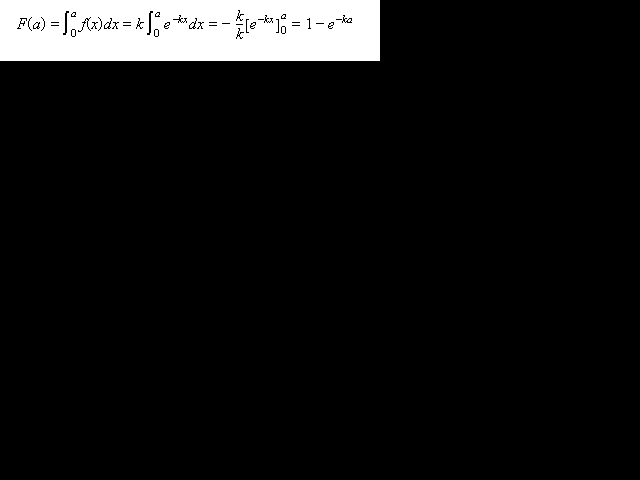
I d'aquí la funció de distribució (probabilitat acumulada) de la distribució exponencial és:
I semblantment per a la qüestió:
Cal calcular F(100) – F(75) i passar la resposta a tant per cent. A l'exercici 2 us demanem que feu càlculs en una situació pràctica que correspon al model exponencial. Ara ja sabeu que ho podeu fer amb la calculadora científica, però, tanmateix, us recomanem que arribeu al resultat amb l'Excel.
|
||||