En aquesta pràctica es proposen algunes petites investigacions al voltant de la geometria del triangle, per tal d’exercitar l’habilitat de construir configuracions i per tastar la satisfacció que produeixen els resultats.

Activitats

Si P és un punt del pla i ABC és un triangle, les rectes AP, BP i CP s'anomenen les cevianes de P.

Les mitjanes, les altures i les bisectrius són exemples de cevianes.

Tres cevianes tallen als costats (o a les seves prolongacions) en tres punts, que formen un nou triangle anomenat triangle cevià de P. 

Obriu i manipuleu la figura TRICEVIA.FIG. Us sembla que el triangle cevià sempre és interior a ABC? (proveu de fer sortir P a fora...) Sabeu quin és el triangle cevià del baricentre?
 
 

2. Les isogonals

Dues rectes que passen per un vèrtex d’un triangle són isogonals si els angles que cada una forma amb el costat més proper dels que surten del vèrtex són dos angles iguals.

Obriu i manipuleu la figura ISOGONAL.FIG.

Per construir la recta isogonal a una donada és suficient fer la seva simètrica respecte de la bisectriu.

Exercici 7

Comproveu la bonica propietat: les isogonals de tres cevianes són tres cevianes.

Trobareu còmode emprar la macroconstrucció que heu preparat a l’exercici 7. Si no l’heu fet, us haureu d’entretenir construint les isogonals d’una en una.

Els punts de concurrència de dos conjunts de cevianes isogonals s’anomenen punts conjugats isogonals.

Exercici 8 

Les rectes isogonals de les mitjanes s’anomenen les simedianes i el seu punt de concurrència és el simedià. És un dels punts amb més propietats de la geometria del triangle.
 
 

3. El triangle pedal

Si P és un punt del pla i ABC és un triangle, les projeccions ortogonals de P sobre els costats d'un triangle o les seves prolongacions formen un nou triangle que s'anomena el triangle pedal de P respecte ABC.

Obriu i manipuleu la figura PEDAL.FIG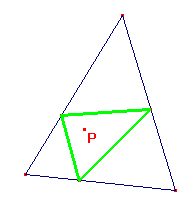

El més important dels triangles pedals és aquell en què P és l'ortocentre; els vèrtexs del triangle pedal són els peus de les altures, i el triangle pedal s'anomena triangle òrtic.

La seva propietat més important és: el triangle òrtic d’un triangle ABC és el triangle de perímetre mínim inscrit en ABC.

Obriu la figura ORTIC.FIG  i comproveu aquesta propietat. El segment inferior és el perímetre mínim, i el superior és el perímetre del triangle inscrit que pot moure’s lliurement per dins de l’altre.

Podeu trobar un parell de demostracions clàssiques d’aquesta propietat al llibre de H. Rademacher i O. Toeplitz citat a la bibliografia

A partir d’ara podeu emprar la macro TRI_ÒRTIC.MAC per investigar algunes propietats del triangle òrtic.

Exercici 9
 
 

4. La circumferència dels nou punts

La circumferència dels nou punts (o de Feuerbach) associada a un triangle és la circumferència circumscrita al triangle medial.

Dibuixeu-la (recordeu-vos de les macros que teniu disponibles).

Afegiu a la figura l’ortocentre i els punts mitjans entre l’ortocentre i els vèrtexs (que s’anomenen els punts d’Euler)

Us quedarà una figura semblant a aquesta: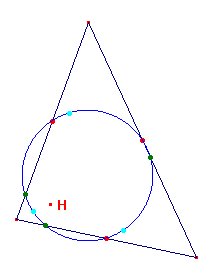

La circumferència dels nou punts és molt corrent en geometria del triangle. S’anomena “dels nou punts” perquè conté els tres punts mitjans dels costats, els tres peus de les altures i els tres punts d’Euler, però en realitat hi ha fins a 44 punts “notables” del triangle que estan sobre aquesta circumferència!!

A partir d’ara podeu emprar la macro CIRC_9_PUNTS.MAC

Exercici 10
 
 
 
 

Resum

 

En aquesta pràctica heu d'aprendre: (A) Que al voltant d'un triangle es poden construir molts objectes associats (B) A desenvolupar la vostra capacitat d'observació i d'investigació.

Comentaris al marge

1. El paper dels teoremes de Desargues i de Pappus és crucial en l’algebraització de la geometria. A grans trets, el teorema de Desargues correspon a la propietat associativa i el teorema de Pappus a la propietat commutativa.

2. Aquests dos teoremes controlen el curiós tema de les construccions amb elements inaccessibles. Per exemple: com traçar la recta que passa per dos punts si en mig d'ells hi ha una zona que no es pot utilitzar per al dibuix?

3. Encara que sembli difícil de creure, dos triangles qualssevol poden moure’s fins que quedin en perspectiva. Això es pot comprovar amb Cabri-Géomètre, però donar-ne un procediment de construcció no és elemental. Si algú ho vol provar...