|
RECTES NOTABLES I PUNTS EXCEL·LENTS
La part més coneguda de la geometria del triangle és la que es refereix a les diverses rectes i punts que s’hi poden determinar amb propietats especials. En aquesta pràctica comença l’estudi dels més elementals.
|
||
 |
Activitats1. Les mitjanesLes mitjanes d’un triangle són els segments (tot i que a vegades reben el mateix nom les rectes que els porten) que uneixen cada vèrtex i el punt mitjà del costat oposat. Dibuixeu un triangle i les seves tres mitjanes. Observareu que són concurrents. Aquesta concurrència és una relació conclusiva en el sentit del mòdul 2 .Comproveu que es tracta d’un invariant. El punt de concurrència de les tres mitjanes s’anomena baricentre. El baricentre divideix les mitjanes en dues parts, una de les quals
té longitud doble de l’altra. Podeu idear una comprovació
d’aquesta propietat, dins de Cabri-Géomètre, que no passi
per mesurar segments?
2. Les altures Les altures d’un triangle són les rectes que passen per un vèrtex i són perpendiculars al costat oposat. Dibuixeu un triangle i les seves tres altures. Demostreu, com abans,
que són concurrents.
3. Les mediatrius Dibuixeu un triangle i les mediatrius dels seus tres costats, i demostreu dinàmicament que són concurrents. El punt de concurrència s’anomena el circumcentre. Traceu la circumferència que té per centre el circumcentre
i que passa per un vèrtex. Aquesta és la circumferència
circumscrita al triangle.
4. Les bisectrius Dibuixeu un triangle i les bisectrius dels seus tres angles, i demostreu dinàmicament que són concurrents. El punt de concurrència s’anomena l’incentre. Traceu la circumferència que té per centre l’incentre i que passa per la projecció ortogonal de l’incentre sobre un costat. Aquesta és la circumferència inscrita en el triangle. Obriu la figura BISEXT.FIG. Hi figuren les tres bisectrius dels angles exteriors del triangle ABC. 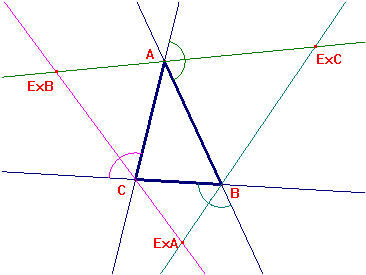 Traceu les bisectrius d’ABC i descriviu la propietat de concurrència
que observeu.
Tot i que és una mica entretingut, traceu les circumferències de centre EA, EB i EC i que passin per les respectives projeccions ortogonals d’aquests tres punts sobre el costat més proper. Aquestes són les circumferències exinscrites al triangle. Com el seu nom indica, els excentres d’un triangle són a l’exterior d’aquest. Investigueu què passa amb els altres punts: Exercici 4 El triangle que es forma unint els punts mitjans dels costats d’un triangle s’anomena el triangle medial del triangle original. L’incentre del triangle medial s’anomena el punt de Spieker.
5. Relacions importants Entre aquests punts hi ha algunes relacions interessants. La recta que enllaça el circumcentre, el baricentre i l’ortocentre d’un triangle s’anomena la recta d’Euler. La recta que enllaça l’incentre, el baricentre i el punt de Spieker
d’un triangle s’anomena la recta de Spieker.
_________________________________________________________________
Aclariments i notes tècniques
Tot i que el traçat de les rectes i dels punts notables sigui conceptualment senzill, pot resultar feixuc si cal fer-lo molt sovint. Les macroconstruccions són ideals per reduir la feina. Us les podeu fer a mida, però per si de cas hi ha algunes que ja estan a punt. Les trobareu a la carpeta Macros del material del curs. El seu nom ja indica de què s'encarrega cada una.
Atenció: les macros que s’apliquen a un triangle requereixen
que aquest hagi estat creat amb l’eina Triangle i no com un conjunt de
tres segments.
Resum
|