PRÀCTICA

 

QUADRILÀTERS INSCRITS I CIRCUMSCRITS


Una prolongació natural de la geometria de triangles és l’estudi de la relació entre quadrilàters i circumferències (inscripció i circumscripció). Els resultats no són tan universals com en el triangle, però tenen molt d’interès.

 

Activitats


1. Quadrilàters inscrits

Per tres punts no alineats passa una circumferència, però per quatre punts això no sempre és possible. Quan és així els punts s’anomenen concíclics i el quadrilàter que els té per vèrtexs és un quadrilàter inscrit.

Preneu una circumferència i quatre punts sobre ella. Són punts concíclics. Mesureu els quatre angles del quadrilàter inscrit que formen.

Analitzeu la suma dels angles oposats.

El motiu d’aquest resultat es veurà al mòdul 4, pràctica 2 
 
 

Un quadrilàter és inscrit si els parells d’angles oposats tenen la 
 mateixa suma.

Equivalentment, un quadrilàter és inscrit si la suma de productes de costats oposats és igual al producte de les diagonals (teorema de Ptolomeu)

Els rectangles, quadrats, trapezis isòsceles i estels rectangles són quadrilàters inscrits. Comproveu-ho.

Exercici 14
 
 

2. Els quadrilàters circumscrits

En tot triangle es pot inscriure una circumferència, però això no és cert per a tot quadrilàter. Si és així, el quadrilàter és un quadrilàter circumscrit.

Obriu la figura QCIRCUM.FIG.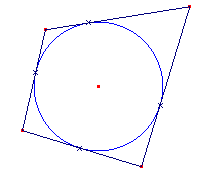

Analitzeu la suma dels costats oposats.

Traceu les bisectrius dels quatre angles del quadrilàter circumscrit.
 
 

Un quadrilàter és circumscrit si els parells de costats oposats tenen la mateixa suma.

Equivalentment, un quadrilàter és circumscrit si les bisectrius dels quatre angles són concurrents.

Els quadrats, els estels i els rombes són quadrilàters circumscrits. Comproveu-ho.
 
 

3.  Els quadrilàters bicèntrics

Un quadrilàter que és alhora inscrit i circumscrit s’anomena quadrilàter bicèntric. Tenen les propietats dels inscrits i dels circumscrits. Obriu la figura BICENTRIC.GIF

Comproveu altres propietats addicionals:
  • Si MNPQ és el quadrilàter format pels punts de contacte amb la circumferència inscrita, llavors MNPQ té les diagonals perpendiculars
  • Les diagonals d'ABCD i les de MNPQ es tallen al mateix punt
  • Aquest punt està alineat amb I i O
  • Si ABCD és un estel, MNPQ és un trapezi isòsceles i recíprocament
Com s'ha construït? Vegeu l’Exercici 15 
 
 
 

Resum

       
      En aquesta pràctica heu d'aprendre:

      (A) Les propietats dels quadrilàters inscrits 

      (B) Les propietats dels quadrilàters circumscrits

      (C) Les propietats dels quadrilàters bicèntrics.