La posició d’un angle respecte d’una circumferència relaciona la mesura de l’angle amb els arcs que determina en ella. Com a conseqüències es pot construir l’angle corresponent a un arc, i resoldre un problema antic per mitjà de Cabri-Géomètre.

Activitats

1. La mesura d'un arc

Un arc és la porció de circumferència compresa entre dos dels seus punts. Dos punts d’una circumferència determinen dos arcs.

Si no es diu res en contrari, l’arc designat pel nom de dos punts serà el menor dels arcs que determinen.

La mesura d’un arc és la de l’angle que té el vèrtex en el centre de la circumferència i els costats del qual passen pels extrems de l’arc. Un angle d’aquest tipus és un angle central.
Exercici 3
 

2. Posició dels angles respecte la circumferència

Obriu la figura ANGCIR.FIG.

L’angle ACB és un angle inscrit que abasta l’arc AB. Comproveu que la mesura de l’angle inscrit és la meitat de la mesura de l’arc AB que abasta.

En particular, un angle inscrit que abasta una semicircumferència és un angle recte.

L’angle GPE és un angle exterior a la circumferència. La seva mesura depèn de les dels arcs GE i DF. Investigueu de quina manera.

L’angle HQI és un angle interior a la circumferència. La seva mesura depèn de les dels arcs HI i JK. Investigueu de quina manera.

L’angle de vèrtex R, format per una secant a la circumferència i per una tangent és un angle semiinscrit a la circumferència. La seva mesura depèn de la de l’arc SR. Investigueu de quina manera.
 

.
3. L'arc capaç

Donat un angle  i dos punts A i B, pot buscar-se l'arc que tingui extrems A i B i tal que els angles inscrits en ell amb costats que passin per A i per B siguin iguals a  . Aquest és l’arc capaç de l’angle .

Per traçar l'arc capaç cal fer:
a) Traceu la mediatriu m d’AB.
b) Transporteu l’angle  de forma que el vèrtex quedi a B, i que AB sigui un costat. Es crearà una recta r.
c) Traceu la recta s perpendicular a la recta r per B.
d) Dibuixeu el punt O d’intersecció entre s i m.
e) Traceu la circumferència de centre O que passa per A i per B.
f) Creeu l'arc "gran" delimitat per A i B

Exercici 4

L’arc capaç intervé en nombroses construccions geomètriques en què una dada és un angle però es desconeix el seu vèrtex.
 

4. La trisecció de l'angle

Un dels problemes més coneguts de la geometria grega és el problema de la trisecció de l’angle, és a dir, de la seva divisió en tres parts iguals. Aquest problema no té solució amb regle i compàs, però sí dins de la geometria dinàmica.

Obriu la figura TRISEC.FIG. Aquesta figura està construïda així: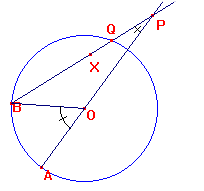

(1) l'angle AOB que es vol dividir es posa com a angle central en una circumferència
(2) es pren un punt arbitrari P en la recta AO
(3) es traça la recta BP
(4) sobre aquesta recta es trasllada un segment PX igual al radi de la circumferència.

Ara:

(5) es desplaça P fins que X coincideixi amb el punt Q en què BP talla la circumferència
(6) en tal situació, l'angle BPO és la tercera part de l'angle AOB.

La construcció és rigorosament euclidiana excepte el pas (5), que pertany a la geometria dinàmica.
Comproveu que el resultat de la trisecció és correcte. 

La justificació del resultat la fareu com a Exercici 5

Tot i que Cabri-Géomètre es presti admirablement a aquesta construcció de la trisecció, cal notar que Arquímedes ja la coneixia.
 
 
 

Resum

 

En aquesta pràctica heu d'aprendre: (A) A mesurar un arc (B) Les relacions dels angles i la seva mesura amb els arcs de circumferència (C) La construcció de l'arc capaç.