Sembla que de dues circumferències secants no es pot dir gran cosa. Però susciten la mateixa pregunta que les rectes secants. Quin angle formen? Què passa quan aquest angle és recte?

Activitats

1. Angle entre dues circumferències

És l'angle entre les tangents en els punts d'intersecció. És indiferent en quin dels dos punts d'intersecció es calculi; té el mateix valor.

Obriu la figura CIRCANG.FIG i adjunteu-hi la mesura de l'angle marcat. Modifiqueu les circumferències fins que aquest angle sigui de 90º. Per on passen llavors les dues tangents?

Les circumferències que formen un angle recte són circumferències ortogonals.

Per construir-les es necessita determinar-les amb algunes dades addicionals. Un dels casos és:

Construir una circumferència ortogonal a una donada, sabent el punt de tall A i que la circumferència demanada passa per B.

La construcció corresponent està feta en la figura CIRCORT.FIG. És de suposar que l'entendreu només mirant-la.

2. Circumferència ortogonal a dues o a tres

Heu vist a l'exercici 15 que per a cada posició del centre podeu traçar una circumferència ortogonal a C1. Hi ha alguna posició del centre tal que la circumferència també sigui ortogonal a C2?

Obriu la figura CIRCORT2. FIG. Les circumferències D i C1 són ortogonals. Moveu P fins que D també sigui ortogonal a C2. Traceu llavors l'eix radical  de C1 i C2. Què observeu?
 
 

 Per tant, si es vol construir una circumferència D ortogonal a tres circumferències C1, C2 i C3, és clar que el seu centre ha de ser el centre radical de C1, C2 i C3. Traçant les tangents des d'ell a una de les tres, els punts de contacte són punts de la circumferència D.  Observeu-ho a la figura CIRCORT3.FIG.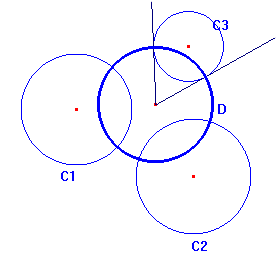

3. Determinació per dos punts: el disc de Poincaré

Donats dos punts A i B interiors a una circumferència C, és possible construir la circumferència ortogonal a C que passi per A i per B. La justificació d'aquesta construcció pertany al proper mòdul.

A la figura RECTHIP.FIG teniu l'arc d'aquesta circumferència ortogonal comprès a dins de C. Observeu el comportament d'aquest arc al modificar A i B.

Podeu prendre tres punts a l'interior de C i construir un triangle hiperbòlic. Compteu per fer-ho amb la macroconstrucció RECTA_HIPERB.MAC. Quan tingueu un d'aquests triangles mesureu els tres angles i calculeu la seva suma.
 
 
 

Resum

 

En aquesta pràctica heu d'aprendre: (A) El concepte de circumferències ortogonals  (B) Algunes construccions de circumferències ortogonals (C) El model del disc de Poincaré per a la geometria hiperbòlica.