|
TANGÈNCIES
La posició relativa de recta i circumferència, i la de dues circumferències entre elles, motiva una gran quantitat de tècniques i de resultats relacionats sobretot amb la relació de tangència. Per això aquesta pràctica és bastant llarga.
|
|||||||||
 |
Activitats1. Posicions recta-circumferènciaUna recta i una circumferència poden estar en tres posicions relatives. Obriu la figura RECTAN.FIG. Hi veureu una recta, una circumferència i dos segments d i r. El segment r és el radi de la circumferència, i el segment d és la distància de la recta al centre de la circumferència. Moveu la recta agafant el punt X i mireu com va canviant el segment d. Veureu que la recta passa per tres posicions, que són:
2. La tangent a una circumferència en un dels seus punts El traçat de la recta tangent a una circumferència per un punt d’aquesta es fa utilitzant la propietat anterior. De tota manera, serà bo que l’automatitzeu i us en feu una macroconstrucció; us servirà tot seguit. Recíprocament, no hi ha cap dificultat en construir una circumferència
tangent a una recta donada. Una mica més interessant és l’
l’Exercici 6
3. Les tangents per un punt exterior Per un punt exterior a una circumferència es poden traçar
dues tangents a ella.
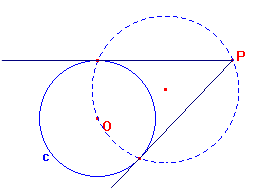 Analitzeu les relacions constitutives de la figura, tenint en compte
que els objectes simples són la circumferència c i el punt
P, i formuleu un mètode de construcció de les tangents a
una circumferència per un punt exterior. Penseu també perquè
funciona el mètode.
4. Hexàgons inscrits i circumscrits Un polígon que té tots els costats tangents a una circumferència és un polígon circumscrit a aquesta. Ja coneixeu els triangles i els quadrilàters circumscrits des dels mòduls anteriors. Ara, però, treballareu amb un hexàgon circumscrit. Serà a l’Exercici 7. De forma semblant, un polígon que té tots els vèrtexs en una circumferència és un polígon inscrit en aquesta. Treballeu amb un hexàgon inscrit a l'Exercici 8 Us pot semblar que aquest exercici no té res a veure amb el tema de les tangents. Si penseu això, la vostra intuïció us ha fallat! Preneu una circumferència i un punt P exterior a ella. Traceu tres secants per P a la circumferència i apliqueu el teorema de Pascal als sis punts de tall. La recta dels punts d’intersecció que resulta del teorema talla la circumferència en dos punts. Uniu-los amb P i observeu...
5. Posicions de dues circumferències Dues circumferències poden estar en cinc posicions relatives. Obriu la figura CIRTAN.FIG. Hi veureu dues circumferències i cinc segments. Dos dels segments porten els noms r i s, i representen els radis de les dues circumferències. El segment d és la distància entre els centres de les dues, i els altres dos són les diferències que estan indicades. D'entrada les circumferències no estan en contacte: diem que són exteriors. Si preneu el centre de la circumferència gran i l’aneu movent cap a l'altra, les circumferències passaran a ser, successivament: tangents exteriors, secants, tangents interiors i interiors. 6. Tangents comunes Donades dues circumferències exteriors és possible traçar dos jocs de rectes (quatre en total) que siguin tangents a les dues: són les tangents exteriors comunes (en vermell a la figura) i les tangents interiors comunes (en verd a la figura). Si les circumferències són secants, només existeix el parell de tangents exteriors comunes.
Els punts on es talla cada parell de tangents s’anomenen els centres d’homotècia de les dues circumferències. Per traçar les tangents comunes és suficient prendre dos diàmetres, un a cada circumferència, que siguin paral·lels, i traçar les rectes que passen pels extrems d’aquests diàmetres. Aquestes rectes es tallen en els centres d’homotècia. Les macroconstruccions TANG_EXT_COMUNES.MAC i TANG_INT_COMUNES.MAC ho faran tots els cops que vulgueu. Exercici 10
Exercici 11
Exercici 12
La construcció de circumferències per condicions de tangència és un tema molt vast i que es concentra en l’anomenat Problema d’Apol·loni. Feu-ne un tast amb l’ Exercici 13, que és
el darrer de la pràctica.
Resum
Comentaris al marge A. Els teoremes de Pascal i de Brianchon pertanyen a la geometria projectiva i, en el llenguatge d’aquesta, són duals l’un de l’altre. Són vàlids per a qualsevol cònica que no sigui la circumferència. En especial el teorema de Pascal es pot formular per a la cònica degenerada formada per dues rectes; llavors és el teorema de Pappus que s’ha vist al mòdul 2, pràctica 3 El teorema de Pascal té propietats inesperades. Amb els sis punts que heu posat a la circumferència podeu formar 60 hexàgons diferents (feu un senzill raonament de combinatòria per confirmar-ho). Si la recta on estan els punts d’intersecció dels costats oposats l’anomeneu recta de Pascal de l’hexàgon, resulta que els sis punts produeixen 60 rectes de Pascal. Les rectes de Pascal són concurrents de 3 en 3 en 20 punts anomenats punts de Steiner, i cada recta de Pascal conté un punt de Steiner. Els punts de Steiner estan alineats de 4 en 4 en 15 rectes anomenades rectes de Plücker, i hi ha 3 punts de Steiner a cada recta de Plücker. Les rectes de Pascal són concurrents també de 3 en 3 en 60 punts anomenats punts de Kirkman, i cada recta de Pascal conté tres punts de Kirkman. Els punts de Kirkman estan alineats de 3 en 3 en 20 rectes anomenades rectes de Cayley, i a cada recta de Cayley hi ha tres punts de Kirkman i un punt de Steiner. Les rectes de Cayley són concurrents de 4 en 4 en 15 punts anomenats
punts de Salmon...
B. La construcció de les tangents a partir del teorema de Pascal que es fa en el punt 4 de la pràctica pot semblar innecessàriament complicada. Penseu, però, que és una construcció projectiva (no fa servir més que el regle) i vàlida per a totes les còniques. Podeu provar de fer-la amb llapis i regle sobre alguna hipèrbola o paràbola que tingueu impressa en paper. La tornareu a veure a la pràctica 4 del mòdul 5. |