La relació d'harmonia entre punts alineats és difícil de captar visualment però té una gran importància en geometria, començant pel concepte de polaritat.
 

Activitats

Si A, B, C i D són quatre punts alineats, el parell (A, C) és conjugat harmònic del parell (B, D) si AD·BC = AB·CD. 

Obriu la figura HARMON1.FIG i veureu un exemple. Desplaceu els punts A, B i C per observar les posicions relatives dels quatre punts.

A la figura la comprovació de la relació és purament numèrica i no té cap component visual. Aquest es pot obtenir canviant la condició per    i recordant la proporcionalitat. 

Obriu la figura HARMON2.FIG i trobareu quatre punts alineats. "Desplegueu" la figura movent els punts que hi ha per sota d'A i obtindreu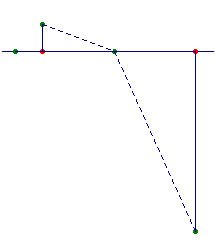

Moveu lliurement A, B, C i D fins que ho estiguin. Si voleu una comprovació numèrica, feu-la prenent les longituds dels segments amb Distància i longitud del grup Mesures.

I parlant de relacions numèriques, cal dir que el nom de "punts harmònics" prové de què la longitud AC és la mitjana harmònica de les longituds AB i AD.
 

2. La construcció del quart harmònic

Donats A, B i C, la construcció de D s'anomena la construcció del quart harmònic. Es pot fer emprant només el regle, tot i que la construcció que s'explica a continuació és més breu.

Obriu la figura HARMON3.FIG i la veureu. 

Els seus passos són:
(1) Es pren una recta qualsevol que passi per A, i M sobre ella
(2) Es traça la paral·lela a la recta AM que passa per C
(3) Es traça MB que talla la recta anterior en U
(4) Es pren el simètric V de U respecte C
(5) La recta MV talla la recta d'A, B i C en el punt D.

En el futur us farà la construcció la macro QUART_HARMÒNIC.MAC, clicant la recta on són els punts A, B i C, després el parell A, B i C.

Una de les propietats més notables d'aquesta relació és la seva invariància per projecció de qualsevol tipus. Això la fa una relació més forta que la proporcionalitat, que només és invariant per projecció paral·lela (teorema de Tales).

Per comprovar-ho obriu la figura HARMON4.FIG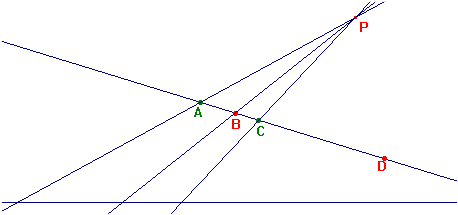

Els punts A, B, C i D formen un conjunt harmònic. Projecteu A, B i C a partir de P sobre la recta inferior, i busqueu el quart harmònic de les tres projeccions emprant la macro. Veureu que és la projecció de D.

Aquesta propietat fa de la relació de conjugació harmònica un dels fonaments de la geometria projectiva.

I, sense arribar tan lluny, podeu comprovar vosaltres mateixos que apareix en dues situacions que ja coneixeu:

• Dos vèrtexs B i C d'un triangle són harmònics respecte els punts on les bisectrius interior i exterior de l'angle A tallen la recta BC.
• Els centres de dues circumferències són harmònics respecte els seus dos centres d'homotècia.

Obriu la figura POLAR1.FIG. Hi veureu un punt P, una circumferència i una recta per P que és secant a la circumferència en X i Y.

Utilitzant la macro QUART_HARMÒNIC, construïu el punt Q tal que (X,Y) i (P,Q) són conjugats harmònics (cliqueu la secant, X, P i Y en aquest ordre).

Dibuixeu tres secants més per P i repetiu el procés. Comproveu que tots els "punts Q" estan alineats.

La recta que formen s'anomena la polar de P respecte de la circumferència, i recíprocament P s'anomena el pol de la recta respecte de la circumferència.

Obriu la figura POLAR3. Hi veureu un punt P i una recta r: el punt P és el pol de la recta r, i la recta r és la polar de P. Moveu la recta r i observeu com varia la posició de P, segons si r és exterior, secant o tangent a la circumferència. Mireu d’adquirir una mena de percepció - familiarització amb les posicions del pol i la polar.

Ara obriu la figura POLAR2. Us semblarà igual que l'anterior, però ara és P (el pol) qui es pot moure, i r (la polar) la que el segueix. Moveu el punt P i observeu com varia la posició de r.

Què passa si P s'aproxima al centre de la circumferència? Què creieu que passarà quan P estigui just al centre?

Observeu també una propietat:

La polar d'un punt respecte una circumferència és perpendicular a la recta que passa pel punt i pel centre de la circumferència.

La construcció de la polar es va veure a la secció 4 de la pràctica 3 del mòdul 4 : és la recta en vermell. A partir d'ara podeu fer-la amb la macroconstrucció RECTA_POLAR.MAC.

També disposeu de la macro POL_RECTA.MAC, que us farà el pol d'una recta.

Utilitzeu-les per resoldre l'Exercici 10 
 
 
 

Resum

 

En aquesta pràctica heu d'aprendre: (A) El concepte de punts conjugats harmònics. (B) La construcció i les propietats dels punts harmònics. (C) La relació de polaritat entre punts i rectes.