Com aplicacions de la semblança de triangles, algunes construccions molt antigues i molt poc conegudes permeten en aquesta pràctica establir una àlgebra geomètrica dels segments.

Activitats

1. La suma de segments

Obriu la figura SUMA.FIG  i manipuleu-la. Veureu que efectua la suma de dos segments.

Aquesta activitat introdueix, per primera vegada en el curs, el concepte d'orientació; i ho fa per atribuir un signe a les quantitats representades pels segments. Aquests tenen l'origen en un eix vertical arbitrari i segueixen "cap a la dreta" (els positius) o "cap a l'esquerra" (els negatius).

De la mateixa manera es faria la diferència de segments.
 

2. La multiplicació de segments

Quant a la multiplicació, la teniu il·lustrada a la figura PRODUCTE.

0A té la longitud del segment a i 0B la del segment b; 01 té longitud unitat. Escrivint la proporcionalitat de costats entre els triangles semblants 01B i 0AC s’obté 0C = 0A·0B.

Manipuleu l’orientació d’a i b i observeu l’orientació d’ab. Tindreu una bonica il·lustració de les “regles dels signes”.

És clar que la divisió es fa amb una figura que és una senzilla variant d’aquesta. Feu-la a l’Exercici 8 
 

3. La radicació

L’altra operació entre segments que es pot fer per mitjà de la geometria és l’arrel quadrada, que és un cas particular de la construcció de la mitjana geomètrica entre dos segments.

Obriu la figura ARREL.FIG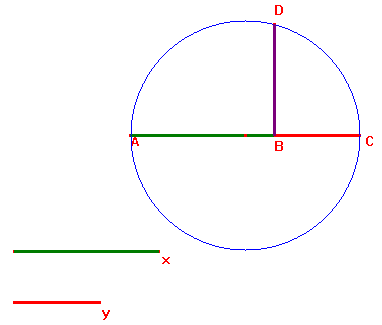

Penseu com s’ha construït la figura a partir dels segments x i y.

Traceu els segments AD i DC i apliqueu el teorema de l’altura al triangle ADC. Obtindreu immediatament que la longitud el segment DB és la mitjana geomètrica dels segments x i y, o sigui  .
Si preneu x de longitud unitat, obtindreu l'arrel quadrada de y.

I què us semblaria l’arrel cúbica? Recordareu que un dels problemes “impossibles” de la geometria grega s’anomena la duplicació del cub, és a dir, la construcció amb regle i compàs de  . Però la geometria dinàmica és més llesta que l'euclidiana (ja ho heu vist a la trisecció de l’angle, pràctica 2 del mòdul 4 )

Aquesta és la construcció, a partir d'un segment k, d'un altre segment x tal que x³ = 2k³.

Els passos que cal seguir són:
(1) es construeix un triangle equilàter ABC que tingui costat k
(2) es fa el punt D simètric de C respecte d'A
(3) es pren un punt P en la prolongació d'AB
(4) es busca la intersecció Q de DB i CP
(5) es trasllada k a partir de P, formant el segment PX
(6) es desplaça P fins que X coincideixi amb el punt Q
(7) en tal situació, el segment CX és el segment x buscat.

Mireu de reproduir la construcció pel vostre compte.
 

4. La resolució d'equacions

Una de les ocupacions més corrents dels estudiants d’àlgebra a secundària és la resolució d’equacions de primer i de segon grau. Totes dues activitats es poden fer molt bé geomètricament.

Com comprendreu, la resolució de ax+b = c essent x = (c-b)/a, una combinació de les construccions de la recta i la divisió permet resoldre geomètricament les equacions de primer grau.

I les de segon grau? És clar que es pot implementar la cèlebre fórmula, perquè totes les operacions parcials que la componen poden fer-se geomètricament, però això seria terriblement llarg. Observeu, però, el magnífic mètode de resolució següent:

Obriu la figura GRAU2.

Seguim considerant que un segment és positiu quan està orientat a la dreta de 0, i negatiu quan està orientat a l'esquerra de 0. 

Modifiqueu s i p lliurement i mireu què passa amb x1 i x2. És possible que x1 i x2 coincideixin? És possible que x1 i x2 desapareguin? És possible que un d'ells desaparegui i l'altre no?

I ara, penseu una mica! Exercici 9
 
 

Resum

 

En aquesta pràctica heu d'aprendre: (A) A multiplicar i dividir segments geomètricament (B) A resoldre equacions de segon grau geomètricament. (C) La possibilitat de construir l'àlgebra a partir de la geometria.

Comentaris al marge
 

La construcció mostrada en el punt 5 és una alternativa interessant a la idea corrent que la resolució gràfica d'una equació de segon grau implica la intersecció d'una recta i d'una paràbola.

S’atribueix a l'historiador escocès Thomas Carlyle (1795-1881) i es pot trobar desenvolupada a l'article "Carlyle Circles" de D.W. DeTemple, American Mathematical Monthly vol. 98 núm 2 (1991).