La principal aparició de segments proporcionals a la geometria es produeix per mitjà dels triangles semblants. Aquesta pràctica en mostra els motius i les variants.

Activitats

1. Triangles semblants

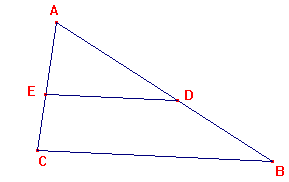
Dos triangles són semblants si tenen els angles iguals. Si a més a més els angles iguals poden superposar-se de forma que els costats que no els formen quedin paral·lels llavors són directament semblants.

Si dos triangles són semblants, els vèrtexs que corresponen a angles iguals s’anomenen vèrtexs homòlegs.

Obriu la figura TRISEM1. Moveu el triangle DEF, transportant-lo per D o per F, i superposeu-lo a ABC de forma que els vèrtexs D i A i els angles en aquests vèrtexs coincideixin. Observareu que són triangles directament semblants. 

Obriu la figura TRISEM2. Moveu el triangle DEF com en el cas anterior. Els dos triangles tenen els angles iguals? Quina diferència noteu amb el cas anterior?

Els triangles DEF i ABC són inversament semblants.

La propietat fonamental dels triangles semblants és:
 

La demostració d'aquesta propietat es fa per mitjà del teorema de Tales i val a dir que Cabri-Géomètre no hi pot ajudar gens.

En realitat, la definició clàssica de triangles semblants es fa per mitjà de la igualtat dels angles i de la proporcionalitat dels costats. Però aquestes sis condicions són excessives i poden reduir-se a tres condicions de quatre formes diferents; cada reducció s'anomena un "cas de semblança de triangles" 

Per tal de dibuixar un triangle DEF semblant a un triangle ABC, suposant que DE serà l’homòleg d’AB només cal transportar els angles A i B als extrems de DE. Feu-ho.

La semblança de polígons que no siguin triangles no és tan simple, perquè per a ells la igualtat d’angles no implica la proporcionalitat de costats.

Ho veureu a l’ Exercici 5
 

2. Construccions amb triangles semblants

Hi ha tres casos de construccions geomètriques simples que produeixen triangles semblants. 

• La primera d’elles és la secció d’un triangle per una paral·lela a un costat.

És clar que els dos triangles ABC i ADE són directament semblants. Però mireu l’ Exercici 6
 
•  La segona construcció és el traçat de l’altura d’un triangle rectangle que surt del vèrtex on hi ha l’angle recte.

 

 

Obriu la figura ALTURAD.FIG.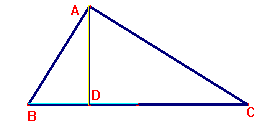

La figura conté tres triangles diferents. Alguns parells són directament semblants i alguns són inversament semblants. Identifiqueu-los.

Escrivint la proporcionalitat de costats homòlegs entre ABD i ADC es té .
Aquest és el Teorema de l’altura: en un triangle rectangle, l’altura que cau sobre la hipotenusa és mitjana proporcional entre les dues parts en què divideix a aquesta.

Una versió equivalent és AD·AD = DC·BD. 

Torneu a la figura ALTURAD.FIG, i desbloquegeu el vèrtex A amb l'eina Fixar/Alliberar del grup Aspecte. Un cop fet això desplaceu el punt A fins aconseguir un equivalent visual de la darrera igualtat.

Comproveu-la calculant l'àrea dels dos polígons de color amb l'eina Àrea del grup Mesures.
 

•  La tercera construcció és el traçat per un punt de dues secants a una circumferència. La veureu obrint la figura TRISEM4.FIG.

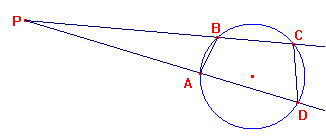Els triangles PAB i PDC són inversament semblants. Comproveu-ho. Escriviu la proporcionalitat de costats homòlegs i establiu la invariància de la potència d’un punt, segons heu vist a la pràctica 4 del mòdul 4

Resum

 

En aquesta pràctica heu d'aprendre: (A) A reconèixer les figures semblants (B) A construir figures semblants. (C) Les implicacions de la semblança de triangles com la invariància de la potència i el teorema de l'altura.

 
__________________________________________________

Comentaris al marge

 
En el triangle d'on s'ha tret el teorema de l'altura també es pot escriure la proporcionalitat de costats entre ABD i ABC, en la forma  . Aquest és el Teorema del catet: un catet és mitjana proporcional entre la hipotenusa i la seva projecció sobre aquesta.

El teorema del catet serveix per donar una demostració del teorema de Pitàgores. Per cert, ja que parlem d'aquest cèlebre teorema, aneu cap a l'Exercici 7