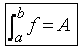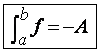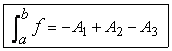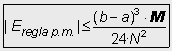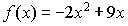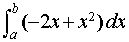|
INTRODUCCIÓ: OBJECTIUS |
|
|
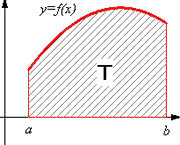
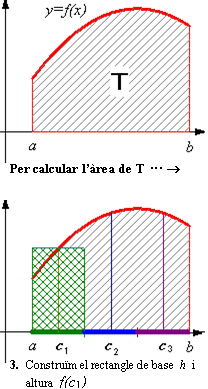
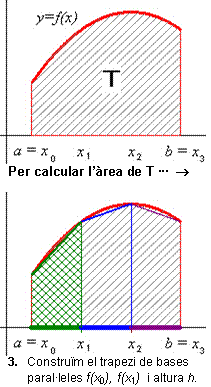
L'objectiu d'aquest capítol és que arribeu a entendre el concepte d'integral definida d'una funció i a calcular integrals de forma aproximada, per a la qual cosa us mostrarem primer com calcular, de manera aproximada, l’àrea de figures limitades per · la gràfica d’una funció y = f(x), · dues rectes verticals, x=a i x=b, i · l'eix OX. Les regions planes d’aquest tipus s’anomenen trapezis mixtilínis (regió T de la figura). |
|
En principi, n’hi ha prou que sàpigueu que “l’àrea d’una regió és el nombre de quadrats unitaris que hi caben en ella, i si la regió es ‘divideix en trossos’, l’àrea és la suma de les àrees de tales trossos”. Has de saber també que en els casos d’un rectangle i d’un trapezi de costats rectes, la superfície es calcula amb les fórmules següents (la 2a es pot deduir de la 1a; per comprovar-ho, clica en l’escena): |
|
|
|
FORMES D’APROXIMAR L’ÀREA DE TRAPEZIS MIXTILINIS |
|
1. Regla del punt mig |
|
|
|
|
|
|
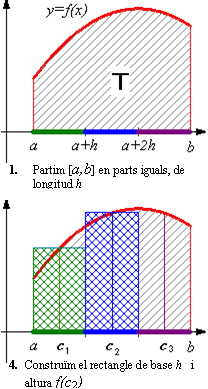
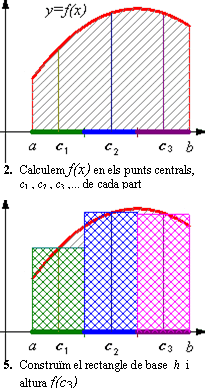
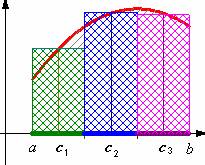
Els rectangles de l’última figura de la sèrie anterior, que reproduïm aquí, a l’esquerra, ens donen un valor aproximat de la superfície del trapezi mixtilini que volíem obtenir. Com tots aquests rectangles (3 en aquest cas) tenen base igual a h, la suma de les seves àrees ens dóna: h ·f(c1) + h ·f(c2) + h ·f(c3) = h · (f(c1)+ f(c2)+ f(c3) )
En general, si dividim l’interval [a,b] en N parts iguals, obtindrem la següent fórmula d’aproximació a l’àrea del trapezi mixtilini, coneguda com a regla del punt mig.
|
Quin error màxim ens podria donar la regla del punt mig?
|
Si f(x) és l’expressió d’una paràbola,
f(x) = Ax2+Bx+C, es pot demostrar que l’error absolut que ens donarà la regla del punt
mig mai no superarà el valor
D’aquesta fórmula es dedueix en quants intervals heu de dividir l’interval [a,b] per estar segurs que l’error obtingut no superarà un valor màxim tolerable E tolerat: Serà suficient obligar a què es compleixi |
|
|
|
2. Regla dels trapezis |
|
|
|
|
|
|
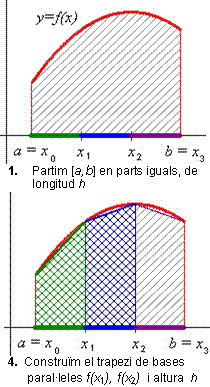
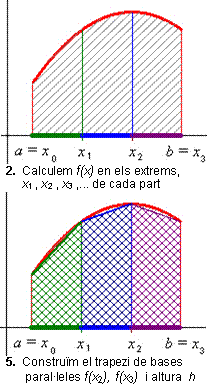
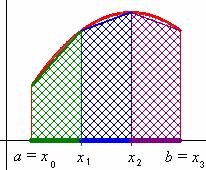
Els trapezis de l’última figura de la sèrie anterior, que reproduïm aquí, a l’esquerra, ens donen tots plegats un valor aproximat de la superfície del trapezi mixtilini que volíem obtenir. Com tots aquests trapezis (3 en aquest cas) tenen altura igual a h (recordeu que l’altura d’un trapezi és la distància entre els seus costats paral·lels), la suma de les seves àrees ens dóna la següent aproximació de l’àrea:
En general, si dividim l’interval [a,b] en N parts iguals, obtindrem la següent fórmula d’aproximació a l’àrea del trapezi mixtilini, coneguda com a regla dels trapezis:
|
Quin error màxim ens podria donar la regla dels trapezis?
|
Si f(x) és l’expressió d’una paràbola, f(x) = Ax2+Bx+C, es pot demostrar que l’error absolut que ens donarà la regla del
punt mig mai no superarà el valor
D’aquesta fórmula es dedueix en quants intervals heu de dividir l’interval [a,b] per estar segurs que l’error obtingut no superarà un valor màxim tolerable: E tolerat: Serà suficient obligar a què es compleixi |
|
|
|
RESUms |
|
Regla del punt mig · Si f és una funció contínua i positiva a l’interval [a,b], una aproximació de l’àrea del seu trapezi mixtilini és:
essent c1, c2,…, cN els punts centrals dels N intervals que resulten en dividir [a,b] en N parts iguals.
· Si
|
|
Regla dels trapezis · Si f és una funció contínua i positiva a l’interval [a,b], una aproximació de l’àrea del seu trapezi mixtilini és:
essent y0=f(x0), y1=f(x1), … , yn=f(xN), i on x0, x1, …, xN són els punts de divisió de [a,b] en N parts iguals.
· Si
|
|
Exercicis resolts |
|
1 |
Considera l’àrea sota la paràbola d’equació
En els dos casos, dibuixa l’àrea que serveix d’aproximació i indica l’error màxim comès. |
Resposta
|
|
|
En els dos casos, ordenarem els càlculs en forma de taula.
En el 1r cas, observa que els punts centrals dels intervals són 1/2, 3/2 i 5/2.
|
|
Per esbrinar el màxim error que podríem tenir en cada cas, apliquem la fórmula de l’error corresponent:
|
|
|
Cota d’error en regla del punt mig
|
Cota d’error en regla dels trapezis
|
|
2 |
Raona que la funció En quantes parts, com a mínim, hauríem de dividir l’interval [1,3] perquè, aplicant la regla del punt mig amb aquesta funció, tinguéssim la seguretat d’obtenir l’àrea del trapezi corresponent amb error menor que tres centèsimes? Després d’esbrinar-ho, calcula aproximadament tal àrea utilitzant el nombre de parts calculat. |
|
Resposta
|
Les solucions de Pel que fa al nombre mínim de parts que necessitem per assegurar un error màxim tolerable de 0,03, podem aplicar directament la fórmula
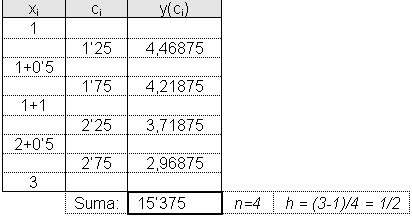
Per tant, hauríem de dividir en un mínim de 4 parts iguals l’interval [1,3] per estar segurs que obtindrem una aproximació amb error no superior a 3 centèssimes.
Càlcul de la aproximació
|
|
definició general d’àrea d’un trapezi mixtilini |
|
Pretenem ara definir l’àrea d’un trapezi mixtilini definit per la gràfica d’una funció acotada(*) i positiva, f, en un interval [a,b]. (Acotada significa que els seus valors, f(x), no poden ultrapassar una certa constant) Per fer-ho, dividim l’interval [a,b] en n subintervals (de longituds iguals o no). Siguin aquests intervals els següents: [x0,x1], [x1,x2], [x2,x3], …….., [xn-1,xn], on suposem x0=a, xn=b Si ara aixequem en els extrems de cada interval les ordenades fins a la corba, haurem dividit el trapezi mixtilini en “faixes” de amplituds (veure fig. 1): |
|
|
|
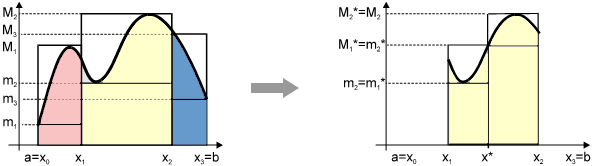
Mireu la figura 1 i les “faixes” que hem format. Si fem les horitzontals pels punts d’altures “màxima” i “mínima” de la corba en cada “faixa”, haurem format una sèrie de rectangles superiors i altra sèrie de rectangles inferiors. L’àrea de cada “faixa” quedarà compresa entre la dels seus rectangles superior i inferior, és a dir,
Llavors, si indiquem amb Sn la suma dels rectangles l’ordenada dels quals és màxima
i indiquem amb sn la suma dels rectangles l’ordenada dels quals és mínima
resulta evident que el que intuïtivament entenem per àrea del trapezi mixtilini quedarà entre les sumes Sn i sn , és a dir,
A més, si s’augmentéssim el nombre d’intervals dividint en parts els que n’hi ha, en cada una de les noves faixes disminuiria l’ordenada màxima Mi (o quedaria igual) i augmentaria l’ordenada mínima mi (o quedaria igual). Per tant, disminuiria la suma dels rectangles d’altura màxima i augmentaria la dels d’altura mínima. Podem comprovar l’afirmació anterior en la figura 2, on hem separat la faixa de l’interval [x1,x2], i hem partit aquest en 2 parts mitjançant un punt intermig x*. Es veu que M1*< M2 i M2*= M2 i, per tant, |
|
M1*·(x*-x1) + M2*·(x2-x*) < M2·(x*-x1) + M2·(x2-x*) = M2·(x2-x1) |
|
és a dir, la suma dels 2 rectangles superiors obtinguts en partir l’interval [x1,x2] és menor que el rectangle superior definit per l’únic interval [x1,x2]. Anàlogament, podeu veure que la suma dels rectangles inferiors obtinguts partint l’interval [x1,x2] serà més gran que el rectangle inferior corresponent l’únic interval [x1,x2]. Tot això ens fa pensar que “si s’augmentés indefinidament el nombre de faixes de forma que les seves amplades tendissin a 0, llavors probablement les sumes Sn i sn tendirien a un mateix valor S”. Doncs, bé, quan això succeeix(*) es diu que el trapezi mixtilini corresponent té àrea definida, i que el valor de la seva àrea és S. Així doncs,
on se suposa que les sumes Sn i sn es formen de manera que les longituds dels intervals que fan de base tendeixen a 0. De fet, si forméssim Sn i sn agafant qualsevol successió de sumes, Sn , però prement com a altures les ordenades en punts intermitjos qualssevol, cn , tindríem
Així doncs, també es pot definir l’àrea d’un trapezi mixtilini mitjançant l’única fórmula següent: |
|
|
|
Definició d’integral d’una funció en un interval tancat [a,b ] |
|
El símbol La veritat és que el concepte d’integral definida està completament associat al càlcul d’àrees. Així es posa de manifest en les següent figures i en l’escena del final. |
|
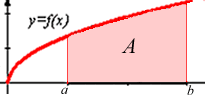
1. Si f és
una funció positiva en [a,b], llavors
|
|
|
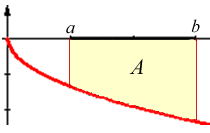
2. Si f és
una funció negativa en [a,b], llavors
|
|
|
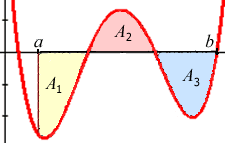
3. Si f
prem valors positius i negatius en [a,b], llavors |
|
|
càlcul aproximat d’integrals definides |
|
Per calcular una integral de forma aproximada, es poden aplicar els mateixos mètodes explicats per al càlcul d’àrees en els primers apartats: La regla del punt mig i la regla dels trapezis. Tanmateix, valen les mateixes fórmules d’error que es van exposar. Concretament, |
|
1. Regla del punt mig |
· M és una cota de la derivada segona de la funció |f | en l’interval [a,b]. · Si f és una funció parabòlica, f (x) = Ax2+Bx+C, aleshores M=2·|A| |
|
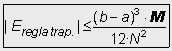
2. Regla dels trapezis |
· M és una cota de la derivada segona de la funció |f | en l’interval [a,b]. · Si f és una funció parabòlica, f (x) = Ax2+Bx+C, aleshores M=2·|A| |
|
Exercicis proposats |
|
1 |
Raoneu que l’àrea d’un paral·lelogram és igual al producte de la base per l’altura, és a dir, Àrea = b·h |
|
|
2 |
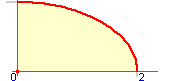
Dividint l'interval [0,2] en 3 parts iguals i aplicant després la fórmula de la regla dels trapezis, calculeu un valor aproximat de l'àrea del quadrant d'el·lipse representat en la figura. Només necessiteu saber que La funció que delimita la corba és
|
|
|
3 |
Dividint l'interval [0,2] en 5 parts iguals i aplicant després la fórmula de la regla del punt mig, calculeu un valor aproximat de l'àrea del quadrant d'el·lipse representat en la figura de l'exercici anterior |
|
4 |
Considereu l'àrea del recinte indicat en la figura adjunta, el costat corb de la qual correspon a la gràfica de la funció següent:
Esbrineu en quantes parts s'hauria de dividir l'interval [1, 4'5] per tenir la seguretat que en aplicar la regla del punt mig ens sortiria l'àrea amb error menor que 5 centèssimes. Després, feu la taula de càlculs corresponent per tal d'obtenir el valor aproximat de l'àrea. |
|
| 5 |
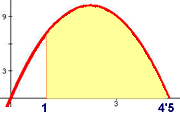
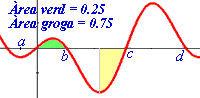
Calcula raonadament el valor de les integrals següents:
on f indica la funció representada en la figura adjunta a la dreta, i a, b, c, d indiquen els punts blaus, o sigui, els punts on la gràfica talla l'eix X. |
|
|
6 |
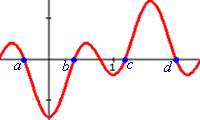
Amb les dades de la figura adjunta, calcula aproximacions raonables de les integrals següents:
on f indica la funció representada en la figura adjunta a la dreta. |
|
|
7 |
a) Utilitzant la fórmula de la regla del punt mig amb N=3, calculeu
b) En quantes parts com a mínim hauríem de dividir l'interval [0,3] per estar segurs que no cometríem un error superior a 0,01, si apliquéssim la regla del punt mig? c) Fes un dibuix indicant clarament què representa el valor de la integral anterior. |
|
8 |
Resoleu l'exercici anterior utilitzant la regla dels trapezis. |
|
|
(*) Malgrat que totes les presentacions gràfiques les farem amb funcions contínues, les definicions valdrán igualment per a funcions acotades no contínues,
(*) Es pot demostrar que el valor límit, S, no depèn de la forma en què es divideixin els intervals, i es pot demostrar també que això ocurrirà així amb qualsevol funció contínua, f.

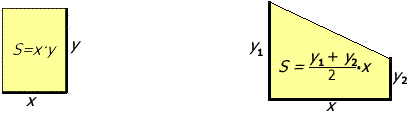
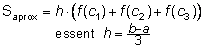
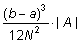 , o sigui, es compleix la fórmula
següent:
, o sigui, es compleix la fórmula
següent:
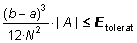 , de
la qual resulta
, de
la qual resulta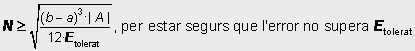
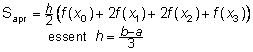

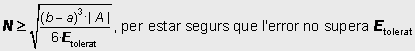
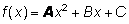 , l’error que ens pot produir la
fórmula anterior compleix:
, l’error que ens pot produir la
fórmula anterior compleix: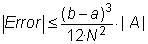

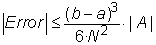

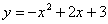 al llarg de l’interval
[0,3]. Dividint aquest interval en 3 parts iguals, calcula
una aproximació de l’àrea mitjançant la regla del punt mig, i altra
mitjançant la regla dels trapezis.
al llarg de l’interval
[0,3]. Dividint aquest interval en 3 parts iguals, calcula
una aproximació de l’àrea mitjançant la regla del punt mig, i altra
mitjançant la regla dels trapezis.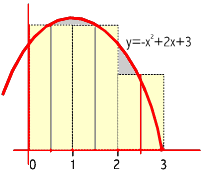
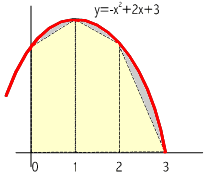

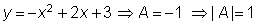
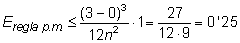
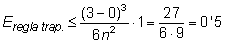
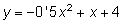 és
positiva en l’interval [1,3].
és
positiva en l’interval [1,3]. 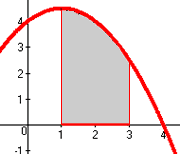
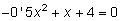 són –2
i 4. Per tant, com amb qualsevol paràbola, entre elles té signe
constant; també el tindrà, doncs, entre 1 i 3. El signe serà, per
exemple, el de y(0), el qual és evidentment positiu (y(0)=4)
són –2
i 4. Per tant, com amb qualsevol paràbola, entre elles té signe
constant; també el tindrà, doncs, entre 1 i 3. El signe serà, per
exemple, el de y(0), el qual és evidentment positiu (y(0)=4)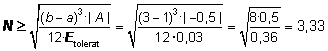


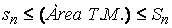 (1)
(1)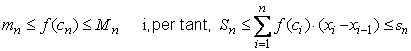

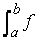 es llegeix integral
definida de la funció
es llegeix integral
definida de la funció 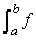 coincideix
amb l’àrea del seu trapezi mixtilini.
coincideix
amb l’àrea del seu trapezi mixtilini.