A la pràctica següent fareu servir l'aplicació Trapezi per calcular la integral d'una funció en un interval mitjançant el mètode dels trapezis.
 

La integral definida d'una funció f(x) en un interval [a,b], , és l'àrea compresa en la regió limitada per la gràfica de la funció, l'eix X i les rectes x = a y x = b. 

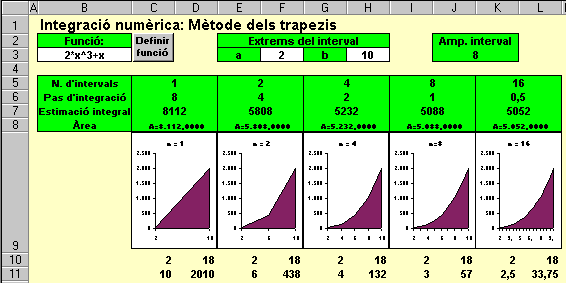
El mètode dels trapezis permet calcular de forma aproximada el valor de la integral definida. L'interval [a,b] es divideix en subintervals (4 a la figura) i la integral s'aproxima en cada subinterval per la superfície del trapezi dibuixat. 

Quan més gran és el nombre de subintervals en què es subdivideix l'interval inicial, millor és l'aproximació obtinguda. Aquest fet és destacat al full de càlcul Trapezi, on es calcula el valor aproximat dividint l'interval inicial en 2, 4, 8 o 16 subintervals. 
 

• Recupereu el fitxer MODUL7B1.XLS. 
• Seleccioneu el full Trapezi. 
• Entreu la funció y=2*x^3+x si és que no hi és. Premeu el botó Definir funció. 
• Modifiqueu l'interval d'integració i fixeu l'interval [2,10] modificant el valor de les cel·les F3 i H3. 
• Interpreteu el contingut dels 5 gràfics: 
• El primer gràfic correspon a un únic interval. La base del trapezi serà de 8 unitats. El valor estimat de la integral és de 8.112. 
• En el segon gràfic l'interval s'ha subdividit en dos intervals de 4 unitats d'amplada. El valor estimat és de 5.808. 
• ..... 
• En el cinquè gràfic l'interval s'ha subdividit en 16 intervals de 0,5 unitats d'amplada. El valor estimat és de 5.052. 
• Contrasteu amb el valor exacte de la integral definida en aquest cas que és 5.040. 
• Modifiqueu l'interval d'integració a [0,4], observeu els resultats obtinguts amb les diferents aproximacions i contrasteu amb el valor exacte, 136. 
• Calculeu de forma aproximada el valor de  utilitzant el full de càlcul. 

Haureu de: 
Modificar els límits d'integració de les cel·les F3 i H3. 
Modificar el rètol de la cel·la B3. 
Prémer el botó Definir funció. 
Repetir el procés amb la funció . 

Els comentaris de la primera pràctica, sobre protecció de dades i ocultació de fórmules, són també aplicables a aquest full. 

Les cel·les F3 i H3 contenen els intervals d'integració. 

La cel·la B3 inclou el rètol de la funció i el rang L10:L26 inclou la definició de la funció i la seva avaluació per a tots els valors que intervenen en els càlculs aproximats de la integral. 

Els rangs D10:D11, F10:F12, H10:H14 i J10:J18 prenen els seus valors del rang L10:L26. 

El rang C5:L5 incorpora el nombre d'intervals; el rang C6:L6 incorpora el pas d'integració (base dels rectangles); la regió C7:L7 inclou el càlcul aproximat de la integral mitjançant la fórmula del trapezi; la regió C8:L8 calcula els rètols pels gràfics. 

Cinc petites finestres permeten visualitzar gràficament la regió del pla corresponent als valors aproximats de la integral. 

Una macro associada al botó Definir funció permet copiar la funció definida a la cel·la B3 sobre la regió L10:L26.