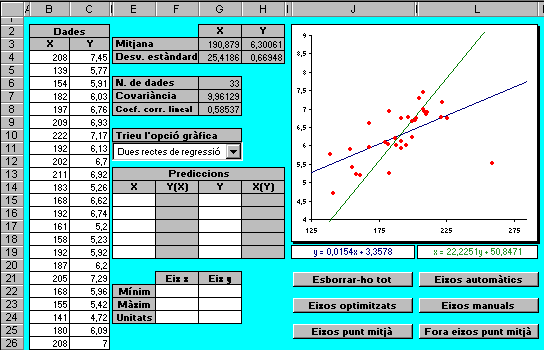
En totes les pràctiques de correlació i regressió que trobareu a continuació fareu servir el full anomenat Correlació i regressió del llibre MODUL7B2.xls, el funcionament del qual anireu aprenent a les mateixes pràctiques. 
 

Aquesta aplicació és un full de càlcul  que pot ser útil per analitzar la correlació lineal entre dues variables i, fins i tot, per trobar les rectes de regressió. Les dades que vulgueu analitzar s'han de situar a la regió B4:C203. Permet, per tant, estudiar fins a 200 parells de dades. Aquestes dades es poden introduir directament a les cel·les corresponents o bé copiar-les, totes de cop, des d'una base de dades o des d'un altre full de càlcul. 

Com està construït el full

El full està protegit contra escriptura de manera que només es poden modificar els valors de les cel·les amb fons blanc i el gràfic. Per poder veure els resultats de totes les fórmules del full haureu de desprotegir-lo i escollir la tinta de color negre, com ja s'ha explicat en pràctiques anteriors. 

A les cel·les N1, O1, N2 i O2 es calculen els coeficients a, b, c i d, respectivament, de les rectes de regressió. El rang N2:P13 conté els valors necessaris per dibuixar les dues rectes de regressió. En el rang N14:O17 es calculen l'origen i el final dels eixos, per tal d'optimitzar la visió del gràfic. Aquesta optimització s'aconsegueix amb una macro que s'executa amb el botó  Eixos optimitzats. En el rang F22:G24 es poden introduir uns valors per modificar l'escala dels dos eixos. La macro que fa això possible s'executa amb el botó Eixos manuals. Per tornar a l'escala per defecte cal prémer el botó Eixos automàtics i per esborrar totes les cel·les de fons blanc, el botó Esborrar-ho tot. Els botons Eixos punt mitjà i Fora eixos punt mitjà serveixen per incloure o retirar, respectivament, en el gràfic uns altres eixos, l'origen dels quals és el punt mitjà, és a dir, el format per les mitjanes de cada variable. En el rang E11:G11 hi hem col·locat una finestra desplegable per triar si el gràfic ha de representar només els punts, una o altra recta de regressió o, fins i tot, la superposició de les dues. Els rangs E15:E19 i G15:G19 serveixen per fer prediccions amb les rectes de regressió calculades. A la resta de cel·les amb fórmules es fan els càlculs indicats pels rètols corresponents. 

El gràfic és del tipus XY(Dispersión) i està fet per representar simultàniament els punts, les rectes de regressió i les prediccions fetes en el rang E15:H19. Per representar aquestes prediccions fem servir les barres d'error verticals i horitzontals. 
 

Correlació 1

L'objectiu d'aquesta pràctica és estudiar les possibles correlacions lineals existents entre unes variables obtingudes a partir d'unes proves d'Educació Física fetes per nois d'ESO. 

nnn

• Premeu el botó Esborrar-ho tot del full Correlació i regressió per començar la pràctica. Accediu al full EF del mateix llibre. Aquest  conté les variables amb què treballareu. Cada fila representa els resultats obtinguts per un alumne determinat en cada prova. Analitzem les variables: 
• ABDOM: conté el nombre de flexions abdominals que ha realitzat cada alumne en un temps determinat. 
• POTCA: representa els centímetres de llargada que ha saltat cada noi sense donar-se impuls i amb els peus junts. Ens dóna una mesura de la potència de cames. 
• TEMPS: indica el temps, en segons, obtingut per cada individu, en recórrer una distància de 60 metres llisos. 
• VELOM: expressa en metres/segon la velocitat mitjana de cada participant, calculada a partir de les dades de la variable TEMPS. 

• Comenceu a estudiar les variables POTCA i VELOM. Esbrineu quina relació hi ha entre la potència de cames i la velocitat mitjana en una prova de 60 metres. 
• Assegureu-vos que la regió d'entrada de dades (B4:C203) del full Correlació i regressió és buida (botó Esborrar-ho tot). 

Seleccioneu les dades de les variables POTCA i VELOM del full EF i copieu-les a partir de la cel·la B4 del full Correlació i regressió fent servir l'opció Pegado especial | Valores . 
A la cel·la G6 haurà sortit el nombre total de dades (33). També apareixen els valors dels paràmetres estadístics desitjats. 
• Trieu en la finestra desplegable del rang E11:G11 l'opció gràfica que vulgueu: 
• L'opció Només el núvol de punts, com el seu nom indica, només analitza la correlació lineal, sense buscar cap recta de regressió i permet veure el núvol de punts. 
• Les opcions y=ax+b i x=cy+d permeten buscar i representar gràficament les rectes de regressió de y sobre x i de x sobre y, respectivament. Les expressions d'aquestes rectes sortiran en les cel·les J19 i L19. 
• L'opció Dues rectes de regressió executarà simultàniament les opcions 2 i 3. 
• Premeu el botó Eixos optimitzats per tenir una visió del gràfic amb més detall. També podeu entrar valors al rang F22:G24  l'escala dels dos eixos i prémer el  botó Eixos manuals. 

• Feu clic a sobre el punt que heu de desplaçar diferents cops fins que el cursor es transformi en una creu amb les puntes en forma de fletxa. 
• Desplaceu el punt, amb el botó esquerre del ratolí premut, verticalment i/o horitzontalment i, en deixar anar el botó, observeu com varien els paràmetres calculats. 
• Feu clic a la finestra del gràfic i premeu el botó dret del ratolí. Trieu l'opció Opciones de gráfico del menú que ha sortit. 
• Entreu el títol i els rètols convenients i premeu Aceptar. 
• Si repetiu el procés amb POTCA i TEMPS, veureu com surt un valor del coeficient de correlació lineal proper a -1. 
• En canvi, si analitzeu les variables ABDOM i VELOM sortirà un valor de r proper a 0. 

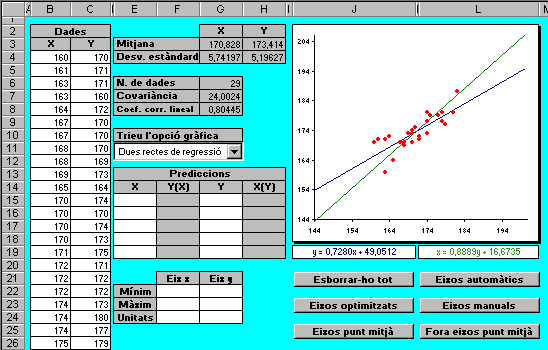
En aquesta pràctica s'insisteix en el concepte de regressió lineal, a partir de l'anàlisi de la relació entre les alçades d'uns pares i dels seus fills, i es treballa la possibilitat de fer prediccions a partir de les dues rectes de regressió. En un estudi similar, Francis Galton (1822-1911), a finals del segle passat, va utilitzar per primer cop el terme "regressió". 
 

• Premeu el botó Esborrar-ho tot del full Correlació i regressió. 
• Accediu al full Galton. Aquest  conté les alçades mitjanes, mesurades en cm, de 29 pares i les dels seus fills. 
• Copieu les dades del full Galton al rang d'introducció de dades del full Correlació i regressió com ho heu fet en la pràctica anterior. 
• Trieu l'opció gràfica Dues rectes de regressió de la finestra desplegable. 
• Premeu el botó Eixos optimitzats. 
• Fixeu-vos en les mitjanes i les desviacions estàndards. En mitjana, els fills són més alts que els pares i tenen una desviació estàndard molt similar. El coeficient de correlació lineal és bastant alt. 
• Apareixen els coeficients de les dues rectes de regressió. La primera (y = ax + b) servirà per fer prediccions des de l'alçada dels pares a la dels fills. L'altra recta (x = cy + d) serà útil per fer prediccions en sentit contrari. Observeu com les dues rectes es tallen en un punt que és precisament el punt mitjà del núvol de punts, és a dir, que té per coordenades les mitjanes de cada variable. 
• Situeu el cursor a la cel·la E15 per fer prediccions d'alçades dels fills a partir de les alçades dels pares, tot seguint la recta de regressió y = ax +b. 
• Ens preguntem quina alçada cal esperar que tinguin els fills d'uns pares de 155 cm o de 171 cm o de 190 cm. Per esbrinar-ho entreu a les cel·les E15, E16 i E17 les alçades 155, 171 i 190 cm respectivament. Observeu les alçades dels fills que surten a les cel·les F15, F16 i F17. En el gràfic podeu observar com s'han calculat aquestes prediccions. 

• Plantegem ara les prediccions en sentit contrari. Quina alçada cal esperar que tinguin els pares d'uns fills de 160, 175 i 190 cm? Per esbrinar-ho entreu aquestes dades a les cel·les G15, G16 i G17, respectivament. Les alçades buscades sortiran a les cel·les H15, H16 i H17. En el gràfic surten, amb un altre color, representades aquestes prediccions. 
• Feu més prediccions en ambdós sentits i traieu les vostres pròpies conclusions. 

En aquesta pràctica podeu analitzar tres exemples de núvols de punts en què, tot i que el seu aspecte gràfic és molt diferent, tenen aproximadament el mateix coeficient de correlació lineal (r = 0,816) .Utilitzeu els fulls A, B i C del mateix llibre.
 

• Analitzeu consecutivament la correlació lineal de les dades dels fulls A, B i C d'aquest mateix llibre. 
• Observeu que, tot i que tenen gràfics ben diferents, els coeficients de correlació lineal i les rectes de regressió són pràcticament iguals.