La darrera pràctica d'aquest mòdul tracta el tema de les inequacions. Veureu com introduir diverses inequacions amb una incògnita i la resposta de la Wiris. També hi ha una activitat per treballar gràficament les inequacions de primer grau amb dues incògnites.

Els símbols necessaris per definir i treballar amb equacions o inequacions es mostren en la taula següent. La Wiris té icones a la pestanya per escriure'ls; aquesta opció és la que dóna la millor qualitat tipogràfica, però també es poden entrar mitjançant el teclat o amb una combinació de tecles.

• La Wiris resol aquelles inequacions amb una variable que permetrien la resolució de l'equació associada amb la comanda resol.
• La sintaxi de la comanda és resol_inequació(expressió de la inequació).
• Es poden utilitzar variables o expressions definides anteriorment.
• La Wiris retorna la solució de les inequacions mitjançant els operadors lògics & i |. Si apareixen els dos operadors, s'entén que & té prioritat sobre |.
  
  
  
• Si l'equació no té solució, la resposta és fals.
• Si l'inequació té per solució qualsevol valor real de x, és a dir, si la desigualtat és certa per a qualsevol x, la resposta és cert.
• Els exemples de la finestra següent corresponen diverses inequacions polinòmiques.

• Canvieu la funció per alguna altra que no resolgui numèricament i observeu la resposta de la Wiris.
• Observeu la representació gràfica de la funció associada a la inequació.

• Les comandes d'escriptura fan coincidir el color del text amb l'interval corresponent.

• Observeu les dues opcions per introduir un sistema: en forma de llista o bé amb l'operador &.
• En el darrer sistema d'inequacions interpreteu els resultats.
• Plantegeu altres inequacions i sistemes.

L'activitat següent serveix per interpretar gràficament les solucions d'una inequació de primer grau amb dues incògnites.
Es representa una recta definida a partir de dos punts, se'n calcula l'equació implícita
Ax + By + C = 0, i es defineix la funció de dues variables f(x, y) = Ax + By + C.
Des del tauler gràfic, s'observa que els valors d'aquesta funció en els punts del mateix semiplà que defineix la recta són del mateix signe, i els de l'altre semiplà són tots de signe contrari. Per tant, els punts de cada semiplà representen gràficament una de les inequacions:
Ax + By + C < 0 o Ax + By + C > 0.

En la finestra activa observeu els diferents passos:

• La recta AB es defineix a partir de dos punts que es poden moure des del tauler gràfic.
• El punt C és un punt auxiliar que s'utilitza per saber el sentit de la desigualtat.
• La comanda equació(r) retorna l'equació de la recta en la forma y = ax + b, o bé
  x = a, si és el cas. Aquesta expressió és una llista. El primer element de la llista és l'expressió a l'esquerra de la igualtat, i el segon és l'expressió a la dreta.
• A partir d'aquestes dues expressions, es defineix la funció f(x, y) = y - ax - b, o bé
  f(x) = x - a.
• La comanda avalua dóna el valor de f(x, y) en el punt C. La icona pertany al menú i en aquest cas assigna un valor a les variables x i y.

La Wiris no inclou la resolució dels sistemes d'inequacions lineals amb diverses variables (és a dir, el que seria el dibuix de la regió factibe; si ens interessa ho hem de programar nosaltres com es veu més avall) però, en canvi, sí que aplica el mètode del símplex per a obtenir el valor màxim o mínim d'una funció lineal en la regió factible d'un sistema d'inequacions, el que es coneix com el problema fonamental de la programació lineal.

Les comandes que resolen aquesta qüestió (que no apreixen a la documentació del programa però que funcionen perfectament) són

• màxim_amb_restriccions
• mínim_amb_restriccions

a les quals s'han de passar com a arguments

• ( funció,{llista de les inequacions (que pot ser una llista vertical)})

i llavors la Wiris considera "automàticament" que a la llista d'inequacions donades cal afegir-hi les que resulten de considerar que totes les variables (que poden ser més de dues, les que interessin) han de prendre valors positius o zero.

Podeu veure'n ben bé la sintaxi en uns exemples .
Es tracta de buscar el màxim i el mínim que assoleix la funció 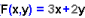en la regió definida per les inequacions 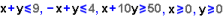i com ja hem dit la resposta ens la dóna automàticament la calculadora. Però a banda d'això hi veureu el codi perquè la Wiris mostri la regió factible i un punt mòbil, al costat del qual es veu el valor de la funció en aquest punt. Així podreu descobrir empíricament on s'assoleix el màxim o el mínim
(i veureu una altra aplicació de la construcció de llistes, que ja hem comentat que era un recurs molt important per treballar eficaçment amb la Wiris).

Encara que no tinguem una comanda específica per visualitzar de sistemes d'inequacions amb dues variables, sí que podem dibuixar-ne (aproximadament) el conjunt de solucions!