|
||||||||||||||||
| Pràctica |
|
|
|
Exercicis
|
||||||||||||
| Àlgebra lineal | |
|
En aquesta pràctica coneixereu els recursos que incorpora la calculadora
Wiris per al treball amb els elements bàsics de l'àlgebra
lineal: vectors i matrius. La carpeta que s'obre amb la pestanya |
|
 |
|
|
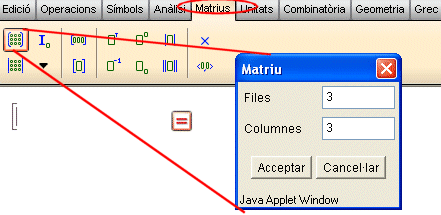
Icones per introduir vectors, matrius i determinants
i finestra emergent per modificar les dimensions d'una matriu |
|
|
Com a part central de la pràctica treballarem els sistemes d'equacions lineals i veurem la possibilitat d'enfocar-ne l'estudi des d'un punt de vista matricial. En particular s'explicarà la sintaxi adequada perquè, en cas d'indeterminació, s'expressin unes variables en funció d'unes altres que es prenen com a variables lliures i es repassaran les idees de llistes de taules com a estructura formal de les solucions que ens dóna la Wiris. |
|
|
|
Vectors |
Per crear un vector ho podem fer amb la icona Alternativament podem fer-ho:
La calculadora Wiris incorpora totes les operacions habituals amb vectors, que s'aplicaran sempre que es compleixin les condicions perquè l'operació es pugui fer.
Per als espais vectorials reals tenim també la possibilitat de
calcular la norma d'un vector, amb la comanda norma
o la icona A la finestra activa següent trobareu exemples d'aquests recursos que acabem de comentar i, a més, de l'aplicació de diversos booleans, entre ells linealment_independents? que «sap reconèixer» si treballem amb un espai vectorial sobre el cos del nombres reals o bé sobre el cos dels nombres complexos (si hi ha algun element on aparegui un d'aquests nombres). Observeu i experimenteu noves possibilitats! |
|
 |
|
|
La calculadora Wiris no incorpora la resolució directa d'equacions vectorials. Per aquesta raó si volem resoldre el problema d'escriure un vector com a combinació lineal d'altres (en particular si volem trobar els components d'un vector en una base) caldrà que construïm les equacions numèriques equivalents a l'equació vectorial.
Hem vist anteriorment l'exemple de tres vectors linealment dependents. En la finestra activa següent podeu estudiar, entre altres coses, com es pot obtenir la combinació lineal que dóna el tercer vector en funció dels altres dos. |
|
 |
|
| Podeu consultar una finestra d'ampliació on es resol sistemàticament el problema de trobar el rang d'un conjunt de vectors i es fa la selecció dels que són independents. Si us interessa el tema, us suggerim que l'analitzeu després d'estudiar el proper apartat i heu de saber que es fa servir un recurs de combinatòria (tema que s'estudia amb detall a la pràctica 1 del darrer mòdul del curs.) | |
|
|
Matrius |
Aquesta idea dóna la primera manera d'introduir una matriu, com
un vector de vectors; fixeu-vos que ha de ser un vector, no una llista.
Tanmateix, preferiblement podem fer-ho amb la icona La imatge següent mostra dues maneres d'entrar matrius de dues files i quatre columnes i una primera operació entre elles.
Per fer operacions amb matrius i altres càlculs les instruccions són aquestes:
Per tal d'emprar elements definidors d'una matriu en altres càlculs tenim les opcions següents:
Per obtenir el determinant d'una matriu quadrada hi ha dues possibilitats:
Disposem també de la comanda rang(M) que, com és natural, ens dóna el rang de la matriu. Obriu la finestra activa que correspon a la icona següent i podreu practicar molts d'aquests recursos, a més dels que ja veieu a la imatge. Convé que us adoneu que, a l'hora d'operar una matriu i un vector, encara que el vector estigui escrit horitzontalment, la Wiris l'interpreta com a vector vertical si això és el que escau. |
|
 |
|
|
A part d'aconsellar-vos, com sempre, que investigueu altres possibilitats pel vostre compte, us suggerim algunes variacions sobre els exemples que teniu a la finestra activa:
...i si ho feu, penseu a guardar la feina, perquè us pot servir per als exercicis. |
|
|
|
Sistemes d'equacions lineals |
|
Al final de la pràctica 3 del mòdul 1 hem vist com introduir les comandes per resoldre un sistema en forma d'equacions. La pràctica anterior ha estat destinada a l'estudi dels sistemes d'equacions però ha semblat interessant fer un tractament més aprofundit dels sistemes d'equacions lineals en el conext de les tècniques de l'àlgebra lineal. Començarem observant el comportament de la Wiris amb cada un dels tres tipus de sistemes possibles, segons el nombre de solucions, i en un altre apartat ho confrontarem amb la presentació matricial. |
|
|
|
Podeu obrir una finestra activa fent clic a la icona de l'esquerra. Llavors, a part de fer les vostres pròpies proves i assajos, convé que completeu els exemples que hi trobareu seguint les instruccions que es detallen tot seguit. |
 |
|
|
Recordeu el signe d'igual llarg per les equacions |
|
|
|
|
En els exàmens que es proposen a les noies i els nois del batxillerat són «clàssics» els problemes que demanen que s'estudiï un sistema d'equacions segons el valor que prenen alguns paràmetres que hi apareixen. En realitat, doncs, no estem estudiant un sistema d'equacions sinó una família de sistemes d'equacions. Tot seguit analitzem un exemple i fem una primera passada pel tema, que serà completat mitjançant la visió matricial dels sistemes lineals.
|
|
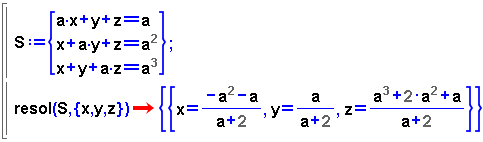 |
|
|
Ara es tracta d'analitzar en quins casos aquesta solució no és vàlida.
Sembla que ha de ser possible sistematitzar aquest estudi. És ben cert i ho farem amb els recursos que s'estudien a l'apartat següent. |
|
|
|
Punt de vista matricial dels sistemes d'equacions lineals |
|
Un sistema d'equacions lineals es pot escriure en forma matricial: com A·XT=BT on A és la matriu del sistema, X és el vector de les incògnites i B és el vector de termes independents. La comanda resol de la calculadora Wiris admet com a arguments la matriu d'un sistema d'equacions lineals i el vector de termes independents i, com podeu observar si obriu la finestra activa següent:
|
|
 |
|
| El teorema de Rouché-Frobënius comporta la classificació d'un sistema d'equacions lineals a partir del plantejament matricial. Si us interessa el tema, combinat amb l'aprofundiment d'aspectes del llenguatge de programació Wiris++, cliqueu a la icona d'ampliació. | |
|
En acabar l'apartat anterior dèiem que amb nous recursos seria possible sistematitzar l'estudi dels sistemes amb paràmetres. És clar que el recurs fonamental és el càlcul del determinant de la matriu del sistema. En la finestra activa següent podeu veure una manera de fer-ho; en primer lloc es resol el sistema per al cas general. Tot seguit es calcula el determinant i, igualant-lo a 0, això permet conèixer tots els casos especials d'indeterminació o incompatibilitat i afegir les línies adequades per estudiar el sistema en aquests casos. També podreu analitzar un segon tipus d'exemple més difícil de sistematitzar: un sistema de més equacions que incògnites. |
|
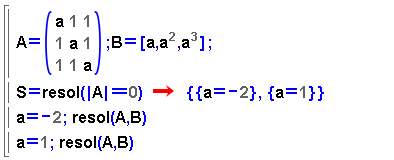 |
|
| Si us interessa la programació amb Wiris++ teniu una nova finestra d'ampliació que permet la classificació dels sistemes de tres equacions amb tres incògnites i un paràmetre a. | |