|
|
En aquesta pràctica veureu els mètodes de creació
dels sòlids primitius de la barra d'eines Sólidos
de l'AutoCAD 2002.
|
| |
|
|
|
Sòlids primitius |
|
|
|
|
|
La creació directa de sòlids |
| |
|
|
|
L'AutoCAD 2002 ofereix diverses possibilitats
per crear objectes tridimensionals dins de l'entorn espacial del programa.
La més senzilla, i que veureu en aquesta pràctica, és
la creació directa d'objectes tridimensionals mitjançant
les eines incloses a la barra d'eines Sólidos:
Prisma rectangular, Esfera,
Cilindro, Cono,
Cuña i Toroide.
Aquests objectes tridimensionals de creació directa s'anomenen
sòlids primitius.
La barra d'eines Sólidos inclou
altres eines que, a diferència de les anteriorment esmentades,
ens permeten crear objectes sòlids a partir de plans prèviament
dibuixats; veureu el funcionament d'aquestes eines més endavant.
|
| |
|
| |
Figura 1. Barra d'eines Sólidos. Els sis
primers botons corresponen als sòlids de creació directa:
Prisma rectangular, Esfera, Cilindro, Cono, Cuña i Toroide
|
| |
|
|
|
A continuació, veureu els
mètodes de creació dels sòlids de creació directa.
Per veure millor els resultats, obriu un document nou de les mesures que
us dóna per defecte l'assistent de configuració ràpida,
visualitzeu l'espai de dibuix des de la vista isomètrica SO
i activeu la Rejilla amb els seus paràmetres
per defecte. |
| |
|
|
|
Prisma rectangular |
| |
|
|
|
El Prisma rectangular és el primer
dels objectes sòlids que podeu crear mitjançant les eines
que us mostra la barra d'eines Sólidos.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Prisma rectangular
 de la barra d'eines Sólidos. de la barra d'eines Sólidos.
- Menú Dibujo|Sólidos|Prisma
rectangular.
- Escrivint prismarect a la barra de
comandament i prement la tecla de Retorn.
Podeu fer un prisma rectangular mitjançant tres mètodes:
- Definint la primera cantonada i la cantonada oposada de la base del
prisma, i finalment l'alçada d'aquest.
- Definint les mesures de les seves arestes.
- Definint el centre del prisma i a continuació la mesura de
les seves arestes.
|
|
|
Prisma rectangular definit a partir
de la base |
| |
|
|
|
- Escriviu prismarect a la barra de
comandaments i premeu la tecla de Retorn.
El programa us demanarà el següent: Precise
esquina de prisma o [Centro] <0,0,0>:; premeu directament
la tecla de Retorn per acceptar les
opcions per defecte que se us donen.
- A Precise esquina o [Cubo/Longitud]: definiu
la cantonada següent de la base del prisma; escriviu @70,50
i premeu la tecla de Retorn. D'aquesta
manera, el prisma tindrà una base de 70 unitats de dibuix sobre
l'eix X i 50 unitats de dibuix sobre l'eix Y.
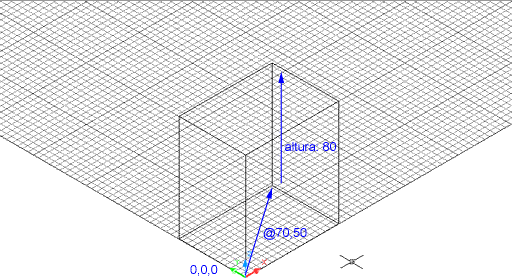
- L'última pregunta és Precise altura:.
Definiu l'alçada del prisma -la seva mesura sobre l'eix Z-
introduint un valor, per exemple 80,
i prement la tecla de Retorn.
Un cop acabada la realització del prisma, i només per veure
millor el resultat obtingut, visualitzeu la figura com a estructura lineal
3D amb el menú Ver|Sombra|Estructura
alámbrica 3D.
|
| |
|
| |
|
| |
Figura 2. Prisma rectangular de base 70 x 50 unitats
de dibuix (X, Y) i alçada 80 unitats de dibuix
|
| |
|
|
|
Prisma rectangular definit per
les seves arestes |
| |
|
|
|
Esborreu el prisma anterior, tot seleccionant-lo normalment i prement
la tecla de Supressió -Supr-;
ara comprovareu el mètode de creació de prismes a partir
de la definició de les seves arestes.
- Escriviu prismarect a la barra de
comandaments i premeu la tecla de Retorn.
A la pregunta Precise esquina de prisma o [Centro]
<0,0,0>:, premeu directament la tecla de Retorn
per acceptar les opcions per defecte que se us donen.
- A la següent pregunta de la barra de comandaments, Precise
esquina o [Cubo/Longitud]:, responeu tot teclejant
la lletra L i
prement la tecla de Retorn.
- Ara el programa us demana Precise longitud:.
Introduïu un valor per a la mesura de les arestes del prisma paral·leles
a X, per exemple, 90 i premeu
la tecla de Retorn.
- El paràmetre següent que us demana és la mesura
de les arestes paral·leles a Y: Precise
anchura: Introduïu un valor, per exemple, 45
i premeu la tecla de Retorn.
- L'última pregunta és Precise altura:
per indicar la mesura de les arestes paral·leles a leix Z. Introduïu
un valor, per exemple 80, i premeu
la tecla de Retorn.
|
| |
|
| |
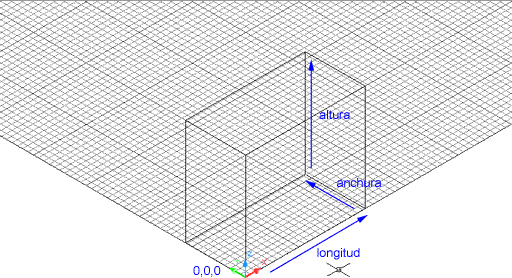
Figura 3. Prisma rectangular definit a partir de la
mesura de les seves arestes: para.leles a X , a Y i a Z
|
| |
|
|
|
L'ordre Prisma
rectangular també permet crear un prisma a partir del centre
i després definir la mesura de les seves arestes, de manera idèntica
a l'anteriorment descrita, així com també permet crear un
cub, donant únicament l'origen del mateix o el seu centre i una única
mesura per les seves arestes. |
| |
|
|
|
Esfera |
| |
|
|
|
L'Esfera és el segon sòlid
que podeu crear mitjançant les eines que us mostra la barra d'eines
Sólidos.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Esfera
 de la barra d'eines Sólidos.
de la barra d'eines Sólidos.
- Menú Dibujo|Sólidos|Esfera.
- Escrivint esfera a la barra de comandament
i prement la tecla de Retorn.
Podeu fer una esfera mitjançant dos mètodes:
- Definint el centre de l'esfera i el seu radi.
- Definint el centre de l'esfera i el seu diàmetre.
|
| |
|
|
|
- Escriviu esfera a la barra de comandaments
i premeu la tecla de Retorn.
- La primera pregunta que el programa us fa és Precise
centro de la esfera <0,0,0>:. Per veure millor el resultat,
entreu la coordenada 50,50,50 i premeu
la tecla de Retorn.
- A continuació, el programa us demana Precise
radio de la esfera o [Diámetro]:. Ja que heu ubicat el
centre de l'esfera a 50 unitats de dibuix per sobre de l'origen de coordenades,
introduïu un radi de 50 i premeu
la tecla de Retorn.
Si teclegeu la lletra d
i premeu la tecla de Retorn,
el valor que posteriorment introduïu serà el del diàmetre
de l'esfera.
L'estructura de filferro resultant resulta molt difícil de veure
com una esfera; per aquest motiu, canvieu el tipus d'ombrejat a Sombreado
Gouraud.
|
| |
|
| |
|
| |
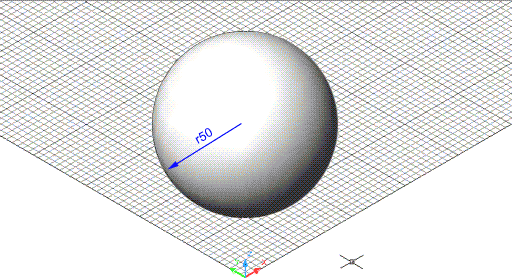
Figura 4. Esfera definida a partir del centre i el radi,
visualitzada amb un ombrejat Gouraud
|
| |
|
| |
Cilindre |
| |
|
|
|
El Cilindro és el tercer sòlid
que podeu crear mitjançant les eines de la barra d'eines Sólidos.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Cilindro
 de la barra d'eines
Sólidos. de la barra d'eines
Sólidos.
- Menú Dibujo|Sólidos|Cilindro.
- Escrivint cilindro a la barra de
comandament i prement la tecla de Retorn.
Podeu fer dos tipus diferents de cilindres:
- Cilindres amb base circular.
- Cilindres amb base el·líptica.
El mètode per crear tant els uns com els altres és bàsicament
idèntic:
- Definir el centre i el radi o diàmetre de la base en el cas
dels cilindres amb base circular, i després l'alçada dels
mateixos.
- Definir els eixos major i menor de l'el·lipse que serveix de
base als cilindres de base el·líptica, i després
l'alçada.
|
|
|
Cilindre de base circular |
| |
|
|
|
- Esborreu l'objecte anteriorment realitzat, i escriviu cilindro
a la barra de comandaments i premeu la tecla de Retorn.
- La primera pregunta que el programa us fa és Precise
centro de base de cilíndro o [Elíptico] <0,0,0>:.
Determineu la coordenada 50,50,0 i
premeu la tecla de Retorn.
- A continuació, el programa us demana Precise
radio de base de cilíndro o [Diámetro]:. Introduïu
un radi de 30 i premeu la tecla de
Retorn. Si teclegeu
la lletra d
i premeu la tecla de Retorn,
el valor que posteriorment introduïu serà el del diàmetre
de la circumferència de la base del cilindre.
- La pregunta següent és Precise altura
del cilindro o [Centro del otro extremo]: ; introduïu un
valor per l'alçada, per exemple 60,
i premeu la tecla de Retorn.
Observeu el resultat amb un ombrejat Gouraud.
|
| |
|
| |
|
| |
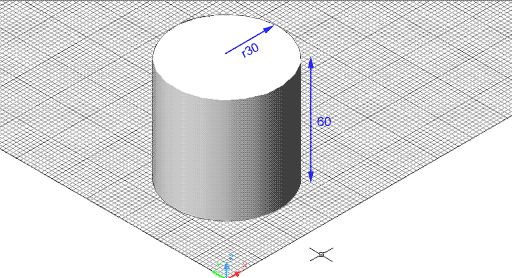
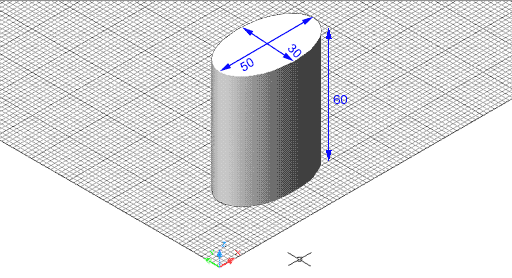
Figura 5. Cilindre de base circular visualitzat amb
un ombrejat Gouraud
|
| |
|
|
|
Cilindre de base el·líptica |
| |
|
|
|
- Esborreu el cilindre anteriorment realitzat, escriviu de
nou cilindro a la barra de comandaments
i premeu la tecla de Retorn.
- A la pregunta Precise centro de base de cilíndro
o [Elíptico] <0,0,0>: responeu teclejant la lletra
e i prement la tecla de Retorn.
- A continuació, el programa us demana Precise
punto final de eje de el.lipse para base de cilíndro o [Centro]:
Com succeïa amb l'ordre el·lipse, heu de determinar
o bé els eixos de l'el·lipse o bé un centre, i
després mig eix major i mig eix menor. Determineu com a punt
final d'un eix la coordenada 30,30,0
i premeu la tecla de Retorn.
- La pregunta següent és Precise punto
final de segundo eje de el.lipse para base de cilíndro:
Tot i que la pregunta està plantejada de manera poc clara, el
que heu d'introduir aquí és la coordenada que determini
l'extrem de l'eix que heu començat a definir amb la coordenada
anterior. Introduïu una coordenada, per exemple @50,0,
per determinar un eix de l'el·lipse que mesuri 50 unitats de
dibuix, i premeu la tecla de Retorn.
- La pregunta següent, també mal plantejada, és Precise
longitud de otro eje para base de cilindro: Aquí NO heu
d'introduir la longitud total de l'esmentat segon eix, sinó la
meitat de la seva longitud, ja que el programa l'està calculant
des del centre del primer eix. Suposem que la base del cilindre que
esteu fent ha de ser una el·lipse amb un eix major de 50 unitats
de dibuix -ja definit en els passos anteriors- i un eix menor de 30;
doncs bé, de ser així, el valor que ara heu d'introduir
és 15, i prémer la tecla
de Retorn.
- L'última pregunta és Precise altura
del cilindro o [Centro del otro extremo]:; introduïu un valor
per l'alçada, per exemple 60,
i premeu la tecla de Retorn.
Observeu el resultat amb un ombrejat Gouraud.
|
| |
|
| |
|
| |
Figura 6. Cilindre de base el·líptica
visualitzat amb un ombrejat Gouraud
|
| |
|
|
|
Per evitar els malentesos esmentats en el punt anterior, podeu fer servir
el mètode centre/longitud dels eixos a l'hora de fer un cilindre
de base el·líptica. Només haureu de considerar que
les mides que s'han de donar han de ser la meitat de la mida total de
cadascun dels eixos.
Per fer un cilindre com el de la figura 6 amb aquest mètode, en
primer lloc indicaríeu el centre de l'el·lipse base, coordenada
@45,30,0 i a continuació la meitat
de la mesura total dels eixos: @25,0
per a l'eix major i @0,15 per a l'eix
menor. Després, com en el cas anterior, determinaríeu l'alçada
del prisma, 60 unitats de dibuix.
|
| |
|
|
|
Con |
| |
|
|
|
El Cono és la quarta figura sòlida
que trobeu a la barra d'eines Sólidos.
Com en el cas del Cilindro, també
hi ha cons de base circular i cons de base el·líptica. Els
mètodes de creació són, òbviament, molt similars.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Cono
 de la barra d'eines Sólidos.
de la barra d'eines Sólidos.
- Menú Dibujo|Sólidos|Cono.
- Escrivint cono a la barra de comandament
i prement la tecla de Retorn.
Podeu fer dos tipus diferents de cons:
- Cons amb base circular.
- Cons amb base el·líptica.
El mètode per crear tant els uns com els altres és:
- Definir el centre i el radi o diàmetre de la base en el cas
dels cons amb base circular, i després l'alçada.
- Definir els eixos major i menor de l'el·lipse que serveix de
base als cons de base el·líptica, i després l'alçada.
|
|
|
Con de base circular |
| |
|
|
|
- Esborreu el cilindre anteriorment realitzat, escriviu cono
a la barra de comandaments i premeu la tecla de Retorn.
- La primera pregunta que el programa us fa és Precise
centro de base de cono o [Elíptico] <0,0,0>: Determineu
la coordenada 50,50,0 i premeu la tecla
de Retorn.
- A continuació, el programa us demana Precise
radio de base de cono o [Diámetro]:. Introduïu un
radi de 30 i premeu la tecla de Retorn.
Si teclegeu la lletra d
i premeu la tecla de Retorn,
el valor que posteriorment introduïu serà, com en el cas
del cilindre, el del diàmetre de la circumferència de
la base del con.
- La pregunta següent és Precise altura
de cono o [Vértice]:; introduïu un valor per a l'alçada,
per exemple 60, i premeu la tecla de
Retorn.
Observeu el resultat amb un ombrejat Gouraud.
|
| |
|
| |
|
| |
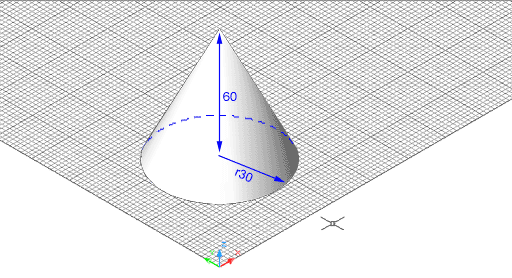
Figura 7. Con de base circular visualitzat amb un ombrejat
Gouraud
|
| |
|
| |
Con de base el·líptica |
| |
|
|
|
- Esborreu el con anteriorment realitzat, escriviu de
nou cono a la barra de comandaments
i premeu la tecla de Retorn.
- A la pregunta Precise centro de base de cono o
[Elíptico] <0,0,0>: responeu teclejant la lletra
e i prement la tecla de Retorn.
- A continuació, el programa us demana Precise
punto final de eje de el.lipse para base de cono o [Centro]:.
Com en al cas del cilindre, heu de determinar o bé els eixos
de l'el·lipse o bé un centre, i després mig eix
major i mig eix menor. Determineu com a punt final d'un eix la coordenada
30,30,0 i premeu
la tecla de Retorn.
- La pregunta següent és Precise punto
final de segundo eje de el.lipse para base de cono: Com en el
cas del cilindre, determineu el punt final del primer eix de l'el·lipse,
per exemple @50,0 , i premeu la tecla
de Retorn.
- La pregunta següent, també mal plantejada, és Precise
longitud de otro eje para base de cono: De nou, NO heu d'introduir
la longitud total de l'esmentat segon eix, sinó la meitat de
la seva longitud; introduïu un valor, per exemple 15,
i premeu la tecla de Retorn.
- L'última pregunta és Precise altura
de cono o [Vértice]:; introduïu un valor per a l'alçada,
per exemple 70, i premeu la tecla de
Retorn.
Observeu el resultat amb un ombrejat Gouraud.
|
| |
|
| |
|
| |
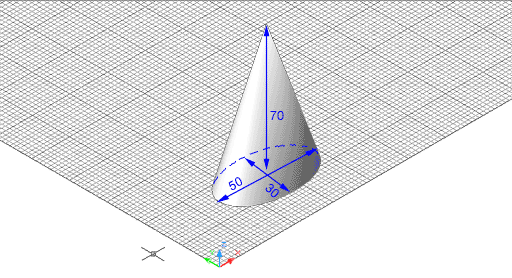
Figura 8. Con de base el·líptica visualitzat
amb un ombrejat Gouraud
|
| |
|
|
|
Naturalment, tot allò esmentat
respecte als cilindres de base el·líptica és aplicable
als cons de base el·líptica. Per tant, és també
pràctic en aquest cas fer servir el mètode centre/mesura dels
eixos. |
| |
|
|
|
Falca |
| |
|
|
|
L'anomenada Cuña
és la cinquena figura sòlida que trobeu a la barra d'eines
Sólidos, és en realitat
un prisma que té per bases triangles rectangles. Els seus mètodes
de creació són molt similars a aquells del Prisma
rectangular.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Cuña
 de la barra d'eines Sólidos. de la barra d'eines Sólidos.
- Menú Dibujo|Sólidos|Cuña.
- Escrivint cuña a la barra
de comandament i prement la tecla de Retorn.
Els mètodes per crear una cuña
són:
- Definir la primera cantonada i la cantonada oposada d'un costat del
prisma -que farà de base-, i l'alçada, que equival a la
mesura d'un segon costat.
- Definint les mesures dels costats.
- Definint el centre del prisma i a continuació la mesura de
les seves arestes.
|
| |
|
|
|
- Esborreu el con anteriorment realitzat, escriviu cuña
a la barra de comandaments i premeu la tecla de Retorn.
- La primera pregunta, Precise primera esquina de
cuña prisma o [Centro] <0,0,0>: us demana, com en
el cas del prisma rectangular, que definiu un origen per la figura;
indiqueu com a tal la coordenada 20,20,0
i premeu la tecla de Retorn.
- La pregunta següent, idèntica a la del prisma, us demana
Precise esquina o [Cubo/Longitud]: Definiu
la següent cantonada de la base de la cunya mitjançant coordenades:
esciviu @70,50 i premeu la tecla de
Retorn. D'aquesta manera, el costat
de la cunya que farà de base mesurarà 70 unitats de dibuix
sobre l'eix X i 50 unitats de dibuix sobre l'eix Y.
- L'última pregunta és Precise altura:
Definiu l'alçada, o el que és el mateix, la segona mesura
del costat de la cunya que quedarà perpendicular al pla de terra;
escriviu per exemple 80, i premeu la
tecla de Retorn.
Visualitzeu la figura com a estructura lineal 3D -menú Ver|Sombra|Estructura
alámbrica 3D.
|
| |
|
| |
|
| |
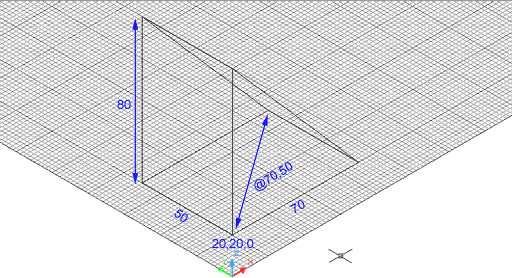
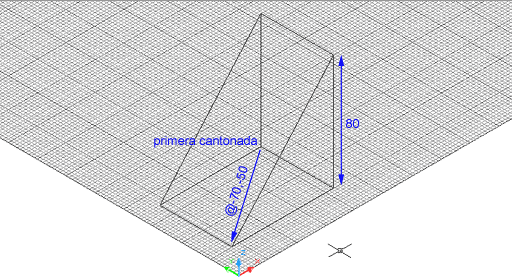
Figura 9. Falca de base 70 x 50 unitats de dibuix i
alçada 80 unitats de dibuix
|
| |
|
|
|
Si voleu que la falca tingui el pla inclinat cap a vosaltres, el que
heu de fer és senzillament definir el pla que fa de base d'esquerra
a dreta -és a dir, definint les X com a negatives.
Per exemple, una falca idèntica en mides a la de la figura 9 la
base de la qual hagués estat definida com a @-70,50
o @-70,-50, donaria com a resultat el
següent:
|
| |
|
| |
|
| |
Figura 10. Falca de base 70 x 50 unitats de dibuix i
alçada 80 unitats de dibuix, definida la seva base de esquerra
a dreta -X negatives
|
| |
|
|
|
Perquè el pendent de la falca
no fos en direcció X, caldria girar sobre l'eix Z la
icona SCP, de manera que l'eix X s'orientés cap allà
a on volguéssiu. |
| |
|
|
|
Toroide |
| |
|
|
|
L'última figura de la barra d'eines Sólidos
és el torus o toroide.
Podeu executar l'ordre de tres maneres:
- Fent clic al botó Toroide
 de la barra d'eines Sólidos. de la barra d'eines Sólidos.
- Menú Dibujo|Sólidos|Toroide.
- Escrivint toroide a la barra de comandament
i prement la tecla de Retorn.
|
| |
|
|
|
Per crear un toroide hi ha un únic mètode, amb dues possibilitats
a l'hora d'indicar els paràmetres al programa per realitzar-lo:
indicar radis o bé indicar diàmetres.
- Esborreu la cunya anteriorment realitzada,
escriviu toroide a la barra de comandaments
i premeu la tecla de Retorn.
- La primera pregunta, Precise centro de toroide
<0,0,0>: us demana que definiu un punt central per la figura;
indiqueu com a tal la coordenada 80,80,20
i premeu la tecla de Retorn.
- La pregunta següent, Precise radio de toroide
o [Diámetro]: us demana que indiqueu el radi o bé
el diàmetre de la figura, tenint en compte que aquest va des
del centre del toroide fins al centre de la secció de la figura.
Introduïu, a manera d'exemple, un radi de 50
unitats de dibuix -de manera que la figura "tocarà"
al pla de terra- i premeu la tecla de Retorn.
- L'última pregunta, Precise radio de sección
o [Diámetro]: us demana que indiqueu el radi o el diàmetre
de "gruix" de la figura; escriviu 20,
i premeu la tecla de Retorn.
El resultat és el següent:
|
| |
|
| |
|
| |
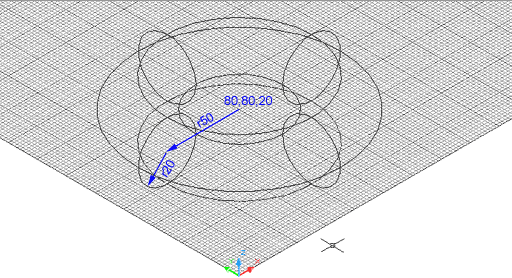
Figura 11. Toroide de radi 50 i secció 20 unitats
de dibuix, visualitzat amb estructura de filferro 3D
|
| |
|
|
|
Per entendre millor la figura, visualitzeu-la
amb un ombrejat Gouraud;
el resultat és aquest, molt similar a un dònut: |
| |
|
| |
|
| |
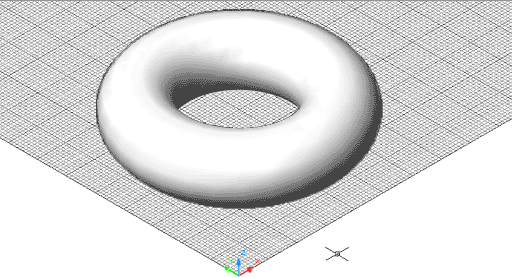
Figura 12. El mateix toroide, visualitzat amb un ombrejat
Goraud
|
| |
|
| |
Algunes consideracions importants
sobre els sòlids |
| |
|
|
|
Abans de donar per finalitzada aquesta pràctica, s'han de tenir
en compte un parell de consideracions importants respecte als sòlids:
- Els sòlids, malgrat el seu nom, no són objectes impenetrables;
podeu crear objectes sòlids que s'intersequin amb altres sòlids.
|
| |
|
| |
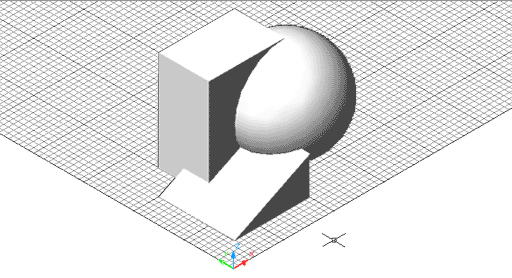
Figura 13. Prisma rectangular, cunya i esfera sòlides
intersecades
|
| |
|
| |
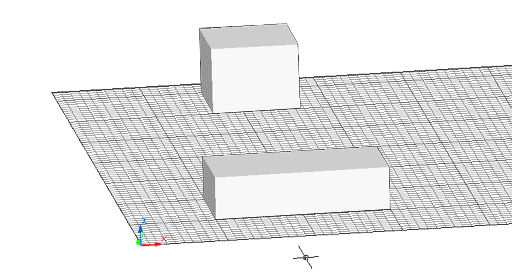
- A l'espai de dibuix 3D de l'AutoCAD 2002
no hi ha cap llei de la gravetat; els objectes, del tipus que sigui
-i els sòlids que estan inclosos en aquesta categoria- poden
"surar" per sobre altres objectes o sobre el pla de terra
indicat per la Rejilla sense cap mena
de problema.
|
| |
|
| |
Figura 14. A l'espai de dibuix de l'AutoCAD no hi ha llei de la gravetat;
els objectes poden surar a l'espai
|
| |
|
| |
Un cop enteses aquestes consideracions,
tanqueu el document sense guardar els canvis i sortiu del programa. |
| |
|
| |
|
 |
| |
|
| |
|