Enrera
 Mòdul 6
Dibuix tècnic amb l'AutoCAD
  Pràctica
1
2
3
4
5
6
   
Exercicis
Exercicis
 
 

La present pràctica vol presentar les principals manipulacions de sòlids: Empalme, Chaflán, Corte, Sección i Interferencia.
   
  Modificacions simples de sòlids
 
Empalmament aplicat a sòlids
   

L'ordre de modificació Empalme, de la mateixa manera que podia ser aplicada a objectes 2D, també pot ser aplicada a les arestes dels sòlids.

 
Atenció !
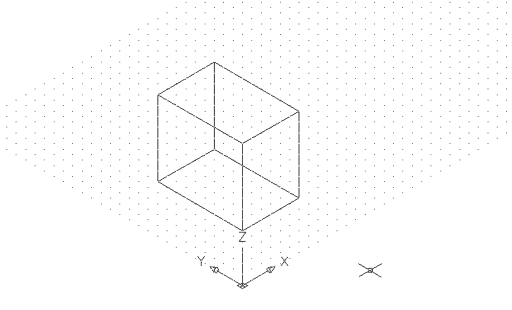
 Abans d'executar l'ordre, obriu un document nou de les característiques habituals i feu un prisma de base rectangular de 60 x 90 unitats de dibuix de base i 90 unitats de dibuix d'alçada. A continuació, visualitzeu l'espai de dibuix des de la perspectiva isomètrica SO, amb un ombrejat de filferro 2D:
   
 
 
Figura 1
   

Ara, apliqueu un Empalme a alguna de les arestes dels prisma:

  1. Escriviu empalme a la barra de comandaments i premeu la tecla de Retorn.
  2. La barra de comandaments us demana Designe el primer objeto o [Polilínea/RAdio/Recortar]:. Seleccioneu una aresta del prisma i la barra de comandaments us indicarà Indique radio de empalmae <10.0000>: premeu la tecla de Retorn per acceptar aquest valor.
  3. La barra de comandaments us demana Designe una arista o [Cadena/Radio]:. Si seleccioneu arestes, en el moment d'executar l'empalme, totes patiran la mateixa modificació de radi 10; si seleccioneu l'opció Radio -r i tecla de Retorn-, podreu modificar el radi de l'empalmament i continuar seleccionant arestes. Seleccioneu les quatre arestes de la cara superior del prisma i premeu la tecla de Retorn.

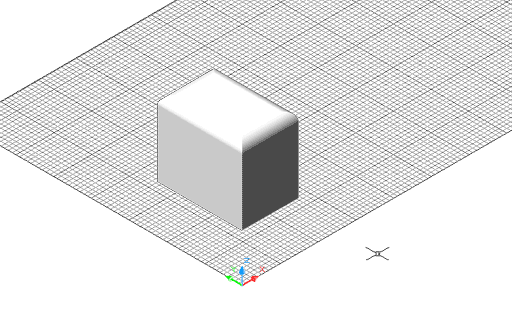
El resultat és aquest -vist amb un ombrejat Gouraud:
   
 
 
Figura 2. Prisma amb empalmament a les arestes de la cara superior, vist amb un ombrejat Gouraud
   
  Xamfrà aplicat a sòlids
   

Tal com succeïa amb l'ordre Empalme, també l'ordre Chaflán pot ser aplicada a les arestes dels sòlids, de manera molt similar a com s'aplica als objectes 2D.

 

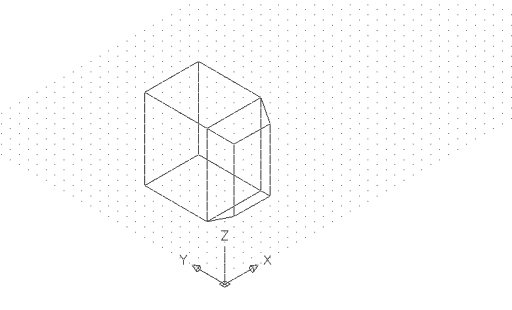
Desfeu l'aplicació de l'empalmament a la figura anterior, i apliqueu el xamfrà:

  1. Escriviu chaflan a la barra de comandaments i premeu la tecla de Retorn.
  2. La barra de comandament us demana Designe la primera línea o [Polilínea/Distancia/ángUlo/Recortar/Método]:. Seleccioneu una aresta qualsevol, per exemple una de la cara que teniu en primer terme.
  3. Ara el programa us diu Indique opción de selección de superficie [Siguiente/Aceptar] <Aceptar>:. Si premeu la tecla de Retorn, donareu per vàlid el pla actualment seleccionat; si premeu s i la tecla de Retorn, el programa anirà indicant els plans successius fins que accepteu. De moment, premeu la tecla de Retorn i accepteu el pla actualment seleccionat.
  4. Ara el programa demana Precise superficie de base distancia de chaflán <10.0000>:. Aquesta és la profunditat del xamfrà sobre la cara seleccionada. Premeu la tecla de Retorn per acceptar-la.
  5. La pregunta següent és Precise otra superficie distancia de chaflán <10.0000>:. Aquesta és la profunditat del xamfrà a les cares adjacents; escriviu 20 i premeu la tecla de Retorn.
  6. Per últim, el programa us demana Designe una arista o [Bucle]:. Podeu seleccionar una a una les arestes sobre les quals aplicar el xamfrà i prémer la tecla de Retorn, o bé seleccionar l'opció Bucle per indicar al programa que selecionareu de cop tot el perímetre d'una cara per aplicar-hi un xamfrà. Seleccioneu l'opció Bucle -b i tecla de Retorn-, un pla i després premeu la tecla de Retorn.

El resultat ha de ser més o menys com aquest:
   
 
 
Figura 3. Resultat de l'aplicació del xamfrà, amb ombrejat d'estructura de filferro 2D
   
  Tall
   

L'ordre Corte permet tallar un o diversos sòlids a partir d'un pla, que pot ser un predeterminat -paral·lel a XY, YZ, ZX o bé pot ser definit al moment.

 

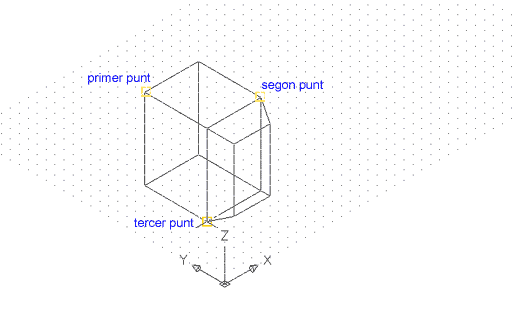
L'ordre Corte pot ser definida de tres maneres:

  • Prement el botó Corte de la barra d'eines Sólidos.
  • Menú Dibujo|Sólidos|Corte.
  • Escrivint corte a la barra de comandaments i prement la tecla de Retorn.
  1. Executeu l'ordre Corte.
  2. A Designe objetos: seleccioneu l'objete/s que s'ha de tallar; seleccioneu el sòlid anterior i premeu la tecla de Retorn.
  3. Ara el programa us demanarà el mètode de tall: Precise primer punto en plano cortante mediante
    [Objeto/ejeZ/Vista/XY/YZ/ZX/3puntos] <3puntos>:    ; premeu la tecla de Retorn per acceptar el mètode 3 punts, que us permet definir al moment el pla a partir del qual tallar el sòlid.
  4. Ara us anirà demanant Precise primer punto en plano: , Precise segundo punto en plano: i Precise primer tercer en plano:; fent servir la referència a objectes Punto final, indiqueu fent clic els tres punts que us mostra la imatge següent:
 
 
Figura 4. Definició dels tres punts per fer un tall en el sòlid; en realitat, l'ordre de determinació dels punts no té importància
   
 
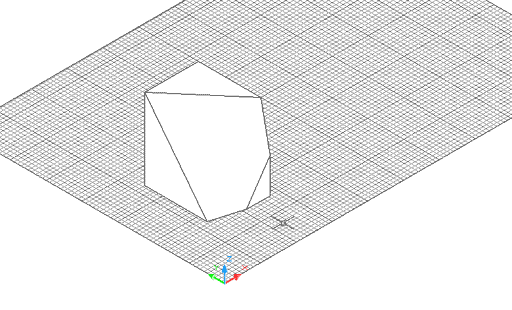
  • Per últim, el programa us demana Precise un punto en lado deseado o [mantener Ambos lados]:. Heu de fer clic en un punt qualsevol del costat que voleu mantenir del sòlid -l'altra part fruit del tall serà eliminada- o bé triar l'opció Ambos lados -a i premeu la tecla de Retorn-, de manera que el sòlid quedarà dividit en dos parts, sense eliminar cap de les dues. Feu clic en la cantonada més allunyada de la cara superior que queda entre el primer i el segon punt indicats anteriorment, i observeu el resultat amb un ombrejat Líneas ocultas:
 
 
Figura 5. Resultat del tall amb pla de tall definit per tres punts, mantenint una part del sòlid
   
Atenció !
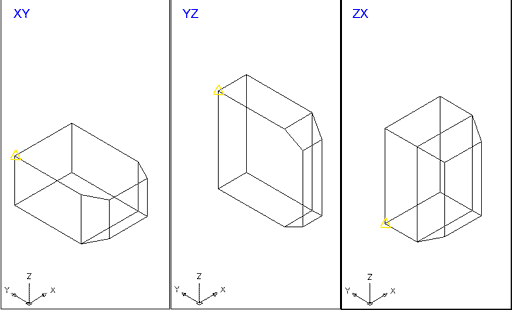
 Si a l'hora de triar el mètode opteu per qualsevol dels mètodes XY, YZ o ZX, heu de tenir en compte que els plans es definiran en relació amb la posició de la icona SCP; d'altra banda, només heu de definir un punt en l'objecte pel qual passarà el pal de tall:
   
 
 
Figura 6. Resultat de talls mitjançant plans paral·lels a XY, YZ i ZX, i els punts pels quals han passat -evidentment, aquí es mostra només una de les dues possibles meitats que s'han de mantenir
   
  Secció
   
Atenció !
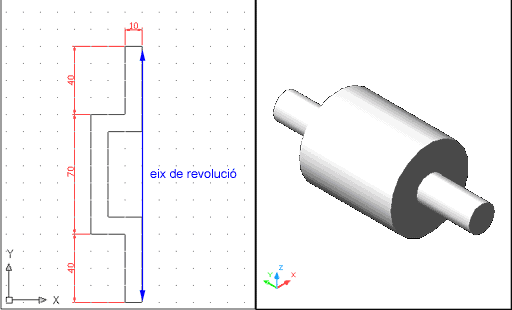
 Abans de començar, esborreu el sòlid anterior i dibuixeu una polilínia de les mesures següents i revolucioneu-la sobre un eix paral·lel a Y per obtenir un sòlid com el que es mostra a la dreta de la imatge següent:
   
 
 
Figura 7. Polilínia i sòlid fruit de la seva revolució vist amb ombrejat Gouraud des de la perspectiva isomètrica SO
   

L'ordre Sección permet obtenir una polilínia 2D amb la forma de la secció d'un sòlid, a partir d'un pla de secció. Els mètodes per definir aquest pla són els mateixos que fèieu servir per definir el pla de tall amb l'ordre Corte.

 

L'ordre Sección pot ser definida de tres maneres:

  • Prement el botó Sección de la barra d'eines Sólidos.
  • Menú Dibujo|Sólidos|Sección.
  • Escrivint seccion a la barra de comandaments i prement la tecla de Retorn.
  1. Executeu l'ordre Corte.
  2. A Designe objetos: seleccioneu l'objecte sobre el qual s'ha d'aplicar una secció; seleccioneu el sòlid i premeu la tecla de Retorn.
  3. Ara el programa us demana el mètode de tall: Precise primer punto en plano de sección mediante
    [Objeto/ejeZ/Vista/XY/YZ/ZX/3puntos] <3puntos>:     ;premeu la tecla de Retorn per acceptar el mètode de tres punts.
  4. Ara us anirà demanant Precise primer punto en plano: , Precise segundo punto en plano: i Precise primer tercer en plano:; fent servir la referència a objectes Cuadrante, indiqueu amb un clic els tres punts que us mostra la imatge següent:
 
 
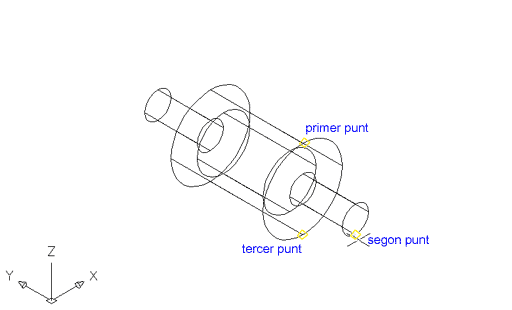
Figura 8. Definició dels tres punts per fer una secció del sòlid; l'ordre de determinació dels punts no té importància
   
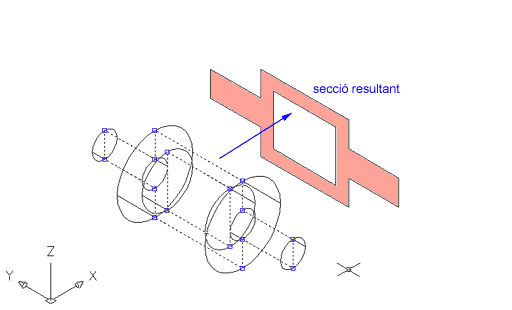
  La secció ja està feta; seleccioneu-la i moveu-la per veure-la millor:
   
 
 
Figura 9. Secció resultant
   
Atenció !
 Com podeu veure, la secció us permet representar sobre un pla l'espai buit de l'interior del sòlid, acotar-lo amb facilitat, etc.
   
  Interferència
   
Atenció !
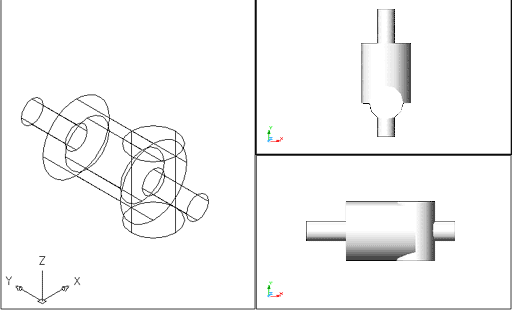
 Abans d'aplicar l'ordre Interferencia, feu un sòlid -per exemple, un cilindre- el volum del qual s'intersequi amb el de la figura anterior tal com mostra la imatge següent:
   
 
 
Figura 10. Vista isomètrica SO amb ombrejat de filferro 2D i planta i perfil amb ombrejat Gouraud dels dos sòlids intersecats
   

L'ordre Interferencia permet crear un sòlid fruit de la intersecció de dos o més sòlids preexistents.

 

L'ordre Interferencia pot ser definida de tres maneres:

  • Premet el botó Sección de la barra d'eines Sólidos.
  • Menú Dibujo|Sólidos|Interferencia.
  • Escrivint interf a la barra de comandaments i prement la tecla de Retorn.
  1. Executeu l'ordre Interferencia.
  2. A Designe objetos: seleccioneu un dels dos sòlids i premeu la tecla de Retorn.
  3. Ara el programa us torna a demanar Designe objetos:. Seleccioneu l'altre sòlid i premeu la tecla de Retorn.
  4. Per últim, el programa us demana ¿Crear interferencia de sólidos? [Sí/No] <N>:. Teclejeu la lletra s i la tecla de Retorn.

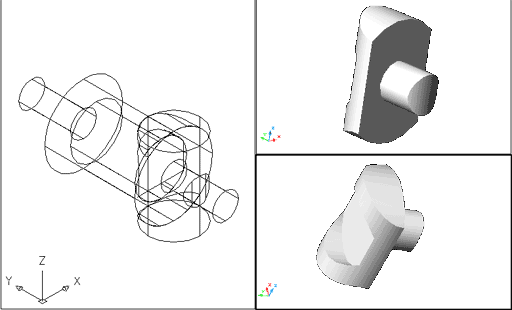
La interferència ha estat executada; moveu el sòlid resultant per veure'l millor:
   
 
 
Figura 11. Interferència dins dels sòlids que l'han originat, i dues vistes amb ombrejat Gouraud del sòlid -interferència en solitari
   
  Un cop fet, tanqueu el document amb el nom m6_pr6 a la carpeta Practiques i sortiu del programa.
   
 
Amunt