Enrera
 Mòdul 6
Dibuix tècnic amb l'AutoCAD
  Pràctica
1
2
3
4
5
6
   
Exercicis
Exercicis
 
 

Aquesta pràctica us permetrà conèixer les diferents operacions booleanes que poden aplicar-se als sòlids i practicar-les.
   
  Operacions booleanes amb sòlids
 

Tal com heu vist a la pràctica segona d'aquest mateix mòdul, les booleanes són operacions que permeten sumar, restar o interseccionar espais.

Si abans havíeu vist aquestes operacions aplicades a les regions, ara veureu com les esmentades booleanes poden ser aplicades també als sòlids.

   
Operació booleana Unión aplicada a sòlids
   
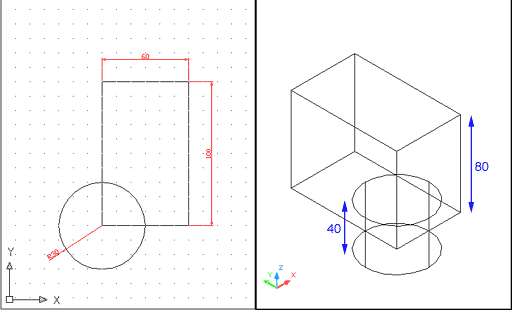
Obriu un document nou de característiques habituals i feu un parell de sòlids com els que es mostren a la figura següent:
   
 
 
Figura 1. Vista superior i isomètrica SO amb ombrejat d'estructura de filferro 3D de dos sòlids: un prisma de base rectangular i un cilindre. Fixeu-vos que el centre de la base del cilindre coincideix amb un dels vèrtexs de la base del prisma
   
 

L'ordre Unión es pot executar de tres maneres:

  • Porement el botó Unión de la barra d'eines Editar sólidos.
  • Menú Modificar|Editar sólidos|Unión.
  • Escrivint union a la barra de comandaments i prement la tecla de Retorn
  1. Executeu l'ordre.
  2. La barra de comandaments us demana Desgine objetos:. Seleccioneu tots dos objectes i premeu la tecla de Retorn.

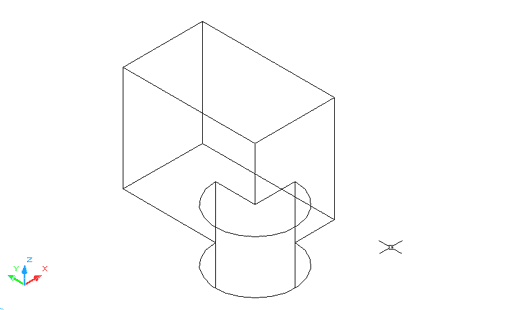
L'ordre ha estat executada i el resultat és un únic sòlid amb l'aspecte dels dos anteriors:
   
 
 
Figura 2. Resultat de la unió dels dos sòlids
   
Atenció !
 També podeu fer la unió simultània de diversos sòlids; fins i tot, el sòlid resultant d'una operació d'unió pot ser posteriorment unit a nous sòlids, etc., sense cap mena de restricció.
   
Operació booleana Diferencia aplicada a sòlids
   

Desfeu el pas anterior fins a tenir de nou dos sòlids diferents i comproveu el funcionament de la booleana Diferencia:

L'ordre Diferencia pot ser executada de tres maneres:

  • Prement el botó Diferencia () de la barra d'eines Editar sólidos.
  • Menú Modificar|Editar sólidos|Diferencia.
  • Escrivint diferencia a la barra de comandaments i prement la tecla de Retorn.
  1. Executeu l'ordre.
  2. La barra de comandaments us demana Designe sólidos y regiones de las que sustraer... - Desgine objetos:. Seleccioneu l'objecte al qual restareu el volum, per exemple seleccioneu el prisma i premeu la tecla de Retorn.
  3. La pregunta següent és Designe sólidos y regiones a sustraer... - Desgine objetos:. Seleccioneu el volum que s'ha de restar, en aquest cas el cilindre, i premeu la tecla de Retorn.

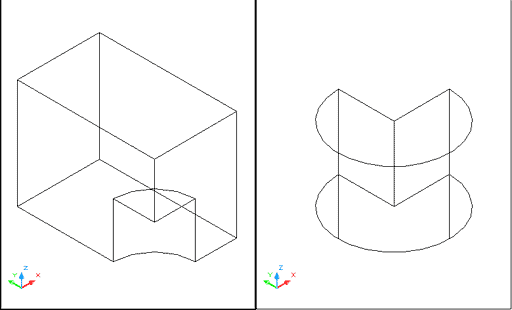
El resultat correspon a la imatge de la vostra esquerra; a la dreta, es mostra el resultat de la sostracció del volum del prisma al del cilindre:
   
 
 
Figura 3. Resultat de la sostracció del volum del cilindre al del prisma, i viceversa
   
Atenció !
 Com en el cas de la Unión, amb la Diferencia també podeu triar diversos sòlids com a elements dels quals restar o bé diversos sòlids o tant una cosa com l'altra.
   
Operació booleana Intersección aplicada a sòlids
   

Una vegada més, desfeu el pas anterior i comproveu el funcionament de la booleana Intersección:

L'ordre Intersección es pot executar de tres maneres:

  • Prement el botó Intersección de la barra d'eines Editar sólidos.
  • Menú Modificar|Editar sólidos|Intersección.
  • Escrivint intersec a la barra de comandaments i prement la tecla de Retorn.
  1. Executeu l'ordre.
  2. La barra de comandaments us demana Desgine objetos:. Seleccioneu tots dos objectes i premeu la tecla de Retorn.

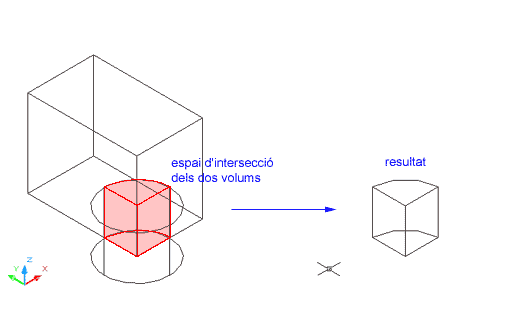
El resultat és un volum corresponent a l'espai d'intersecció dels volums originals, tal com mostra la imatge:
   
 
 
Figura 4. Volum d'intersecció de dos sòlids i resultat -equivalent- de l'operció Intersección
   
Atenció !
 Com en el cas de la Unión, també podeu triar simultàniament diversos volums a l'hora d'operar amb la Intersección, per obtenir un sòlid equivalent a l'espai d'intersecció dels diversos volums.
   
Practicar les operacions booleanes
   
A continuació, treballareu les operacions booleanes fent la figura següent:
   
 
 
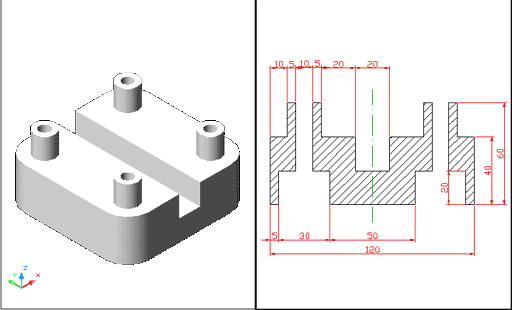Figura 5. Vista isomètrica SO amb ombrejat Gouraud i secció sobre el pla XZ de la figura que s'ha de fer
   
Atenció !
 En primer lloc, obriu un document nou de característiques habituals, i immediatament guardeu-lo com a m6_pr7 a la carpeta de pràctiques.
   
 

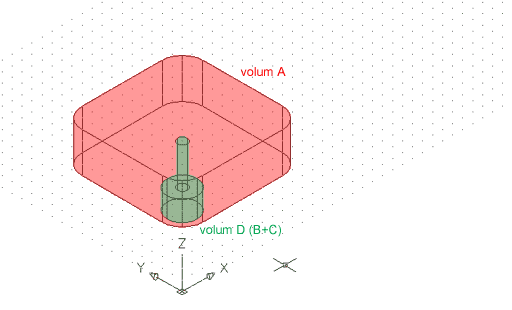
Feu un rectangle amb empalmament de radi 20 (A) de diagonal @120,120. Aquest serà l'espai base dins del qual treballareu, i que esdevindrà després el cos principal de l'objecte.

A continuació, feu un cercle de radi 15 (B) concèntric a l'arc d'empalmament del rectangle, i dins d'aquest un altre cercle concèntric de radi 5 (C).

Extrudiu el rectangle (A) 40 unitats de dibuix, el cercle de radi 15 (B) 20 unitats de dibuix i el de radi 5 (C) 60 unitats de dibuix.

Un cop fet això, feu una Unión dels cilindres (B + C = D).

De moment, el resultat és aquest:
   
 
 
Figura 6
   
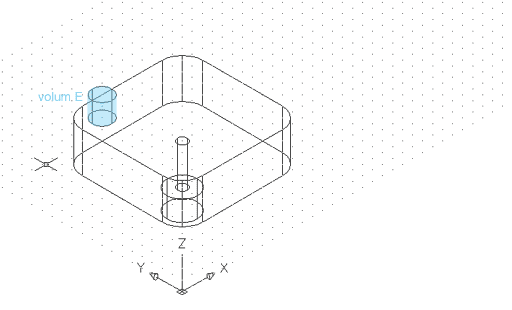
  Ara feu un cilindre de radi 10 i alçada 20 (E) concèntric a l'arc d'empalmament de A a la cara superior de la figura, tal com es mostra a continuació:
   
 
 
Figura 7
   
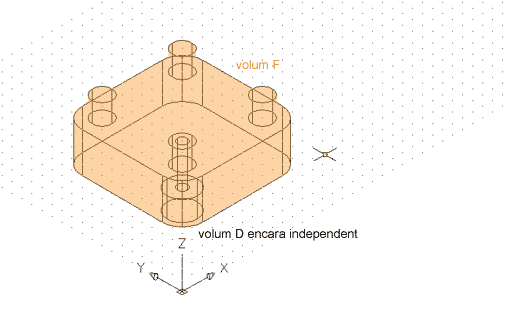
  Copieu tres vegades el volum E a les tres cantonades lliures del volum A, i uniu-les a aquest amb la booleana unió (A + E + E' + E'' + E''' = F).
   
 
 
Figura 8
   
  Ara copieu tres vegades el volum D a les tres cantonades inferiors lliures del volum F i resteu-les a aquest amb l'ordre Diferencia (F - (D, D', D'', D''') = G).
   
 
 
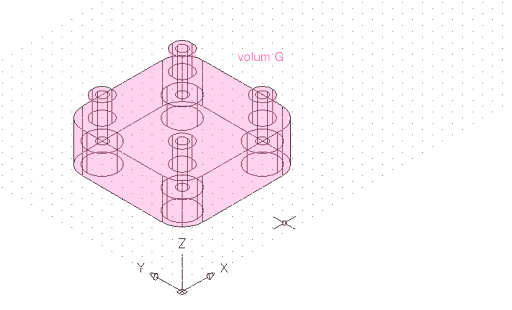Figura 9
   
 

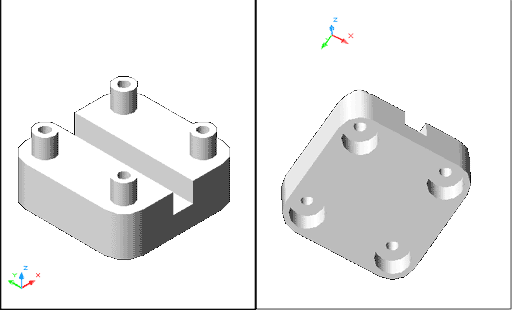
Per últim, feu un prisma de base rectangular (H) de base 20 x 120 (X x Y) unitats de dibuix i
20 d'alçada; col·loqueu-lo al centre de la cara superior del volum G i a continuació resteu-lo a aquest (G - H = final).

Observeu el resultat amb l'Órbita i ombrejat Gouraud, per veure'l per sobre i per sota:
   
 
 
Figura 10. Resultat final
   
  Guardeu els resultats, tanqueu el document i sortiu del programa.
   
 
Amunt