Enrera
 Mòdul 6
Dibuix tècnic amb l'AutoCAD
  Pràctica
1
2
3
4
5
6
   
Exercicis
Exercicis
 
 
 

En aquesta pràctica veureu les ordres Contorno i Región i com fer operacions booleanes amb aquestes, de cara a fer en properes pràctiques objectes 3D a partir d'objectes 2D.
   
Contorn i regió
 
Atenció !

En la present pràctica veureu dos mètodes per transformar els objectes bidimensionals simples en objectes que, potencialment, poden esdevenir objectes tridimensionals sòlids.
   
Contorn
   

L'ordre Contorno permet crear bé una polilínia bé una Región a partir d'un conjunt de línies, arcs o polilínies tancades prèviament existents.

La necessitat de crear una polilínia o una Región està donada per un fet anteriorment esmentat, i és que només els splines i les polilínies tancades -dins de les quals podem incloure cercles, el·lipses i polígons-, les regions i les volanderes poden ser tranformats en objectes sòlids mitjançant els mètodes de l'extrusió i la revolució.
   
Creació d'un contorn senzill a partir d'un conjunt de línies i arcs
   

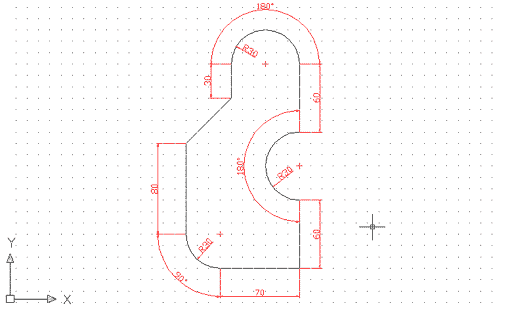
Obriu un document nou de característiques per defecte i dibuixeu amb línies i arcs una figura similar a aquesta, tot ajudant-vos amb la referència a objectes Fin per assegurar-vos que el conjunt és tancat.

Deseu-la a la carpeta Practiques amb el nom m6_pr2.dwg, perquè més endavant la tornareu a fer servir.
   
 
 
Figura 1. Figura tancada feta a base de línies i arcs
   
 

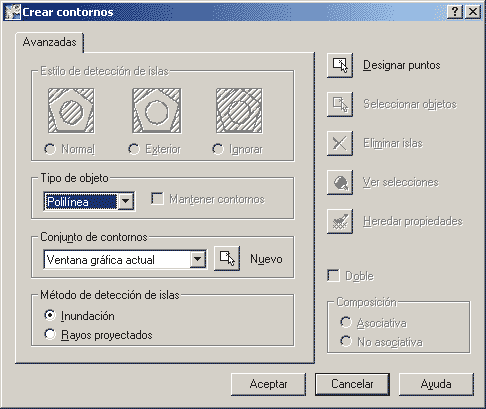
Ara escriviu a la barra de comandament l'ordre contorno i premeu la tecla de Retorn, o bé aneu a buscar l'ordre al menú Dibujo|Contorno...

Immediatament, apareixerà un quadre de diàleg com aquest, anomenat Crear contornos:
   
 
 
Figura 2. Quadre de diàleg Crear contornos
   

Com podeu veure, moltes de les opcions oferides al quadre de diàleg estan desactivades; el motiu és que aquest quadre, en realitat, és una versió simplificada d'un quadre més complex anomenat Sombreado por contornos que en aquest cas no ens serveix.

Les opcions disponibles ara són Tipo de objeto, Conjunto de contornos, Método de detección de islas i Designar puntos.

  • Tipo de objeto permet triar la realització de dos tipus d'objectes contorn: polilínies o regions.
  • Conjunto de contornos permet crear el tipus d'objecte contorn anteriorment seleccionat a partir de tots els perímetres tancats de la finestra gràfica actual, o bé anar triant-los d'un en un fent clic al botó Nuevo.
  • Método de detección de islas, com veurem més endavant, permet crear els objectes contorn tenint en compte els perímetres tancats exteriors i interiors d'una figura -Inundación- o bé tenint en compte només els exteriors -Rayos proyectados.
  • Per últim, el botó Designar puntos serveix per, un cop configurades les opcions anteriors, designar punts interns als perímetres tancats a partir dels quals vulgueu crear un objecte contorn.

 

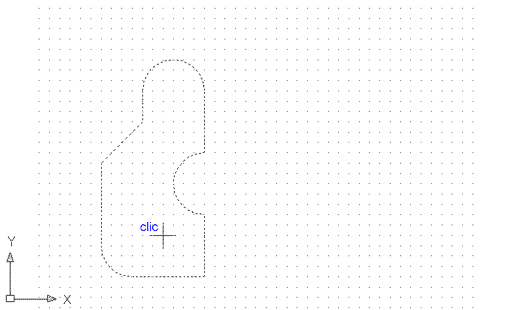
Per veure l'ús de Contorno, trieu com a Tipo de objeto la Polilínea i feu clic directament al botó Designar puntos.

Veureu que immediatament torneu a l'espai de dibuix, amb el missatge següent a la barra de comandaments: Designe un punto interno:. Feu clic amb el punter a l'interior del perímetre de la figura i veureu que:

  1. Aquesta es torna puntejada.
  2. Apareix el missatge Analizando islas internas... a la barra de comandaments.

Un cop fet això, premeu la tecla de Retorn i haureu acabat l'operació; veureu també que el programa, just a la línia superior a la línia Comando: us diu: CONTORNO creado 1 polilínea.
   
 
 

Figura 3. Un cop feu clic al botó Designar puntos, tornareu a l'espai de dibuix. Allí, feu clic a l'interior de la figura tal com se us mostra sobre aquestes línies, i després premeu la tecla de Retorn
 

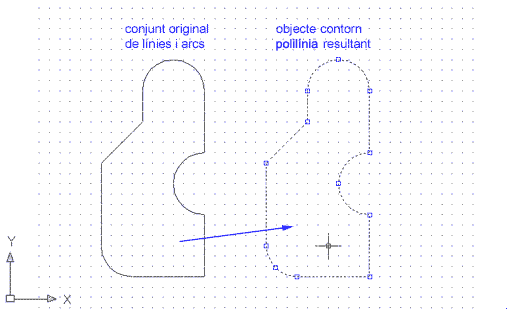
Acabeu de crear una polilínia amb el mateix contorn, o perímetre, que tenia el conjunt de línies i arcs original, sense substituir ni eliminar-lo. Comproveu-ho:

  1. Escriviu desplaza a la barra de comandaments i premeu la tecla de Retorn.
  2. Feu clic sobre un punt qualsevol de la figura i veureu que se selecciona tota; premeu la tecla de Retorn.
  3. Designeu un punt de desplaçament qualsevol i arrossegueu. Veureu que apareixen dos figures iguals. Deixeu la figura arrossegada fent clic a qualsevol punt.

La figura que acabeu d'arrossegar és la polilínia resultant de l'operació Contorno anteriorment efectuada; l'altraés el conjunt de línies i arcs original.
   
 
 
Figura 4. Conjunt de línies i arcs i polilínia resultant de l'operació Contorno. En la figura, la polilínia es mostra discontínua perquè es vegi que, un cop seleccionada, és una única entitat
   
Creació d'un contorn complex
   
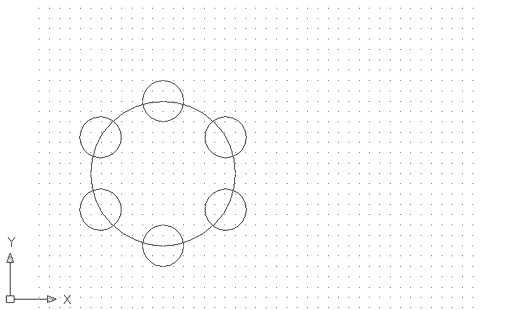
Esborreu la figura anterior i feu-ne una com la següent. Només cal que feu el cercle central i un cercle més petit al quadrant superior; després, feu una matriu polar de sis ítems amb aquest:
   
 
 
Figura 5. Cercle amb sis petits cercles perifèrics intersecats
   
 

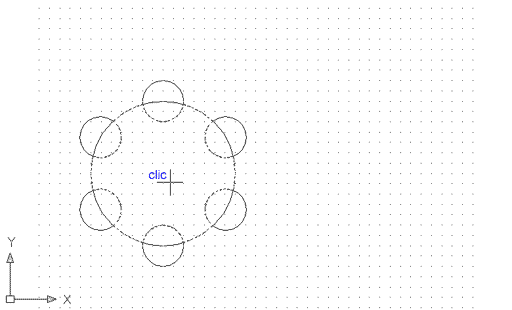
Si en l'exemple anterior heu fet un contorn polilínia a partir d'un contorn tancat de línies i arcs, el que fareu ara serà un contorn complex a partir d'una sèrie de figures que s'intersequen:

  1. Escriviu contorno a la barra de comandaments i premeu la tecla de Retorn.
  2. Al quadre de diàleg Crear contornos, trieu l'opció Polilínea, el mètode Rayos proyectados i feu clic a Designar puntos.
  3. Feu clic a l'interior del cercle principal, tal com s'indica a la figura següent, i premeu la tecla de Retorn.
 
 
Figura 6. Creació d'un contorn polilínia complex a partir de figures intersecades
   
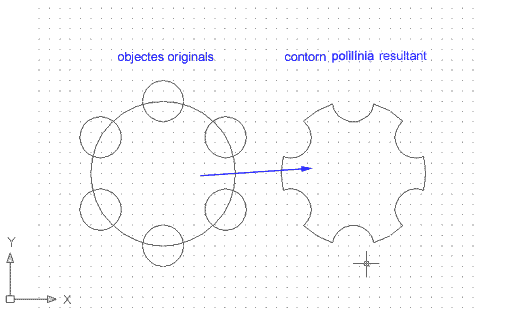
  Ara, com en el cas anterior, desplaceu la polilínia resultant:
   
 
 
Figura 7. Figures intersecades i contorn polilínia resultant
   
 

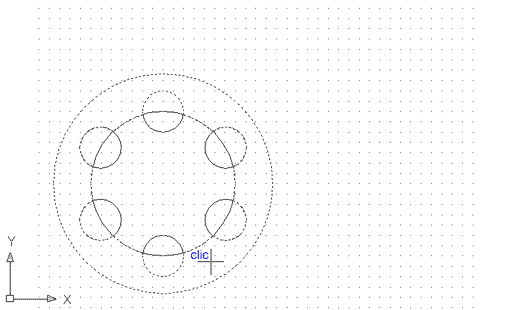
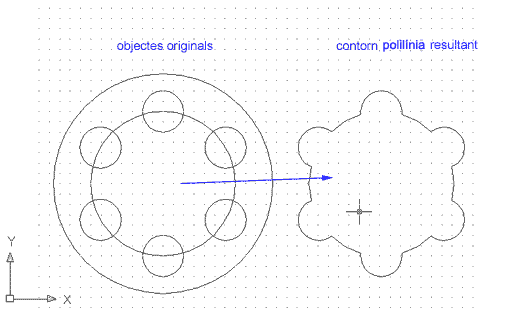
Com veieu, el resultat equival al perímetre del cercle central menys els perímetres intersecats dels cercles perifèrics.

Ara feu-vos aquesta pregunta: puc aconseguir un objecte contorn equivalent al perímetre del cercle central més els perímetres intersecats dels cercles perifèrics? La resposta és que sí.

  1. Esborreu el resultat anterior i dibuixeu al voltant dels cercles un altre cercle -o bé un polígon tancat- de dimensions suficients per incloure tot el conjunt.
  2. Ara escriviu contorno a la barra de comandaments i premeu la tecla Retorn.
  3. Al quadre de diàleg Crear contornos trieu l'opció Polilínea, el mètode Inundación i feu clic a Designar puntos.
  4. Feu clic a l'interior del cercle principal, tal com s'indica a la figura següent, i premeu la tecla de Retorn.
 
 
Figura 8. Creació d'un nou contorn polilínia complex a partir de figures intersecades dins una figura general
   
  De nou, desplaceu la polilínia resultant:
   
 
 
Figura 9. Figures intersecades i contorn polilínia intern -Inundación- resultant
   
  Com que el mètode triat era Inundación, el programa ha creat un contorn extern -el cercle envolupant- i alhora un contorn intern -el resultat. El cercle perifèric també té el seu contorn polilínia superposat, però en aquest cas, no us interessa.
   
Regió
   
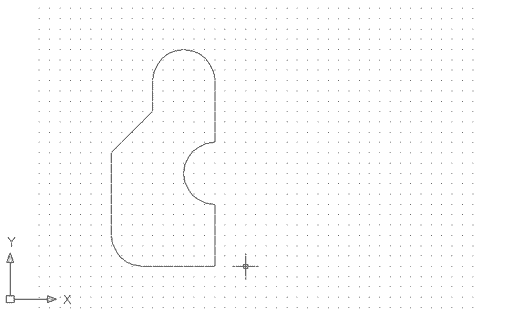
  Torneu a obrir l'arxiu m6_pr2.dwg, on hi ha la figura feta amb línies i arcs que heu fet servir a l'inici de la pràctica:
   
 
 
Figura 10. Figura feta d'arcs i línies
   
 

Transformeu aquesta figura, feta a base de línies, en una regió. A diferència del contorn, la regió no crea un duplicat, sinó que substitueix l'objecte original.

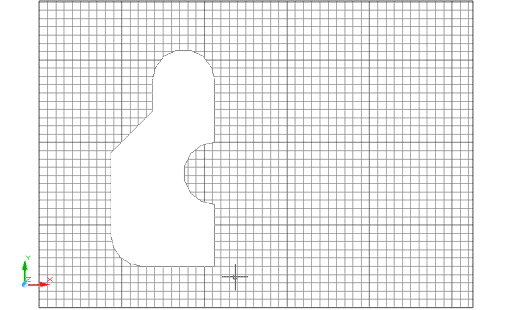
  1. Escriviu region i premeu la tecla de Retorn.
  2. La barra de comandament us demana Designe objectos:. Amb el punter, seleccioneu tots els objectes -d'un en un o amb un marc de selecció- i després premeu la tecla de Retorn.

Ja heu creat una nova regió. A diferència del contorn, la regió no és un perímetre: és un pla. Podeu comprovar-ho visualitzant l'espai de dibuix sota un ombrejat pla o un Gouraud:
   
 
 
Figura 11. Regió vista amb un ombrejat Gouraud
   
Operacions booleanes amb regions
   

Les regions, en ser plans, permeten fer operacions booleanes entre elles; es poden sumar les àrees de dues o més regions, es pot sostreure l'àrea d'una o més regions a una altra, i es pot obtenir una àrea fruit de la intersecció de dues o més regions.
   
  Suma de regions
   
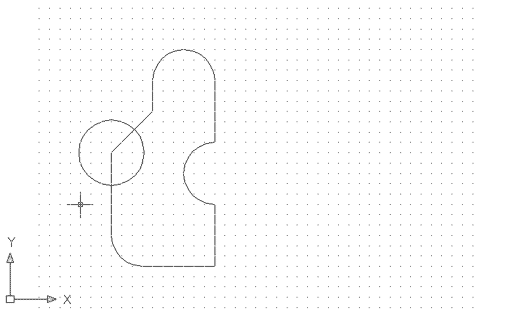
A la figura anterior, afegiu-hi el següent cercle, i transformeu-lo en una regió, tal com es mostra a la imatge següent; és molt important, per estalviar-vos problemes, que visualitzeu totes les operacions que fareu a partir d'ara amb un ombrejat de filferro 2D:
   
 
 
Figura 12. Dues regions, una a sobre de l'altra, vistes amb un ombrejat d'estructura de filferro 2D
   
 
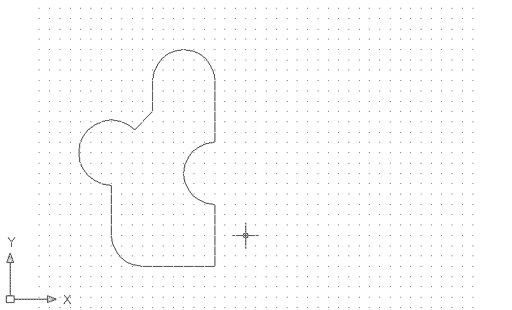
  1. Ara escriviu union a la barra de comandament i premeu la tecla de Retorn.
  2. La barra de comandament us demana Designe objetos:. Seleccioneu les dues regions i premeu la tecla de Retorn.

El resultat és aquest:
   
 
 
Figura 13. Dues regions, sumades mitjançant una operació booleana
   
Resta de regions
   
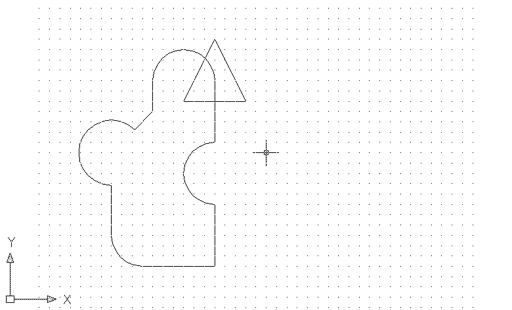
Dibuixeu ara un triangle amb tres línies independents, tal com es mostra a la figura 12, i transformeu el conjunt de línies en una regió:
   
 
 
Figura 12: De nou, dues regions, una a sobre de l'altra, intersecant-se
   
 
  1. Ara escriviu diferencia a la barra de comandament i premeu la tecla de Retorn.
  2. La barra de comandament us demana Designe sólidos y regiones de las que sustraer... i a sota Designe objetos:. Seleccioneu la regió a la qual s'ha de sostreure la superficie de l'altra regió, per exemple, seleccioneu la regió major, i premeu la tecla de Retorn.
  3. Ara la barra diu Designe sólidos i regiones a sustraer... i a sota Designe objetos:. Seleccioneu la regió triangular i premeu la tecla de Retorn.

El resultat és aquest:
   
 
 
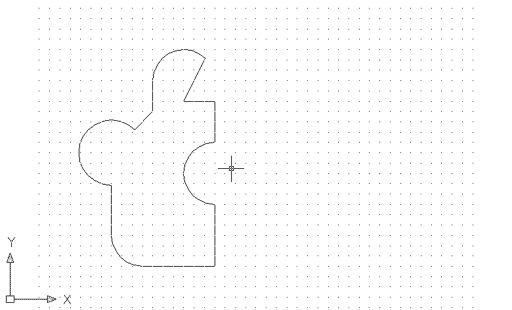Figura 15. Resultat de la sostracció booleana d'una regió a una altra
   
Intersecció de regions
   
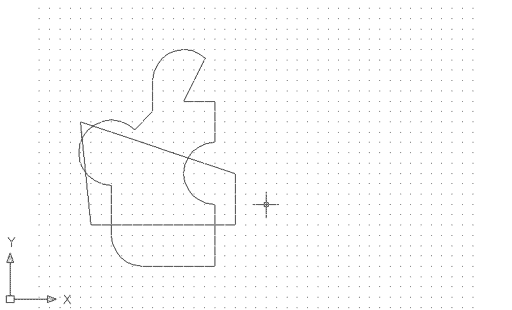
Ara dibuixeu un quadrilàter semblant al que mostra la figura 16 i transformeu-lo en una regió:
   
 
 
Figura 16. Una vegada més, dues regions intersecant-se
   
 
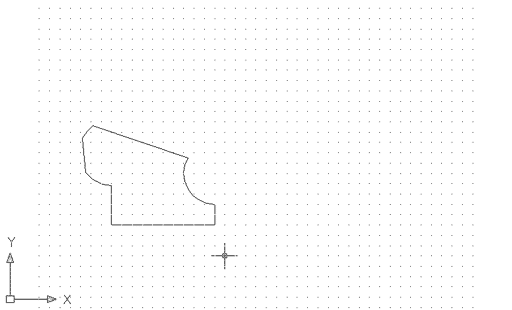
  1. Ara escriviu intersec a la barra de comandaments i premeu la tecla Retorn.
  2. El programa us demana Designe objetos:. Seleccioneu totes dues regions i premeu la tecla de Retorn.

El resultat és una regió com aquesta:
   
 
 
Figura 17. Resultat de la intersecció booleana de dues regions
   
Atenció !
 També podeu crear regions a partir d'un conjunt de línies, arcs, polilínies, etc., tancat des del quadre de diàleg Crear contornos; només cal que trieu com a Tipo de objeto la Región en lloc de Polilínea. El procediment és idèntic al de la creació d'objectes contorn polilínia.
   
  Un cop fet, tanqueu el document sense desar els canvis i sortiu del programa.
   
 
Amunt