|
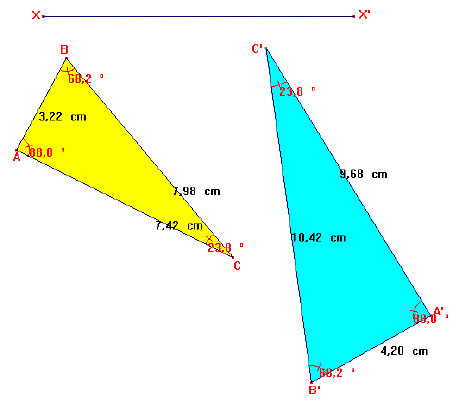
Dos triangles que tenen els seus angles iguals tindran la mateixa forma.
Podran diferir en grandària, però visualment els veurem semblants. Però la
paraula semblant té, en aquest cas, un significat matemàtic afegit:
semblant vol dir també proporcional. Això és degut a que si dos triangles
són semblants els seus costats corresponents seran proporcionals. Pots
comprovar-ho pitjant sobre la imatge i obrint aquesta animació:
- els dos triangles són semblants (tenen els angles iguals, per tant
la mateixa forma)
- pots variar el triangle ABC movent els seus vèrtex
- pots canviar la posició del triangle A'B'C' movent A' o
B'
- pots canviar la mida de del triangle A'B'C' canviant la longitud del
segment XX'
- anota les mesures i comprova que la relació de proporcionalitat no
varia.
- prova diferents casos.
|
| Aquesta propietat dels triangles semblants és conseqüència directa
de l'aplicació del Teorema de Tales. El seu possible autor, Tales de
Milet, va ser segurament el primer (en el temps) dels grans
matemàtics grecs. Era d’origen fenici i residia a Milet, una
pròspera ciutat grega de l’Àsia Menor. Procedia d’una família de
comerciants i, per aquest motiu, va realitzar freqüents viatges a
Egipte, la qual cosa el va animar a l’estudi dels fenòmens naturals i
de la geometria. No ens ha arribat cap escrit seu, per tant no sabem
del cert si el Teorema que porta el seu nom és seu. Sí que sabem, en
canvi, que el va simplificar i utilitzar en moltes i diferents
situacions, com ara calcular l’alçada de diferents edificis o les
distàncies dels vaixells a la costa. En geometria es consideren seves
les demostracions que en un triangle isòsceles hi ha dos angles
iguals, o que un diàmetre divideix un cercle en dues parts iguals,
entre d’altres. També és famós per haver predit amb encert un eclipsi
de Sol l’any 585 a.n.e. |
 |
|
Hi ha moltes llegendes sobre el caràcter de Tales que, normalment, el
presenten com un home esquerp. No serà així en aquestes que t’explicarem
ara.
| El granger i el ruc que no volia anar carregat Un pagès
que sovint havia d’anar al mercat a vendre càrregues de sal va
observar que cada vegada que passaven el riu que separava casa seva de
la ciutat, l’ase s’inclinava i remullava els sacs. D’aquesta manera.
part de la sal es dissolia a l’aigua i el ruc es notava més lleuger.
Fart d’aquestes pèrdues de sal i sense saber què fer el pagès va
acudir a consultar Tales. Aquest, després de rumiar una estona, va
donar el següent consell al pagès desconcertat: “Fes el següent viatge
a la ciutat amb els sacs carregats de...”.
T'imagines quin producte li va proposar de carregar?
Amb el
cursor selecciona el requadre de color i sabràs la resposta
|
 |
 |
La piràmide de Khufu S’explica que mentre es trobava
Tales al costat de la Gran Piràmide de Khufu (o Keops, com
l’anomenaven els grecs), s’hi va acostar un sacerdot i li va demanar
que li digués quina era l’altura aproximada de la piràmide. Tales li
va contestar que no la hi volia dir “aproximadament” sinó que
s’estimava més dir-la-hi “exactament”. Per fer-ho, es va estirar sobre
la sorra deixant la marca de l’altura del seu cos al terra. Després va
afegir: “M’estaré aquí quiet fins que la meva ombra coincideixi amb la
marca del terra, és a dir, amb la meva altura. Llavors l’altura de la
piràmide i la seva ombra també coincidiran. Només caldrà mesurar les
passes d’aquesta.” El sacerdot, sorprès, li va demanar si no existia
cap error en el seu raonament. Sense fer gaire cas del que li
qüestionaven, Tales va continuar: “Però, realment, no tinc ganes
d’esperar que el meu cap s’escalfi sota el Sol. Per tant, clavaré el
meu bastó al terra i, quan la mida de la seva ombra sigui la meitat de
la real, l’ombra de la piràmide també ho serà; o quan sigui la tercera
part... N’hi haurà prou a comparar la llargada del bastó i la seva
ombra amb la de l’ombra de la piràmide i multiplicant i dividint
esbrinar la seva altura” |
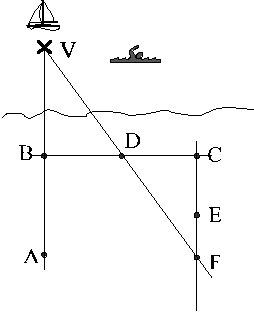
A quina distància es troba el vaixell?
Una altra de les llegendes sobre Tales explica que era capaç de
determinar a quina distància es trobaven els vaixells que s'apropaven
a la costa. Un dels mètodes que es pensa que va poder utilitzar el
tenim representat a l'esquema següent i es podia fer seguint els
següents passos.
- Primer es posaven dues estaques A i B alineades amb el vaixell
que és en un punt que anomenarem V.
- Després es clavava una tercera estaca C formant angle recte amb
la línia AB
- Seguidament es posava una quarta estaca D al punt mig entre B i
C.
- Es clavava una cinquena estaca E fent angle recte amb BC.
- Es caminava seguint la línia CE fins aconseguir veure el vaixell
alineat amb l'estaca D, i es posava una sisena estaca F en aquest
punt
|
|
D'aquesta manera es formen dos triangles rectangles BVD i DCF.
Fem ara unes comparacions:
- Els segments BD i el segment són iguals
- Els angles VBD i DCF també són iguals
- També ho són els angles BDV i CDF
- En conseqüècia els dos triangles BVD i DCF són idèntics
Ara ja ho tenim pràcticament. La distància que volem conèixer és BV.
Quin costat del triangle DCF es correspon amb aquesta mesura?
Amb el
cursor selecciona el requadre de color i sabràs la resposta
|
La distància CF és la mateixa que BV |
Si vols pots comprovar el mètode de Tales obrint
aquesta animació
Aquest mètode té inconvenients claríssims. Un d'ells pot ser que si el
vaixell està a 6 km (en mesures modernes) haurem de mesurar també 6 km
(una mica més d'una hora caminant) en línia recta, sense cap irregularitat
al terreny, sense cap obstacle...
Evidentment el mètode es pot millorar fent més petita la distància DC. Per
exemple, si fem que BD sigui 30 vegades més gran que DC (una manera és fer
30 passes entre B i D i una entre D i C) els triangles que construirem ara
no seran idèntics però sí semblants i podrem aplicar càlculs de
proporcionalitat. El costat del triangle corresponent de terra amb la
distància al vaixell BD també serà 30 vegades més petita.
|




