Introducció

En aquesta pràctica veureu:

• El tractament de la correlació i la regressió lineal entre dues variables.

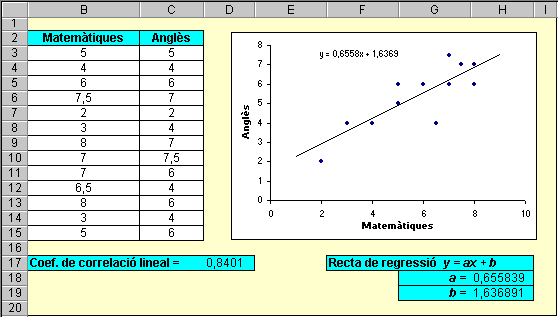
Amb molt poques fórmules podeu calcular, immediatament, el coeficient de correlació lineal i trobar la recta de regressió de Y sobre X, a partir de les dades de les dues variables. 

Evidentment, aquest és un tema molt específic d'estadística i sembla clar que no és el lloc més adient per explicar el seu significat teòric. Creiem, doncs, que aquelles persones que, per la seva especialitat o per la seva dedicació actual, pensin que aquest tema no els és proper, poden abstenir-se de fer aquesta pràctica. 

En canvi, creiem també que pot ser molt útil per al professorat que treballa amb aquests temes, donada la senzillesa amb què aquest programa els tracta. També és interessant veure com el programa permet modificar directament algun punt del núvol de punts i d'aquesta manera es pot observar directament l'efecte que té aquesta modificació sobre el coeficient de correlació lineal i sobre la recta de regressió. 

En el mòdul 7 podreu trobar encara més aplicacions del full de càlcul a l'estadística. 

Un possible exemple pot ser:

Construcció del full de càlcul

Aquí teniu les dades de dues variables, que corresponen a les notes que han tret uns mateixos alumnes en proves de dues assignatures. Es tracta de fer un estudi de la seva correlació lineal i dibuixar la recta de regressió de Y sobre X. 

• Seleccioneu un nou full del llibre MODUL6. Anomeneu-lo Regressió. 
• Introduïu els rètols que veieu a la figura. 
• Modifiqueu l'amplada de les columnes per tal que quedin, aproximadament, com es veu a la figura. 
• Introduïu les dades numèriques del rang B3:C15. 
• Introduïu a la cel·la D17 la fórmula =COEF.DE.CORREL(B3:B15;C3:C15). Aquesta és la funció que serveix per calcular directament el coeficient de correlació lineal. 
• Introduïu a la cel·la H18 la fórmula =PENDIENTE(C3:C15;B3:B15). Aquesta funció calcula el pendent de la recta de regressió de Y sobre X. Fixeu-vos com primer s'ha d'escriure el rang corresponent a la segona variable (Y) i després el de la primera (X). Si ho féssiu al revés sortiria el pendent de la recta de regressió de X sobre Y. 
• Introduïu a la cel·la H19 la fórmula =INTERSECCION.EJE(C3:C15;B3:B15). 
• Aquesta funció calcula el terme independent de la mateixa recta. Aquí també val el comentari fet anteriorment sobre l'ordre d'escriptura dels diferents rangs. 

• Seleccioneu el rang B3:C15 i seguiu el passos habituals per fer els gràfics. Cal tenir en compte els detalls següents: 
• El tipus de gràfic ha de ser XY(Dispersión) amb el suptipus primer de la primera fila. 
• El gràfic no ha de tenir llegenda ni línies de divisió, però sí títols en tots dos eixos. 
• El rang on ha de quedar el gràfic ha de ser el que es veu a la figura. 
• Heu de deixar la zona anomenada Área de trazado sense color ni vores. 
• Podeu canviar el disseny dels punts del gràfic per tal que tinguin una altra forma i mida. 
• Per tal que surti dibuixada la recta de regressió cal clicar sobre els punts del gràfic fins que quedin seleccionats i, a continuació, prémer el botó dret del ratolí. 
• Trieu l'opció Agregar línea de tendencia del menú que ha aparegut. 
• Fixeu-vos en el contingut de la fitxa Tipo. Com podeu veure podríeu triar diferents tipus de regressió. Trieu la Lineal i accediu a la fitxa Opciones. 
• És convenient entrar el nombre 1 en els apartats Extrapolar Hacia adelante i Hacia atrás. D'aquesta manera la recta sobrepassa una unitat per sobre i per sota el núvol de punts. 
• Si voleu que es vegi, com a la figura, l'equació de la recta en el gràfic, cal que activeu l'opció Presentar ecuación en el gráfico. Premeu Aceptar. 
• La recta ja apareix en el gràfic. Si no us agrada el seu disseny, el podeu modificar seleccionant-la, prement el botó dret del ratolí i accedint a l'opció Formato de línea de tendencia. 
• L'equació que surt en el gràfic es pot canviar de lloc seleccionant-la i movent-la amb el ratolí. 
• Podeu modificar la font dels rètols seleccionat-los i triant la mida més convenient de la part superior esquerra de la pantalla (barra d'eines). 

Aneu ara a moure algun punt del gràfic per observar l'efecte que produeix sobre els paràmetres calculats. 

• Feu clic uns quants cops sobre un punt del núvol fins que el cursor es converteixi amb una creu amb fletxes per extrems (com en la pràctica 1 d'aquest mòdul). 
• Premeu el botó esquerre del ratolí i moveu el punt. 
• Quan deixeu anar el botó, el punt quedarà fixat i s'hauran produït canvis numèrics en el full de càlcul. És interessant observar els canvis que es donen en el coeficient de correlació lineal i en el pendent de la recta de regressió segons com es moguin determinats punts. 
• Repetiu més cops aquestes accions i comproveu els canvis que es van produint. 

• Doneu forma i color al full, com es veu a la figura. 
• Deseu el full de càlcul.