A continuació, poseu en pràctica el sistema de definició de punts per coordenades polars.
|
||||||||||||||||
| Pràctica |
Exercicis
|
|||||||||||||||
|
Aquesta pràctica vol continuar desenvolupant l'ordre de dibuix Línea,i introduir els diferents sistemes de definició de punts per coordenades. El coneixement d'aquests sistemes serà fonamental per al desenvolupament de les pràctiques no només d'aquest mòdul, sinó de tots els mòduls del curs. |
|
| Sistemes de coordenades | |
|
|
Un sistema de coordenades serveix per definir punts en un espai amb la màxima precisió. A l'AutoCAD 2002 podreu definir els punts necessaris per fer els vostres dibuixos mitjançant la barra de comandaments, tot tenint en compte les referències que dóna el programa i el sistema de definició de coordenades. L'AutoCAD 2002 accepta dos mètodes per definir punts: mitjançant coordenades cartesianes o rectangulars, i mitjançant coordenades polars. |
| Sistema de coordenades cartesianes o rectangulars | |
|
Per començar a treballar amb els sistemes de coordenades, obriu un nou document amb l'assistent Configuración rápida, tot respectant els valors que us dóna per defecte. Un cop obert el nou document, activeu la Rejilla (F7); us servirà per entendre millor com funcionen els sistemes de definició de punts per coordenades. Assegureu-vos que la Rejilla està configurada en Malla de resolución rectangular, amb un interval en X i Y de 10. |
|
 |
|
|
Figura 1. Aspecte de l'espai de dibuix del nou document.
Si el que veieu en el vostre espai de dibuix és diferent a això,
premeu la tecla z i la tecla de Retorn,
i a continuació la tecla e, i
tecla de Retorn -haureu utilitzat l'eina zoom, de la qual parlarem més
endavant
|
|
|
Com s'havia explicat en pràctiques anteriors, la Rejilla ens delimita visulament l'espai de dibuix, tot mostrant les dimensions del format del document que heu definit. Ara, però, veureu una nova utilitat de la Rejilla: la de permetre la visualització de les referències que el programa utilitza a l'hora de definir punts mitjançant el sistema de coordenades cartesianes absolut. |
|
| Sistema de coordenades cartesianes absolut | |
|
El sistema de coordenades cartesianes absolut té com a referència, en el cas d'un dibuix bidimensional, dos coordenades (X, Y) i un punt d'origen de coordenades (0,0) coincident amb el punt inferior esquerre de la Rejilla. Tots els punts que volguessiu definir fent servir aquest sistema de coordenades cartesianes absolut es definirien a la barra de comandaments amb valors numèrics relatius a X en primer lloc i a Y en segon lloc, separant-los mitjançant una coma: per exemple, 100,150 indicaria la posició d'un punt ubicat a 100 unitats de dibuix sobre X respecte al punt d'origen de coordenades, i 150 unitats de dibuix sobre Y respecte al mateix punt. |
|
|
|
Feu una Línea amb aquest sistema:
|
 |
|
|
Figura 2. Resultat de la seqüència d'ordres
anterior. Com podeu observar, el punt d'origen de coordenades és
coincident amb el punt de la Rejilla, que es troba més baix
i més a la esquerra
|
|
|
|
Podeu donar una coordenada que no sigui un nombre sencer. Per fer-ho, separareu els decimals amb un punt: per exemple, coordenada 100.54; 80.63 El nombre de decimals màxim té relació amb la precisió que heu donat al document a l'hora de configurar-lo. |
|
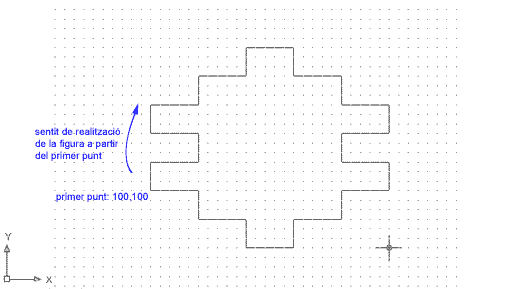
A continuació, esborreu la línia anteriorment traçada i mireu de dibuixar aquesta figura mitjançant el sistema de coordenades cartesianes absolut, tot tenint en compte les dades següents :
|
|
 |
|
|
Figura 3
|
|
|
|
Si us n'heu sortit amb la pràctica, guardeu el document com a m1_pr4a.dwg a la carpeta Practiques. Si no, a continuació teniu la seqüència completa de comandaments per fer la figura; al final de cada línia de comandament, heu de prémer la tecla de Retorn:
|
| Sistema de coordenades cartesianes relatiu | |
|
Com heu pogut comprovar, el sistema de coordenades cartesianes absolut exigeix un càlcul constant de la posició d'un punt respecte al punt d'origen de coordenades, i per això acaba esdevenint massa feixuc. Per aquest motiu, l'AutoCAD 2002 permet treballar amb un altre sistema de definició de coordenades cartesianes molt més àgil i còmode: el sistema de coordenades cartesianes relatiu. El criteri bàsic d'aquest sistema de coordenades cartesianes relatiu també es basa en l'especificació dels punts respecte a X i Y. La diferència radica en què podeu resituar virtualment el punt d'origen de coordenades per evitar el càlcul constant de la posició dels punts respecte a un punt fix. Com indicarem aquesta reubicació virtual del punt 0,0? Molt fàcil: escrivint arrova davant de la coordenada: @x,y.
|
|
|
|
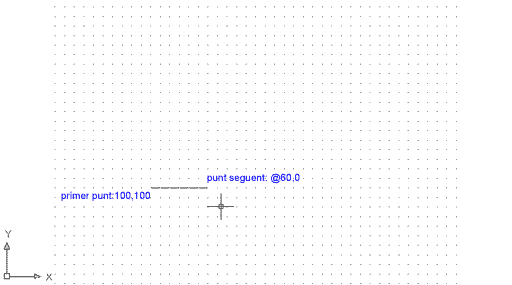
Comproveu-ho:
|
 |
|
|
Figura 4. Resultat de la seqüència d'ordres
anterior. L'arrova fa que el primer punt o punt anterior qualsevol esdevingui,
virtualment, un punt d'origen de coordenades
|
|
|
|
El sistema de coordenades cartesines relatiu és molt més còmode que l'absolut. No obstant això, encara ens resta per aclarir una qüestió fonamental: un cop s'ha definit un punt qualsevol com a 0,0, com es pot determinar una coordenada que no vagi en direcció a X o Y? És a dir: donat un punt d'origen de coordenades, com es pot determinar un segon punt que es trobi a l'esquerra o per sota d'aquell? La resposta és ben senzilla: donant valors negatius bé a X si el punt següent es troba a l'esquerra de l'origen de coordenades, bé a Y si es torba a sota. |
|
|
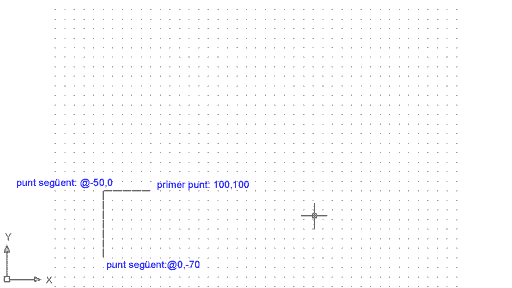
Feu la prova següent:
|
 |
|
|
Figura 5. Resultat de la seqüència d'ordres
anterior. Les coordenades -X situen els punts a l'esquerra de l'origen
de coordenades, mentre que les coordenades -Y els situen per sota
|
|
|
|
Recordeu:
|
|
|
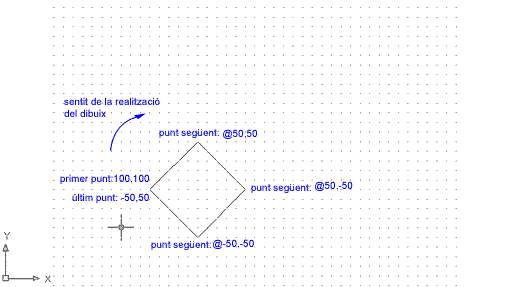
Feu la prova següent:
|
 |
|
|
Figura 6. Resultat de la seqüència d'ordres
anterior
|
|
|
|
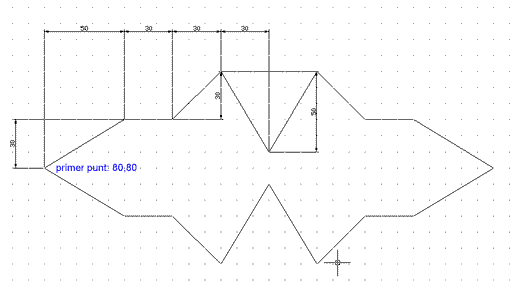
A continuació, esborreu les línies anteriorment realitzades i mireu de dibuixar la figura següent mitjançant el sistema de coordenades cartesianes relatiu.
|
 |
|
|
Figura 7
|
|
|
|
Si us n'heu sortit amb la pràctica, guardeu el document com a m1_pr4b.dwg a la carpeta Practiques. Si no, a continuació teniu la seqüència completa de comandaments per fer la figura:
|
| Sistema de coordenades polar | |
|
Hi ha un tercer mètode per determinar punts en l'espai de dibuix de l'AutoCAD 2002: el sistema de determinació de coordenades polar. A diferència dels dos sistemes anteriorment esmentats, el polar ens permet treballar amb mesures absolutes de segments i angles. És a dir, amb el sistema de coordenades polar, no donarem la posició d'un punt mitjançant X, Y, sinó que determinarem la distància i l'angle relatiu d'un punt respecte a un primer. |
|
|
|
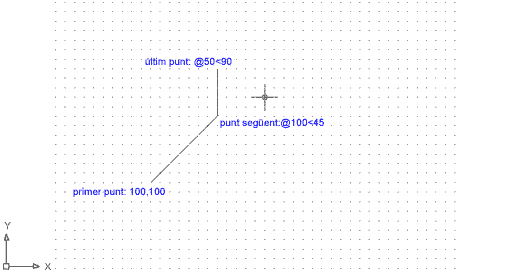
Obriu un nou document tal com heu fet fins ara, amb les mesures habituals, i feu la prova següent:
|
 |
|
|
Figura 8. Resultat de la seqüència d'ordres anterior |
|
|
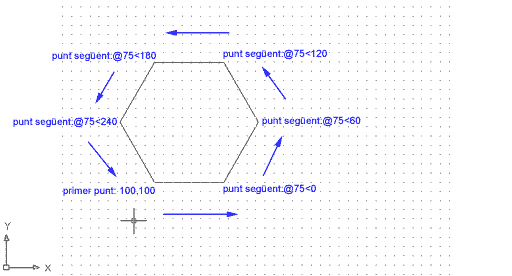
A continuació, poseu en pràctica el sistema de definició de punts per coordenades polars.
|
|
 |
|
|
Figura 9
|
|
|
|
Guardeu el resultat amb el nom m1_pr4c.dwg a la carpeta Practiques. Si no ho heu aconseguit, aquí teniu la seqüència completa d'ordres per resoldre la figura:
|
|
|
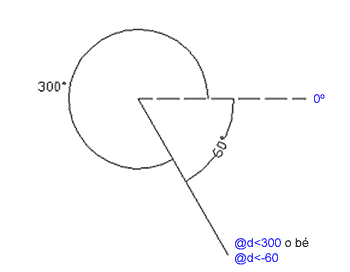
Com heu comprovat, el sistema de coordenades polar determina els punts mitjançant la fórmula @ mesura del segment < angulació (en sentit antihorari). També podeu determinar un punt localitzant-lo en sentit horari: @ mesura del segment < -angulació (en sentit horari). Així, un segment de mesura determinada (d) per un segon punt @d<300 seria idèntic a un segment @d<-60. |
 |
|
|
Figura 10. Càlcul d'angles en sentit antihorari
-per defecte- o bé en sentit horari, mitjançant les fórmules
@d<angle positiu o bé @d<angle negatiu
|
|
|
|
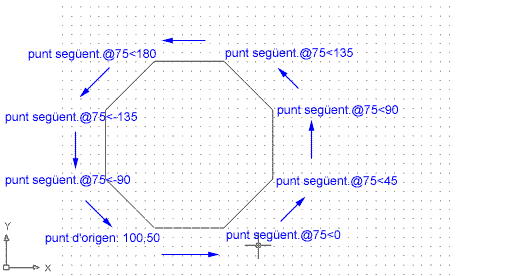
Feu la figura següent en un nou document de característiques habituals, utilitzant el sistema d'angulació horària i antihorària, segons convingui, tot tenint en compte el següent:
|
 |
|
|
Figura 11
|
|
|
|
Guardeu el resultat amb el nom m1_pr4d.dwg a la carpeta Practiques. Si no ho heu aconseguit, aquí teniu la seqüència completa d'ordres per resoldre la figura:
|
| Tanqueu el document i sortiu del programa. | |