Enrera
 Mòdul 1
Dibuix tècnic amb l'AutoCAD
  Pràctica
1
2
3
4
5
6
7
8
    
Exercicis
Exercicis
 
 

Aquesta pràctica pretén introduir l'ordre de dibuix Polígono i les referències a objectes Perpendicular i Cercano.
   
L'ordre de dibuix Polígon i referències a objectes (II)
   
Dibuixar polígons amb l'AutoCAD 2002
   

L'ordre de dibuix Polígono permet dibuixar polígons regulars amb un nombre de cares que va d'un mínim de 3 fins a un màxim de 1.024. Com en el cas dels rectangles, els polígons son objectes polilínia.

L'ordre Polígono pot ser executada de tres maneres:

  • Fent clic al botó corresponent a l'ordre Polígono de la barra d'eines Dibujo .
  • Activant el menú Dibujo|Polígono.
  • Mitjançant la barra de comandaments: poligono i tecla de Retorn.

Un polígon és pot dibuixar a partir de tres mètodes:

  • Determinant el centre i el radi d'una circumferència dins la qual s'inscriurà el polígon.
  • Determinant el centre i el radi d'una circunferència al voltant de la qual es circumscriurà el polígon.
  • Determinant un costat del polígon.
Dibuixar un polígon inscrit en una circumferència
   

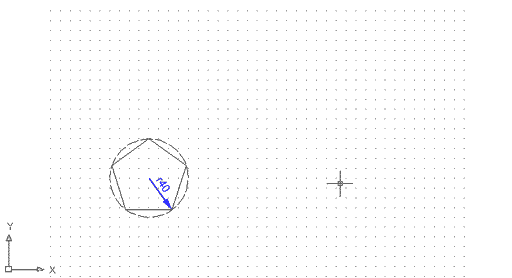
Obriu un nou document com qualsevol del emprats a la pràctica anterior. Podeu activar o no la Rejilla per visualitzar millor l'espai de dibuix i les mesures a les quals ens referirem.

Comproveu el funcionament del primer mètode de creació, l'ordre polígon:

  1. Escriviu poligono a la barra de comandaments i premeu la tecla de Retorn.
  2. Un cop executada l'ordre, la barra de comandaments ens demana el següent: Indique número de lados <4>:.

    Fareu un pentàgon; escriviu 5 i premeu la tecla de Retorn.

  3. La barra de comandaments us demanarà Precise centro de polígono o [Lado]:.

    Introduïu la coordenada 100,100 i premeu la tecla de Retorn.

  4. Un cop indicat el centre, la barra de comandaments us demana Indique una opción [Inscrito en el círculo/Circunscrito alrededor del círculo] <I>:.

    Si premeu la tecla i i la tecla de Retorn o bé la tecla de Retorn directament, triareu fer el polígon inscrit dins d'una circumferència; si premeu c i la tecla de Retorn, el fareu circumscrit. Recordeu que l'opció per defecte és aquella indicada entre <> al final de la pregunta de la barra de comandaments. En aquest cas, trieu l'opció i i premeu la tecla de Retorn.

  5. La pregunta següent de la barra de comandaments és Precise radio del círculo:.

    El que heu d'indicar és la mesura del radi de la circumferència dins la qual s'inscriurà el polígon. Escriviu 40 i premeu la tecla de Retorn.

  6. El polígon està acabat, amb la peculiaritat que un dels seus costats és paral·lel a l'eix X .
 
 
Figura 1. Polígon definit mitjançant el mètode d'inscriure'l dins d'una circumferència. NOTA: la circumferència discontínua només ha estat representada perquè vegeu com funciona aquest mètode. En realitat, vosaltres només veureu el resultat, és a dir, el polígon
   

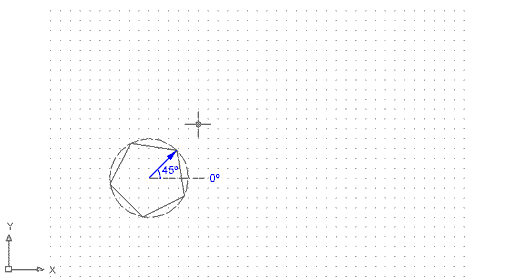
Esborreu el pentàgon anterior; com podeu comprovar, es tracta d'un únic objecte i no de cinc segments de línia independents.

Repetiu la seqüència d'ordres anterior fins a arribar al pas 5. Quan el programa us demani Precise radio del círculo: introduïu una coordenada polar: per exemple, @40<45.

Veureu que el polígon continua estant inscrit en una circumferència de 40 unitats de dibuix de radi, però que aquell costat parlal·lel a l'eix X ara ja no ho és. El programa ha calculat 45º d'inclinació entre el 0º -a l'est- i una línia virtual que passa pel centre i un vèrtex del polígon, tal com mostra la imatge següent.
   
 
 
Figura 2. Polígon definit mitjançant el mètode d'inscriure'l dins d'una circumferència, al qual s'ha donat el radi mitjançant una coordenada polar. NOTA: la circumferència discontínua només ha estat representada perquè vegeu com funciona aquest mètode. En realitat, només veureu el resultat, és a dir, el polígon
   
Dibuixar un polígon circumscrit en una circumferència
   

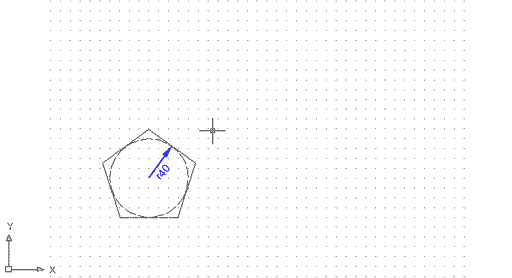
Ara comproveu el segon mètode:

    1. Esborreu el polígon anterior.
    2. Escriviu poligono a la barra de comandaments i premeu la tecla de Retorn.
    3. Un cop executada l'ordre, la barra de comandaments ens demana el següent: Indique número de lados <5>:. Premeu directament la tecla de Retorn.
    4. La barra de comandaments us demanarà Precise centro de polígono o [Lado]:. Indiqueu la coordenada 100,100 i premeu la tecla de Retorn.
    5. Un cop indicat el centre, la barra de comandaments us demana Indique una opción [Inscrito en el círculo/Circunscrito alrededor del círculo] <I>:. Premeu la tecla c i la tecla de Retorn.
    6. A la pregunta de la barra de comandaments Precise radio del círculo: doneu un radi de 40, tot tenint en compte que la indicació feta abans sobre la possibilitat de donar una coordenada és vàlida tant per a polígons inscrits com circumscrits. Premeu la tecla de Retorn.
 
 
Figura 3. Polígon definit mitjançant el mètode de circumscriure'l al voltant d'una circumferència. NOTA: la circumferència discontínua només ha estat representada perquè vegeu com funciona aquest mètode. En realitat, només veureu el resultat, és a dir, el polígon
   
Dibuixar un polígon a partir d'un costat
   

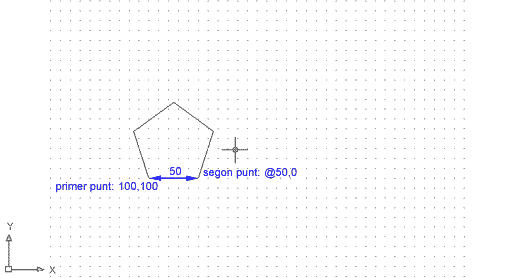
Comproveu el tercer mètode:

    1. Esborreu el polígon anterior.
    2. Escriviu poligono a la barra de comandaments i premeu la tecla de Retorn.
    3. A la pregunta Indique número de lados <5>: premeu directament la tecla de Retorn.
    4. Quan la barra de comandaments us demani Precise centro de polígono o [Lado]: escriviu L i premeu la tecla de Retorn. Ara fareu un pentàgon a partir d'un dels seus costats.
    5. La pregunta següent és Precise primer punt final de lado:. Doneu una coordenada, per exemple 100,100, i premeu la tecla de Retorn.
    6. Ara se us demana Precise segundo punto final del lado:. Doneu una segona coordenada, com si estiguéssiu dibuixant una línia: @50,0 i premeu la tecla de Retorn. Heu dibuixat un pentàgon de costat 50 unitats de dibuix.
 
 
Figura 4. Polígon definit mitjançant el mètode de costat. En realitat, el que definiu és una línia; el programa calcula la resta del polígon
   

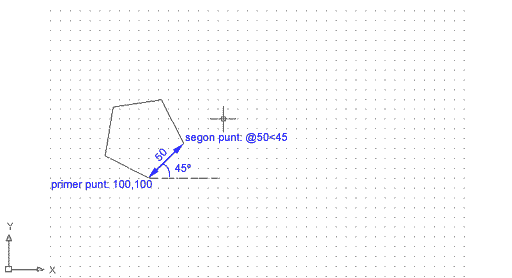
Naturalment, podeu definir la segona coordenada amb el sistema de coordenades polar, perquè la base del polígon tingui una inclinació determinada per vosaltres.

Repetiu el procés anterior fins al pas 5, i quan el programa us demani Precise segundo punto final del lado: escriviu, per exemple, @50<45 i premeu la tecla de Retorn. Tindreu un pentàgon de costat 50 inclinat 45º respecte a 0º.
   
 
 
Figura 5. Polígon definit mitjançant el mètode de costat, amb la segona coordenada donada mitjançant el sistema de coordenades polar
   

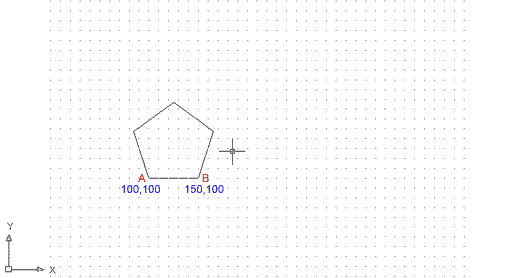
Ara feu l'experiment següent per entendre com dibuixa realment el programa un polígon a partir d'un costat.

  1. Esborreu el pentàgon anterior.
  2. Torneu a dibuixar un pentàgon pel mètode de costat, i definiu el primer punt del costat a 100,100 -l'anomenarem A- i el segon 50 unitats de dibuix a la dreta d'aquest punt, és a dir, 150,100 o bé @50,0 -l'anomenarem B.

El resultat és el següent:
   
 
 
Figura 6
   
 

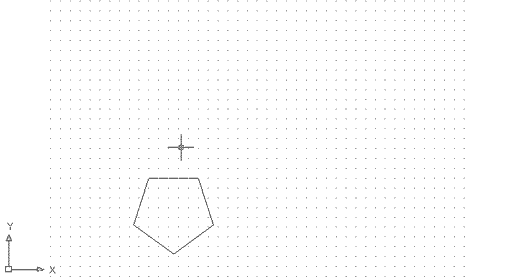
Ara feu el següent:

  1. Esborreu el pentàgon anterior.
  2. Torneu a dibuixar un pentàgon pel mètode de costat, però en aquest cas, definiu el primer punt del costat a 150,100 -la coordenada que abans anomenavem B- i el segon 50 unitats de dibuix a l'esquerra d'aquest, és a dir, 100,100 o bé @-50,0 -la coordenada que abans anomenavem A.

Ara, el resultat és aquest:
   
 
 
Figura 7
   

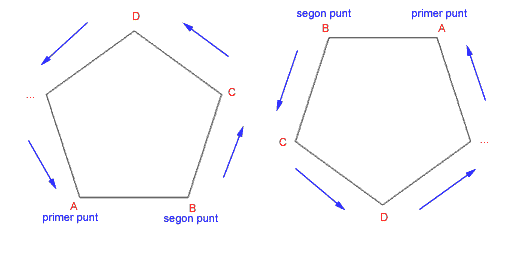
Com veieu, quan determineu un primer punt i un segon punt, el programa interpreta el tercer vèrtex, el quart, etc. del polígon en el sentit que heu fixat amb els primers dos punts. Així, tot i que les coordenades siguin les mateixes i els costats mesurin el mateix, l'ordre en què determineu els dos primers punts condiciona el resultat final.

El funcionament seria aquest:
   
 
 
Figura 8
   
  Pràcticant amb polígons
   

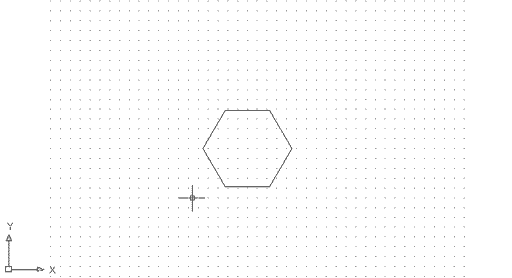
Esborreu tot el contingut de l'espai de dibuix i dibuixeu un hexàgon regular inscrit en una cicumferència amb centre a la coordenada absoluta 200,130, tal com es mostra a la figura següent:
   
 
 
Figura 9
   
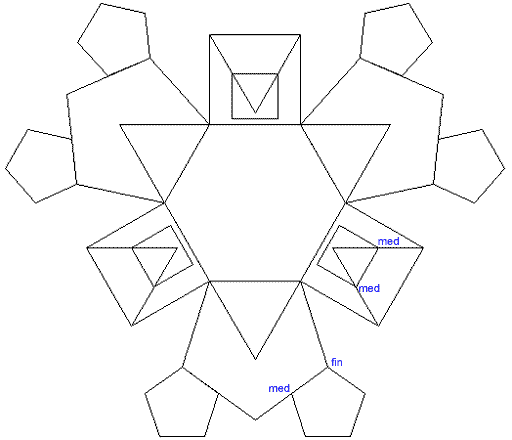
  Partint d'aquesta figura, utilitzeu l'ordre Polígono per fer el dibuix següent. Tingueu en compte que podeu determinar les coordenades mitjançant el clic directe sobre l'espai de dibuix, tot ajudant-vos de les referències a objectes que coneixeu de la pràctica anterior.
   
 
 
Figura 10
   
  Un cop fet el dibuix, deseu-lo amb el nom m1_pr9.dwg a la carpeta Practiques.
   
Referència a objectes (II): Perpendicular i Cercano
   

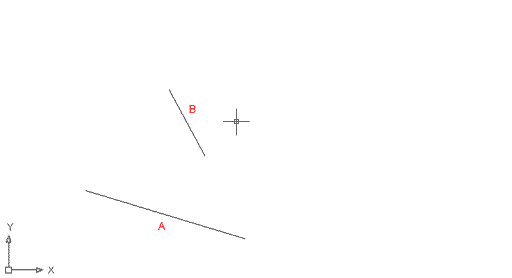
Obriu un nou document de les característiques habituals. En aquest cas, no activeu ni la Rejilla ni la Resolución; també assegureu-vos de que la funció F3 està desactivada (Comando: <RObjeto desactivado>).

Dibuixeu amb clic directe un parell de línies (A i B) com les que mostra la imatge següent:
 
 
Figura 11
   
  Referència a objectes Perpendicular
   

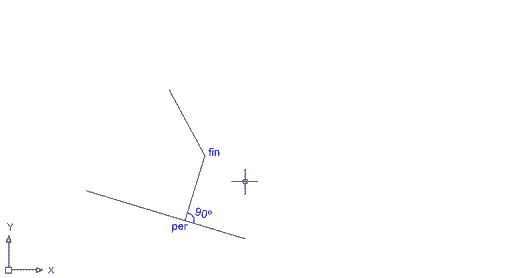
Ara dibuixareu una línia tot fent servir la referència a objectes Perpendicular, de manera que un extrem de la nova línia es trobarà, per exemple, en un punt final del segment B i l'altre sobre el segment A, essent la línia resultant perpendicular a aquest últim.

Feu el següent:

  1. Escriviu linea i premeu la tecla de Retorn.
  2. A la pregunta Precise primer punto: escriviu fin i premeu la tecla de Retorn.
  3. La barra de comandaments us respondrà de:. Apropeu el punter a l'extrem inferior del segment B i quan aparegui senyalat el punt final del segment amb el ja conegut quadrat groc, feu clic amb el botó esquerre del ratolí.
  4. Ara la barra de comandaments us demana Precise el punto siguiente o [desHacer]:. Escriviu per i premeu la tecla de Retorn o bé feu clic sobre el botó Perpendicular de la capsa d'eines Referencia a objetos. Apropeu el punter al segment A i en el moment en què aparegui un signe groc similar a aixó, , feu clic i fixeu així el segon punt de la línia.
  5. Premeu la tecla de Retorn per finalitzar l'ordre Línea.

El resultat és una línia que va des del punt final d'una altra línia fins a un segon segment, tot mantenint una relació de perpendicularitat amb aquest.
 
 

Figura 12

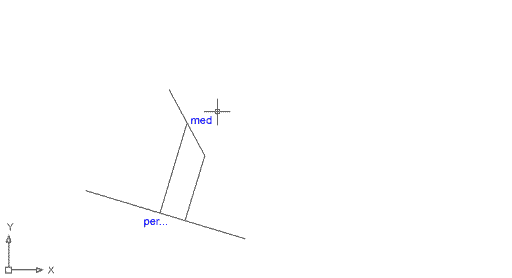
Naturalment, el procés pot ser invers. Podeu determinar primer el segment al qual ha de ser perpendicular la futura línia, i després el punt al qual ha d'arribar.

Feu una línia que vagi des de per del segment A -veureu que ara el signe groc té uns punts suspensius al darrere- fins al punt med del segment B. El resultat és una línia perpendicular al segment A que té com a extrem el punt mig del segment B.
 
 

Figura 13
   
Evidentment, si indiqueu com a primer punt un per a una línia i com a segon punt un altre per a una altra línia que no sigui paral·lela a la primera, el programa us dirà que resulta impossible fer el que li demaneu -per exemple, una línia per a A i a B.
 
Referència a objectes Cercano
   

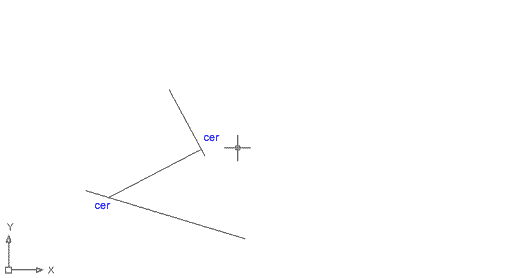
Esborreu els dos segments que van entre la línia A i la B.

Ara fareu servir la referència a objectes Cercano, que permet determinar un punt qualsevol sobre una línia recta o corba.

Feu el següent:

  1. Escriviu linea i premeu la tecla de Retorn.
  2. A la pregunta Precise primer punto: escriviu cer i premeu la tecla de Retorn o bé feu clic sobre el botó Cercano de la barra d'eines Referencia a objetos.
  3. La barra de comandaments us respondrà de:. Apropeu el punter al segment B i veureu que mentre desplaceu el punter a prop del mateix, una senyal groga com aquesta es passeja sobre la línia. En qualsevol moment podeu fer clic amb el botó esquerre del ratolí i fixar un punt d'origen sobre el segment B.
  4. Ara la barra de comandaments us demana Precise el punto siguiente o [desHacer]:. Escriviu cer i premeu la tecla de Retorn. Apropeu el punter al segment A i quan aparegui la senyal groga, feu clic.
  5. Premeu la tecla de Retorn per finalitzar l'ordre Línea.

El resultat és una línia que va des d'un punt sobre el segment B fins a un punt sobre el segment A.
 
 
Figura 14
   

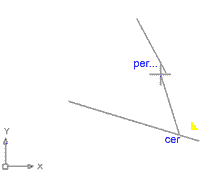
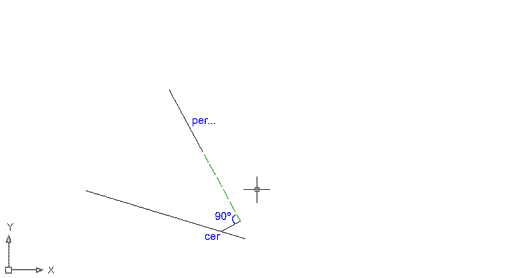
Feu la prova següent:

Dibuixeu una línia que vagi desde cer al segment A més o menys des d'on mostra la imatge, fins per al segment B -és a dir, des d'un punt sobre A des del qual seria impossible dibuixar una recta perpendicular a B. Veureu que apareix el signe groc Perpendicular flotant en l'espai de dibuix. Feu clic i veureu que, efectivament, es dibuixa una línia:

 
 
 
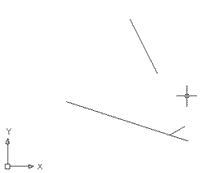
Figura 16
   
  El que ha fet el programa és una línia que va des del punt Cercano que havíeu indicat sobre la línia A fins a un punt Perpendicular no al segment de línia B, fet geomètricament impossible, sinó a la seva extensió virtual.
 
 
Figura 17
   
  Un cop feta aquesta prova, tanqueu el document sense desar els canvis i després tanqueu el programa.
   
 
Amunt