Enrera
 Mòdul 1
Dibuix tècnic amb l'AutoCAD
  Pràctica
1
2
3
4
5
6
7
8
    
Exercicis
Exercicis
 
 

Aquesta pràctica pretén introduir l'ordre de dibuix Círculo i les referències a objectes Centro, Cuadrante i Tangente.
   
L'ordre de dibuix Cercle i referències a objectes (III)
   
Dibuixar circumferències amb l'AutoCAD 2002
   

L'ordre de dibuix Círculo pot ser executada de tres maneres:

  • Fent clic al botó corresponent a l'ordre Círculo de la barra d'eines Dibujo .
  • Menú Dibujo|Círculo.
  • Mitjançant la barra de comandaments: circulo i tecla de Retorn.

Una circumferència o cercle de l'AutoCAD 2002 es pot dibuixar a partir de sis mètodes:

  • Determinant el centre i el radi del cercle.
  • Determinant el centre i el diàmetre del cercle.
  • Determinant el diàmetre a partir de dos punts.
  • Determinant tres punts.
  • Determinant dos punts de tangència i un radi.
  • Determinant tres punts de tangència.
Dibuixar un cercle a partir del seu centre
   
Pràctica

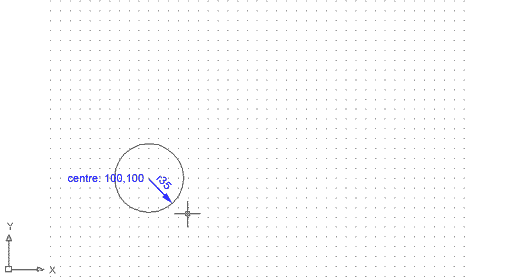
Obriu un nou document de característiques habituals. Podeu activar o no la Rejilla per visualitzar millor l'espai de dibuix i les mesures a les quals ens referirem.

Comproveu el funcionament de l'ordre Círculo en el seu primer mètode; centre/radi:

  1. Escriviu circulo a la barra de comandaments i premeu la tecla de Retorn.
  2. Un cop executada l'ordre, la barra de comandaments us demana el següent: Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)]:. ntroduïu una coordenada, per exemple 100,100, i premeu la tecla de Retorn.
  3. La barra de comandaments us demanarà Precise radio del círculo o [Diámetro]:. Introduïu un valor numèric, per exemple 35, i premeu la tecla de Retorn.

Heu fet un cercle de radi 35 unitats de dibuix amb centre a la coordenada absoluta 100,100. Evidentment, un cercle és un únic objecte, com un rectangle o un polígon.

 
 
 
Figura 1. Cercle definit mitjançant el mètode centre/radi
   
Pràctica

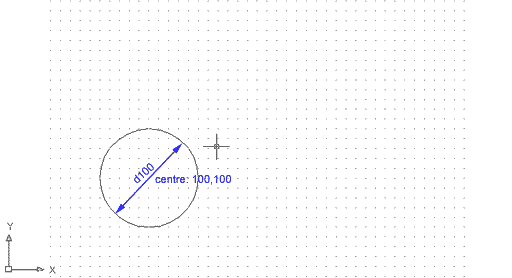
Esborreu el cercle anterior; ara fareu un cercle mitjançant el mètode centre/diàmetre:

  1. Escriviu circulo a la barra de comandaments i premeu la tecla de Retorn.
  2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <35>: responeu, com en el cas anterior, introduint una coordenada,100,100, i premeu la tecla de Retorn.
  3. La barra de comandaments us demanarà Precise radio del círculo o [Diámetro]:. Teclegeu d i premeu la tecla de Retorn.
  4. La barra de comandaments us demana ara Precise diámetro del círculo <70>: Com veieu, el diàmetre per defecte té el doble del valor del radi qua abans heu determinat. Teclegeu, per exemple, 100 i premeu la tecla de Retorn.

Heu fet un cercle de radi 50 o bé diàmetre 100, amb centre a la coordenada absoluta 100,100.

 
 
 
Figura 2. Cercle definit mitjançant el mètode centre/diàmetre
   
Dibuixar un cercle amb el mètode de dos punts
   
Pràctica

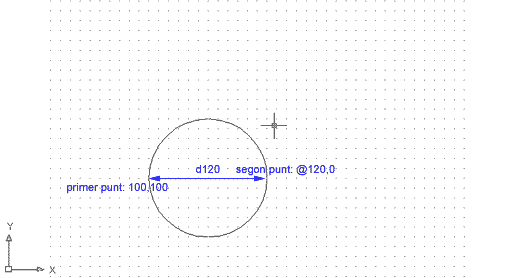
El tercer mètode, dos punts, ens permet definir un cercle a partir del seu diàmetre, sense necessitat de determinar-ne el centre. Esborreu el cercle anterior i comproveu-ho:

    1. Escriviu circulo a la barra de comandaments i premeu la tecla de Retorn.
    2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <35>: responeu 2p i premeu la tecla de Retorn.
    3. La barra de comandaments us demanarà Precise primer punto final del diámetro del círculo:. Teclegeu una coordenada, per exemple 100,100, i premeu la tecla de Retorn.
    4. La barra de comandaments us demana ara Precise segundo punto final del diámetro del círculo:. Teclegeu una segona coordenada per determinar l'altre extrem del diàmetre, per exemple @120,0, i premeu la tecla de Retorn, o bé feu clic en un segon punt de l'espai de dibuix.

Heu dibuixat un cercle de radi 60 o bé diàmetre 120, amb centre a la coordenada absoluta 160,100, a partir de l'eix que en defineix el diàmetre.

 
 
 
Figura 3. Cercle definit mitjançant el mètode de dos punts
   
Dibuixar un cercle amb el mètode de tres punts
   
Pràctica

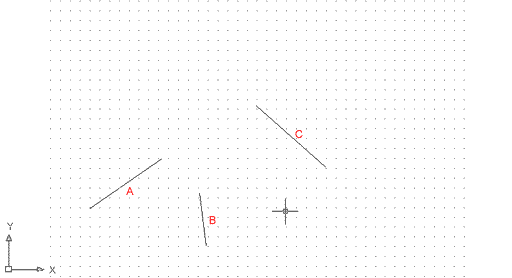
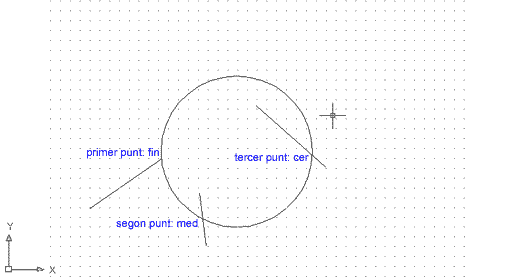
El quart mètode, tres punts, ens permet dibuixar una circumferència que passi per tres punts determinats; això no vol dir que sigui tangent a aquests tres punts. Quan en aquesta mateixa pràctica vegeu la referència a objectes Tangente, aleshores podreu especificar-ho així. Comproveu el funcionament d'aquest mètode:

    1. Esborreu el cercle anterior.
    2. Dibuixeu amb clic directe tres línies (A, B, C) semblants a les que es mostren a la imatge següent:
 
 
Figura 4
   
 
  1. Escriviu circulo a la barra de comandaments i premeu la tecla de Retorn.
  2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <35>: responeu 3p i premeu la tecla de Retorn.
  3. La barra de comandaments us demanarà Precise primer punto del círculo:. Teclegeu, per exemple, la referència a objectes fin i premeu la tecla de Retorn.
  4. La barra de comandaments us demanarà de:. Apropeu el punter a l'extrem superior del segment A i quan aparegui el quadrat groc del punt final, feu clic amb el botó esquerre del ratolí.
  5. Ara la barra de comandaments us demanarà Precise segundo punto del círculo:. Teclegeu, per exemple, la referència a objectes med i premeu la tecla de Retorn.
  6. A la pregunta de:, apropeu el punter al punt mig del segment B i quan aparegui el triangle groc del punt mig, feu clic amb el botó esquerre del ratolí.
  7. Finalment, la barra de comandaments us demanarà Precise tercer punto del círculo:. Teclegeu, per exemple, la referència a objectes cer i premeu la tecla de Retorn.
  8. A la pregunta de:, apropeu el punter a un punt qualsevol a sobre del segment C i quan aparegui el signe groc del punt proper, feu clic amb el botó esquerre del ratolí.

Heu dibuixat una circumferència que passa per tres punts determinats per vosaltres mateixos, tots desconeixent-ne el centre i el radi o diàmetre.

 
 
 
Figura 5. Cercle definit mitjançant el mètode de tres punts
   
No és necessari determinar els tres punts mitjançant referències a objectes; podeu donar tres coordenades, un clic directe i dos coordenades, una coordenada i dos punts amb referència a objectes, etc.
   
Dibuixar un cercle amb el mètode TTR (tangent, tangent, radi)
   
Pràctica

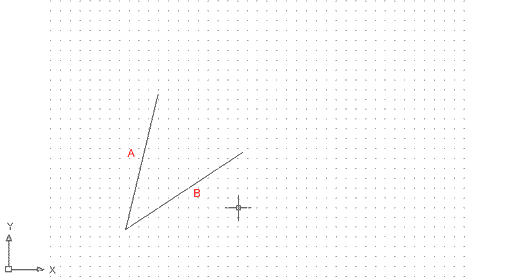
El cinquè mètode, TTR (tangent, tangent, radi), ens permet dibuixar una circumferència tangent a dos punts, amb un radi determinat. És un mètode molt còmode i que s'utilitza en nombrosos casos. Comproveu-ne el funcionament:

    1. Esborreu el dibuix anterior.
    2. Dibuixeu amb clic directe dues línies (A, B) semblants a les que es mostren a la imatge següent:
 
 
Figura 6
   
 
  1. Escriviu circulo a la barra de comandaments i premeu la tecla de Retorn.
  2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <35>: responeu ttr i premeu la tecla de Retorn.
  3. La barra de comandaments us demanarà Precise punto en objeto para la primera tangente del círculo:. Apropeu el punter al segment A i veureu que apareix un signe groc Tangente que es comporta com la referència a objectes Cercano. Feu clic sobre qualsevol punt del segment A.
  4. Ara la barra de comandaments us demanarà Precise punto en objeto para la segunda tangente del círculo:. Apropeu el punter al segment B i veureu que novament apareix el signe de tangència groc. Feu clic sobre qualsevol punt del segment B.
  5. Finalment, la barra de comandaments us demanarà Precise radio del círculo <x.xxxx>:. Introduïu un valor, per exemple 20, i premeu la tecla de Retorn.

Heu dibuixat una circumferència tangent a dues línies amb un radi de 20 unitats de dibuix.

 
 
 
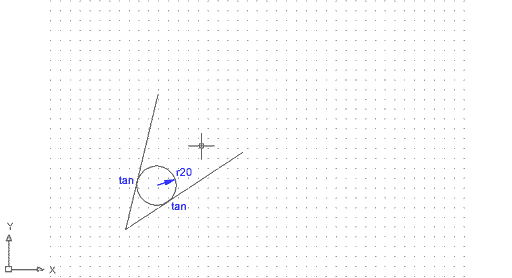Figura 7. Cercle definit mitjançant el mètode TTR (tangent, tangent, radi)
   

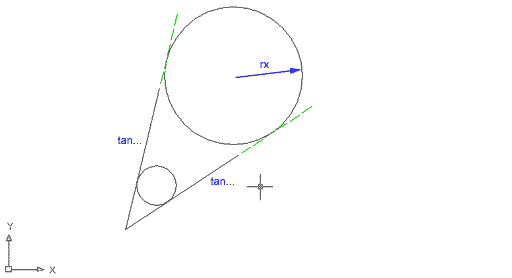
Si doneu un valor al radi massa gran perquè el cercle pugui ser efectivament tangent a les dues línies, el programa dibuixarà un cercle del radi que vosaltres indiqueu, virtualment tangent a l'extensió de les línies determinades, tal com mostra la imatge següent:
   
 
 
Figura 8
   
Dibuixar un cercle amb el mètode TTT (tangent, tangent, tangent)
   
Pràctica

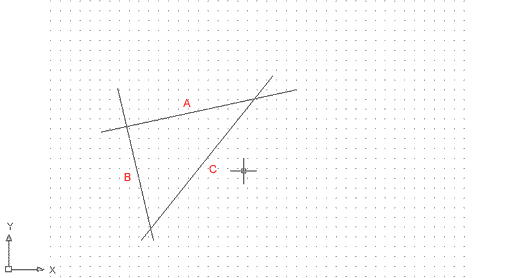
El sisè i últim mètode, TTT (tangent, tangent, tangent) ens permet dibuixar una circumferència tangent a tres punts. És en realitat una variació del mètode de tres punts, amb la particularitat que els tres punts ens qüestió són punts de tangència; per tant, si utilitzeu el mètode de tres punts i feu servir tres vegades la referència a objectes Tangente -que immediatament veureu-, en realitat esteu fent servir el mètode TTT. Comproveu-ne el funcionament:

    1. Esborreu el dibuix anterior.
    2. Dibuixeu amb clic directe tres línies (A, B, C) semblants a les que es mostren a la imatge següent:
 
 
Figura 9
   
 
  1. Activeu el menú Dibujo|círculo|Tan, tan, tan (TTT).
  2. La barra de comandaments us demanarà directament Precise primer punto del círculo: tan a. Apropeu el punter al segment A i quan aparegui el signe de tangència groc, feu clic amb el botó esquerre del ratolí.
  3. Ara la barra de comandaments us demanarà Precise segundo punto del círculo: tan a . Apropeu el punter al segment B i quan aparegui el signe de tangència groc, feu clic amb el botó esquerre del ratolí.
  4. Per últim, la barra de comandaments us demanarà Precise tercer punto del círculo: tan a . Apropeu el punter al segment C i quan aparegui el signe de tangència groc, feu clic amb el botó esquerre del ratolí.

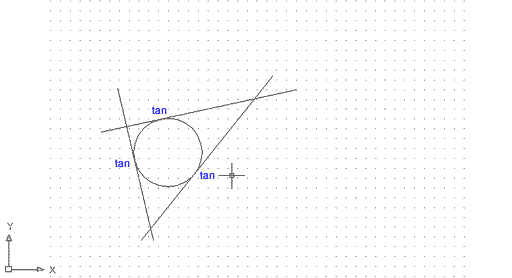
Heu dibuixat una circumferència tangent a tres segments, tot desconeixent-ne el centre i el radi o diàmetre.

 
 
Figura 10. Cercle definit mitjançant el mètode TTT (tangent, tangent, tangent)
   
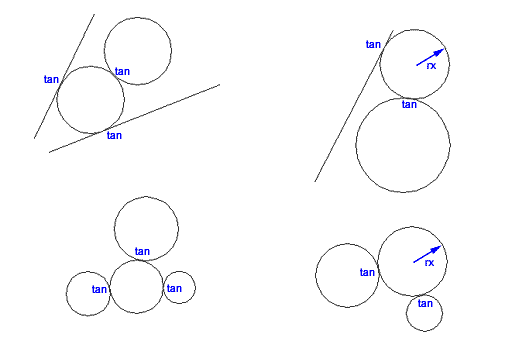
Naturalment, no és necessari que el cercle sigui tangent a tres línies rectes; pot ser tangent a dues rectes i un cercle, tres cercles, una recta i dos cercles, etc. Això també és vàlid per al mètode TTR.
   
 
 
Figura 11
   
  Referències a objectes Centro, Cuadrante i Tangente
   
Referència a objectes Centro
   
Pràctica

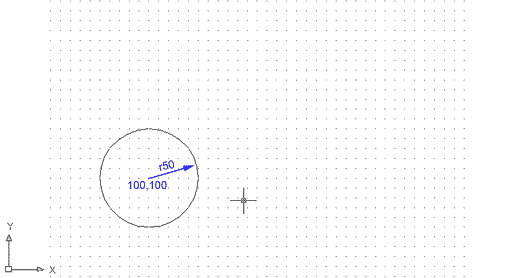
Esborreu tot el dibuix anterior i feu un cercle de radi 50 amb centre a la coordenada absoluta 100,100.
 
 
 
Figura 12
   
 

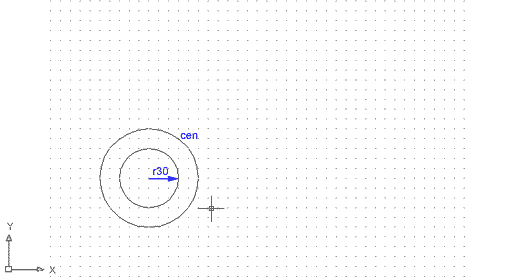
Ara dibuixareu un cercle concèntric de radi 30, tot fent servir la referència a objectes Centre.

Feu el següent:

  1. Escriviu circulo i premeu la tecla de Retorn.
  2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <x.xxx>: escriviu cen i premeu la tecla de Retorn o bé feu clic al botó Centro de la capsa d'eines Referencias a objetos.
  3. La barra de comandaments us respondrà de:. Apropeu el punter a la circumferència i quan n'aparegui senyalat el centre amb un cercle groc , feu clic amb el botó esquerre del ratolí.
  4. Ara la barra de comandaments us demana Precise radio del círculo o [Diámetro]:. Escriviu 30 i premeu la tecla de Retorn.
Heu fet una circumferència concèntrica a una primera, prenent com a referència el seu propi centre.
 
 

Figura 14

Òbviament, el centre és una referència a objectes com qualsevol altra, i des d'ella es pot dibuixar un objecte, com per exemple una línia o un polígon (línia des de centre d'una circumferència a coordenada, o de coordenada a centre; polígon inscrit en una circumferencia amb centre al centre d'una circumferència ja existent, etc.).
 

 
Pràctica
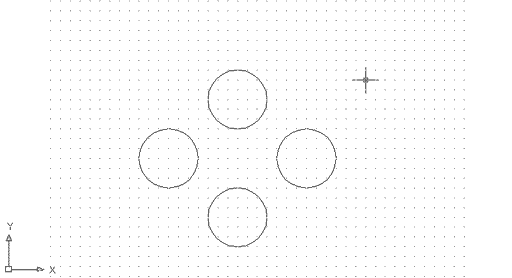
 Esborreu els dos cercles anteriors i dibuixeu quatre cercles de 30 unitats de dibuix de radi, amb centre a les coordenades: 120,120, 190,180, 260,120, 190,60 tal com mostra la imatge:
   
 
 
Figura 15
   
Pràctica
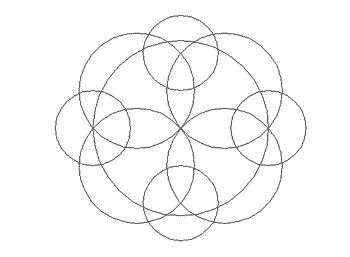
 Ara, tot fent servir l'eina de dibuix Círculo i la referència a objectes Centro, dibuixeu la figura següent:
   
 
 
Figura 16
   
  Deseu el resultat amb el nom m1_pr7a.dwg a la carpeta Practiques.
   
Referència a objectes Cuadrante
   
Pràctica

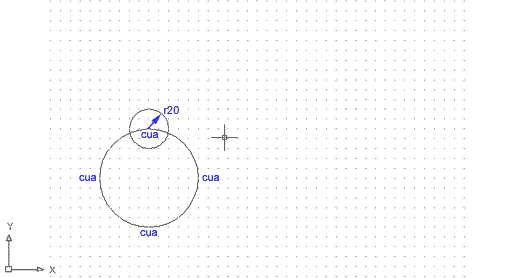
Obriu un nou document de les característiques habituals i dibuixeu un cercle de radi 50 amb centre a la coordenada absoluta 100,100.

Ara fareu servir la referència a objectes Cuadrante:

  1. Escriviu circulo i premeu la tecla de Retorn.
  2. A la pregunta Precise punto central para círculo o [3P/2P/Ttr (tangente tangente radio)] <x.xxx>: escriviu cua i premeu la tecla de Retorn o bé feu clic al botó Cuadrante de la capsa d'eines Referencias a objetos.
  3. La barra de comandaments us respondrà de:. Apropeu el punter a la circumferència i veureu que apareix un rombe groc quan us trobeu a prop de l'angle 0º, 90º, 180º o 270º de la circumferència. Aquestes quatre posicions són els quatre quadrants dels cercles. Feu clic amb el botó esquerre del ratolí quan us trobeu al quadrant 90º.
  4. Ara la barra de comandaments us demana Precise radio del círculo o [Diámetro]:. Escriviu 20 i premeu la tecla de Retorn.

Heu fet una circumferència de 20 unitats de dibuix, amb centre al quadrant 90º d'una circumferència preexistent.
 
 
Figura 17
   
Pràctica
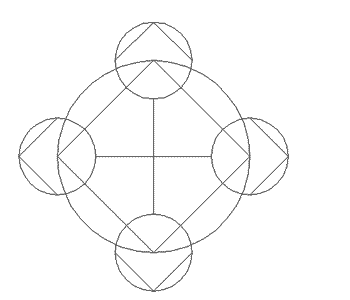
 Ara, tot fent servir l'eina de dibuix Círculo i Línea i la referència a objectes Cuadrante, dibuixeu la figura següent:
   
 
 
Figura 18
   
  Guardeu el resultat amb el nom m1_pr7b.dwg a la carpeta Practiques.
   
Referència a objectes Tangente
   
Pràctica

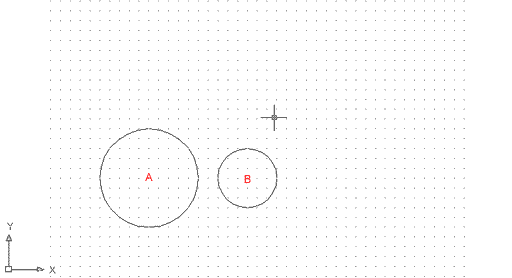
Obriu un nou document de les característiques habituals, dibuixeu una circumferència de radi 50 amb centre a la coordenada absoluta 100,100 (A), i una altra circumferència de radi 30 a la coordenada absoluta 200,100 (B).
   
 
 
Figura 19
   
 

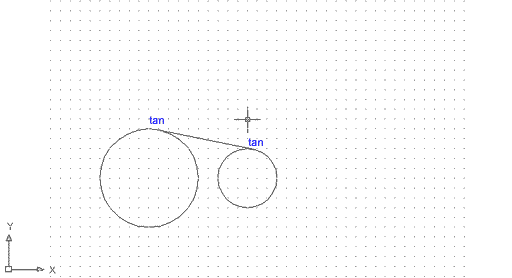
Ara fareu servir la referència a objectes Tangente:

  1. Escriviu linea i premeu la tecla de Retorn.
  2. A la pregunta Precise primer punto: escriviu tan i premeu la tecla de Retorn o bé feu clic al botó Tangente de la capsa d'eines Referencias a objetos.
  3. La barra de comandaments us respondrà de:. Apropeu el punter a la part superior -entre el grau 0º i el 180º- de circumferència A i veureu que apareix el senyal groc de tangència que ja coneixeu. Feu clic amb el botó esquerre del ratolí.
  4. Ara la barra de comandaments us demana Precise el punto siguiente o [desHacer]:. Escriviu tan i premeu la tecla de Retorn.
  5. La barra de comandaments us respondrà de: Apropeu el punter a la part superior -entre el grau 0º i el 180º- de circumferència B, i quan vegeu el senyal groc de tangència, feu clic amb el botó esquerre del ratolí.
 
 
Figura 20
   
 

Ara repetiu l'operació, seguint les indicacions següents:

  1. Escriviu linea i premeu la tecla de Retorn.
  2. A la pregunta Precise primer punto: escriviu tan i premeu la tecla de Retorn.
  3. La barra de comandaments us respondrà de: Apropeu el punter a la part superior de la circumferència A i feu clic amb el botó esquerre del ratolí quan aparegui el senyal de tangència.
  4. Novament, la barra de comandaments us demana Precise el punto siguiente o [desHacer]:. Escriviu tan i premeu la tecla de Retorn.
  5. La barra de comandaments us respondrà de:. Apropeu el punter a la part INFERIOR, entre el grau 180º i el 360º de la circumferència B, i quan vegeu el senyal groc de tangència, feu clic amb el botó esquerre del ratolí.

El resultat és el següent:
 
 
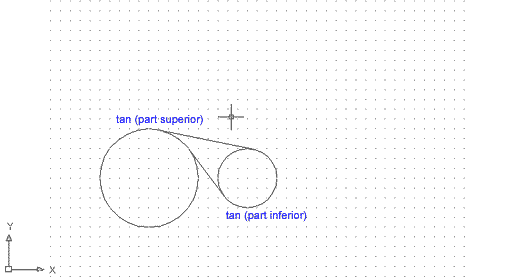Figura 21
   
És important on es marca el punt de tangència d'una línia respecte a una circumferència, si s'indica per sobre de la meitat o per sota, tant el punt primer com el punt segon. Seria exactament vàlid per dues circumferències una a sobre de l'altra, tot indicant els punts de tangència a la dreta o a l'esquerra.
   
  Tanqueu el document sense desar els canvis i sortiu del programa.
   
 
Amunt