Fractals geomètrics simples
Les característiques dels fractals
Quan Mandelbrot va "inventar" el mot fractal, el va utilitzar per designar aquesta serie d'objectes geomètrics d'estructura irregular. Mandelbrot no va donar una definició precisa de fractal però va caracteritzar les noves figures amb les tres propietats següents:
- Figures auto similars. És a dir figures que tenen una estructura tal que dins ella mateixa, l'estructura, es repeteix infinites vegades a escales més petites.
- Figures amb dimensió fraccionària (no entera). Figures massa complexes per tractar-se només d'un punt, una línia, un pla o un volum, figures que sobrepassen els nivells de la seva dimensió física i per tant tenen una dimensió superior a ella.
- Conjunts que apareixen després de processos iteratius infinits. (Figures que apareixen al repetir en elles mateixes un mateix procés per tal d'aconseguir l'auto similitud.)
El conjunt de Cantor
El conjunt de Cantor, introduït pel matemàtic alemany Georg Cantor 
, és un conjunt fractal que es construeix dividint un segment en tres parts i suprimint el segment central. Tot seguit es procedeix a fer el mateix als segments laterals restants i així indefinidament. De manera que queda un seguit de punts tots situats sobre l'antic segment.
Els punts són abstractes i per tant irrepresentables però podem realitzer un gràfic del procés iteratiu que conforma el conjunt de Cantor fins a la sisena repetició (iteració):
La corba i el floc de neu de Koch
Una corba de Koch és un objecte fractal que té la propietat de tenir longitud infinita, ser alhora contínua i de no ser derivable en cap dels seus punts. Va ser construïda per Helge von Koch el 1904 i va ser una de les primeres corbes fractals que es van divulgar.
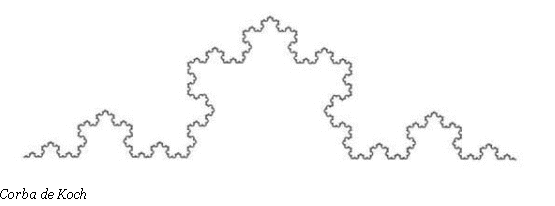
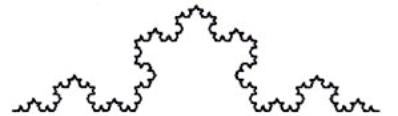
Per construir la corba de Koch s'ha de seguir un algoritme simple partint d'un segment al que s'ha de substituir per quatre segments de mida 1/3 de la mida del segment inicial. Aquests segments es col·loquen de manera que el terç central del segment mare sigui ocupat per dos dels segments petits formant un triangle equilàter sense la base inferior. Seguidament es repeteix el mateix procés en cada un dels segments restants. La corba de Koch és el resultat de seguir el procediment anterior infinitament.
La corba de Koch també pot ser representada pel sistema L-system com comprovarem.
El segment inicial:
La primera iteració:
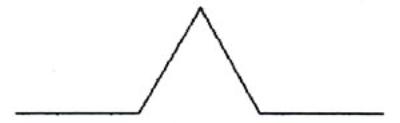
La segona iteració:
La tercera iteració:
La quarta iteració:
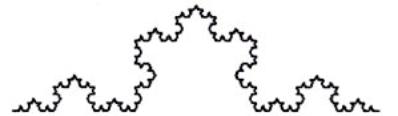
La cinquena iteració:
El floc de neu de Koch o estrella de Koch és un conjunt geomètric fractal publicat al mateix any i pel mateix autor que la corba de Koch. Aquesta figura està formada per un triangle equilàter cada un dels costats del qual està format per una corba de Koch. L'àrea del floc de neu de Koch és 8/5 de l'àrea del triangle inicial, per tant, un perímetre infinit format per les tres corbes de Koch, obtingudes iterant la funció als tres costats del triangle equilàter, engloba una àrea finita.
Triangle, tetraedre i quadrat de Sierpinski
El triangle de Sierpinski és un objecte fractal, que va ser introduït el 1915 pel matemàtic polonès Waclaw Sierpinski . Es pot construir a partir de qualsevol triangle encara que inicialment es va construir a partir d'un triangle equilàter.
Per a la seva construcció es segueix el següent algorisme:
- Un triangle inicial, es divideix en quatre triangles unint els punts mitjans dels seus costats
- S'elimina el triangle interior
- En cada un dels tres triangles restants es procedeix a fer el pas 1
Una altra manera d'originar el triangle de Sierpinski és a través d'un sistema d'iteració de funcions basat en la substitució, anomenat L-system, que explicarem més endavant.
La àrea d'aquest triangle iterat infinites vegades és zero, ja que cada cop que iterem l'àrea es redueix a 3/4 de l'anterior i per tant iterat moltes vegades, l'àrea tendeix a zero.
El Tetraedre de Sierpinski és la versió tridimensional del triangle de Sierpinski. Ja que es parteix d'un tetraedre regular i es divideix en tetraedres de costat meitat i s'eliminen els que no són a les puntes. Seguidament s'itera el procediment en els tetraedres restants.
El quadrat de Sierpinski és un objecte pla fractal descrit per Waclaw Sierpinski el 1916. El quadrat és una generalització del Conjunt de Cantor en dos dimensions.
Per construir-lo, s'ha de començar amb un quadrat que és dividit en nou quadrats iguals, tres per banda i un al centre el qual és eliminat. Seguidament s'itera l'operació en els vuit quadrats restants.
Quadrat de Sierpinski
L'esponja de Menger
L'esponja de Menger és una versió tridimensional del Conjunt de Cantor o del Quadrat de Sierpinski. Va ser descrit per un matemàtic austríac anomenat Parl Menger el 1926.
Per construir-lo s'ha de començar des d'un cub, i dividir-lo en 27 petits cubs (9 per costat i un al centre). Com es feia al construir el quadrat de Sierpinski, s'elimina el cub central de cada cara i el del centre, així, queden 20 cubs iguals en els quals es repeteix l'operació anterior infinitament.
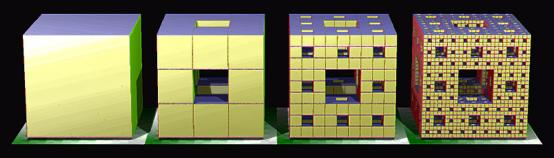
Primeres iteracions de l'Esponja de Menger
El nombre de cubs de la formació en cada noment es pot trobar amb: 20 n . On n és el nombre d'iteracions (vegades que s'ha repetit el procés explicat):
0 i teracions --> 1 cub
1 iteracions --> 20 cubs
2 iteracions --> 400 cubs
3 iteracions --> 8.000 cubs
4 iteracions --> 160.000 cubs
5 iteracions --> 3.200.000 cubs
6 iteracions --> 64.000.000 cubs
Les corbes de Peano i Hilbert
El 1890, Giuseppe Peano va construir un corba contínua que passa per tots els punts del quadrat unitat. Era el primer exemple d'una corba que omple un espai. Anys més tard David Hilbert va construir-ne una de la mateixa naturalesa més simple de descriure.
La corba de Hilbert es construeix dividint el un quadrat del que es parteix en quatre quadrats més petits i unint els centres de cada quadrat amb una línia contínua que comença al centre del quadrat inferior esquerre i acaba al quadrat inferior dret. Tot seguit es repeteix l'operació a cada quadrat de mida 1/2 de l'inicial substituint el tros de corba ja existent per la corresponent a l'operació.
Es continua indefinidament amb aquest procés unint els centres dels quadrats que apareixen a cada etapa.
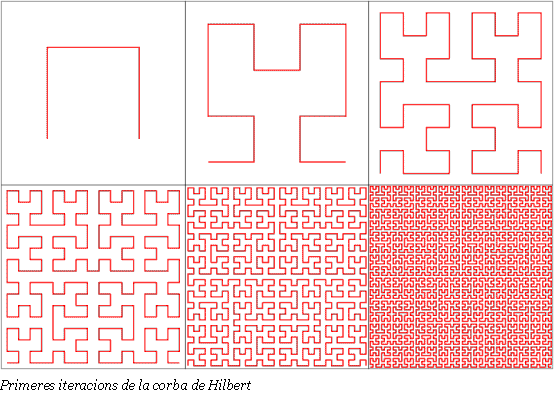
La corba resultat d'iterar infinitament aquesta formula omple el quadrat unitat i rep el nom de corba de Hilbert.
La corba de Peano , es construeix de manera molt similar a la corba de Hilbert.
Un quadrat es divideix en 9 quadrats més petits i iguals i en cada un d'ells es dibuixa una corba com la representada en la primera casella. Al iterar dos vegades aquesta funció s'obté una corba com la de la tercera casella.
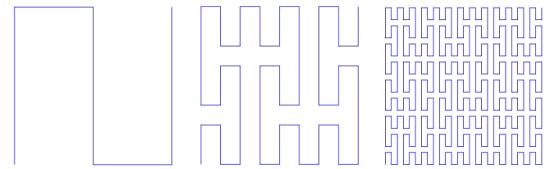
Primeres iteracions de la corba de Peano
Com hem dit abans, si iterem indefinidament aquests dos processos, obtindrem simplement un pla, una figura de dimensió 2.