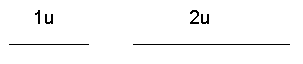31.01.2002
|
Què
entenem per dimensió generalment?
|


|
El punt no el podem representar perquè és abstracte Però això no és pas una definició matemàtica. Matemàticament veiem que:
Per tant podríem dir que la dimensió és la quantitat de números reals que es necessiten per definir un punt dintre de cada objecte. Ara ens mirem el concepte de dimensió des d'un altre punt de vista. Cal mirar la dimensió d'una altre manera per poder generalitzar i arribar a un definició que pugui donar un resultat no enter, com sabem que passa amb les dimensions de les fractals. Perquè la definició anterior no ens serveix per generalitzar-la. Tenim un segment,
que mesura una unitat. Quan multipliquem la unitat per 2, aquest
objecte geomètric (segment) queda multiplicat per 2, 2 =
2^1
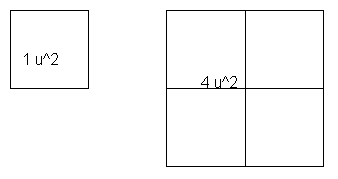
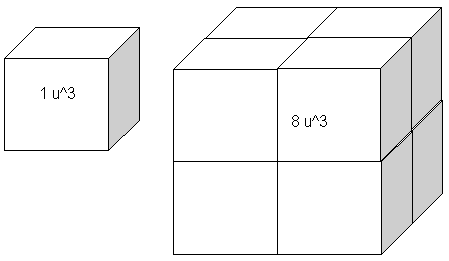
Fem el mateix
amb el cub, si primer construïm un cub de costat unitat i llavors
l'ampliem a un cub amb la unitat el doble de gran que la primera,
el segon cub quedarà multiplicat per 8, 8=2^3
Observem doncs, que la dimensió es pot definir com un exponent, i un exponent és un logaritme, concretament aquest és un logaritme de base 2. Ens adonem que aquest factor 2 pel qual multipliquem la unitat, el podem escriure com P/p, on P és la mesura de la unitat gran i p la mesura de la unitat petita, agafant una unitat de mesura comuna qualsevol per comparar-les. Podríem anomenar N al número de vegades que la figura ampliada conté a la figura inicial. I per tant podem dir que N és el quocient entre el número d'unitats que mesura la figura "ampliada" i el número d'unitats que mesura la figura "inicial", utilitzant una unitat de mesura comuna. Si ens ho mirem
en el cub, veiem que:
La dimensió
del cub hem vist que és 3, i hem vist també que 2^3
= 8, per tant Apliquem les propietats dels logaritmes i ens adonem que:
Ara
ja tenim una fórmula general que ens permet calcular dimensions,
tan si són fraccionàries com si són enteres Dim
= log (N)/Log (P/p) |
![]()