|
-
Les
del primer tipus s'anomenen Algorismes d'Escapament.
Per a cada punt es calculen una sèrie de valors mitjançant
la repetició d'una fórmula fins que es compleix
una condició, moment en el qual se li assigna al punt
un color relacionat amb el nombre de repeticions. La fractal
de Mandelbrot és generada per aquest tipus d'algoritmes.
La fractal de Mandelbrot, els ordinadors la generen fent servir
els següents tipus de càlculs:

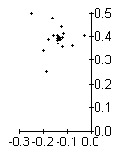

Si
representem gràficament la seqüència de z's
que hem aconseguit amb c = -0.2 + 0.8i, tenim el següent
gràfic:
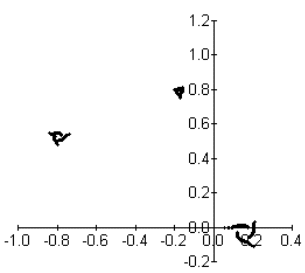
Ens
adonem que aquesta seqüència de z's no fa un espiral
a un punt. Enlloc d'això, crea un conjunt d'espirals
que fan espiral en 3 punts diferents.
Resum del comportament:
Amb c = 0.5i, l'espiral de z's cau en un sol punt. Amb c = -0.2
+ 0.8i, l'espiral de z's cau en 3 punts diferents. Amb c = -3
o c=1, el conjunt de z's creix molt ràpid.
El més interessant de les c's es que no provoquen que
les z's creixin molt ràpid (exemple, c = 0.5i i c = -0.2
+ 0.8i no provoca un ràpid creixement de z's, però
c = -3 i c = 1 sí que ho provoca.). Ara fem la gràfica
de tots els valors de c en un pla complex en el que puguem veure
el conjunt de z's sense que creixi massa ràpidament:

Aquest conjunt de nombres complexes és l'anomenat conjunt
de Mandelbrot.
A l'hora de pintar les diferents zones, es pinta amb diferents
colors els punts depenent del nombre de vegades que s'hagi de
repetir la fórmula per aconseguir que el valor del mòdul
del nombre complex resultant sigui més gran que el del
nombre complex inicial
La fractal de Mandelbrot és una de les més conegudes
i més boniques. Per tal de demostrar la propietat d'autosemblança
de les fractals, he agafat un programa d'ordinador en el qual
hi ha la fractal de Mandelbrot inicialment, i es pot agafar-ne
un tros i ampliar-la. Fent això he obtingut els següents
dibuixos:
Autosemblaça en el conjunt
de Mandelbrot:
En aquesta
successió d'imatges es pot apreciar com
agafant una petita part de fractal original, i ampliant-la,
ens tornem a trobar amb el dibuix original:
Clica la imatge per veure les succesives ampliacions: 
Agafant un altre tros de la figura original passa el mateix
com podeu veure en aquestes altres successions d'imatges:

Si poguéssim anar ampliant petits detalls de cada imatge,
segur que trobaríem l'imatge original molts cops, i segur
també que altres vegades cauríem en taques negres
on no es troba res. De totes maneres ho hauríem de fer
amb un altre programa perquè aquest només permet
5 ampliacions.
Aquest
Gif animat il·lustra la idea anterior molt millor que qualsevol
imatge fixa:

El que us
mostro a continuació és un seguit d'imatges molt
boniques que trobem fent ampliacions al conjunt de Mandelbrot.
Aquestes imatges han estat trobades amb el programa fractint.
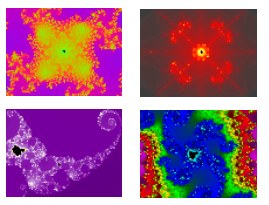
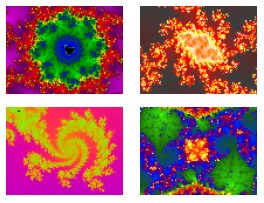

Aquí
hi ha una col·lecció
d'imatges de la fractal de Mandelbrot, obtingudes per ampliacions
successives, mitjançant un programa en Visual Basic creat
per el meu tutor del treball de recerca, Xavier Codolà.

- El
segon tipus és el de les funcions Iterades(IFS).
Va ser creat per M. Barsnsley. El sistema de funcions iterades
(IFS) es basa en el principi d'autosemblança. En una fractal
IFS sempre es pot trobar una part de la figura que guarda una
relació de semblança amb la figura completa. Si
amb una lupa veiéssim qualsevol fulla petita ens adonaríem
que és gairabé igual a la branca completa. Aquest
tipus de fractals comparteixen moltes semblances amb molts objectes
reals de la natura, per això podem dir que la fulla és
una funció iterada, perquè la podem trobar a la
natura o la podem crear iterant una funció.
La complexitat d'aquestes imatges existeix, perquè és
bàsicament un gran nombre de repeticions de la mateixa
imatge. Això treu partit d'un dels teoremes, que encara
que no estigui matemàticament demostrat, diu que si vas
fent zoom contínuament a una imatge fractal, es repeteix
ella mateixa amb imatges semblants.

Aquesta imatge ha estat treta de
www.calweb.com/~bjohnson/
Brad Johnson.

- Un
altre tipus és l'anomenat de Lindenmayer y Sierpinski,
anomenat així perquè són els noms de les
fractals més conegudes d'aquest tipus. Es tracta d'un triangle
en el qual se'n hi allotja un altre, format per la unió
de tots els punts mitjos dels seus costats. Això es repeteix
amb tots i cada un dels triangles formats que tinguin la mateixa
orientació que l'original, i així successivament.
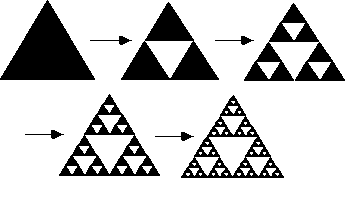
El triangle de Sierpinski és una de les poques fractals
que es pot dibuixar amb exactitud i sense ajuda d'un ordinador,
seguint les instruccions anteriors. El triangle de Sierpinski
és un exemple de fractal molt fàcil de crear i d'entendre.
En la figura 6 es veu molt clarament el procés de construcció
d'aquest triangle. Aquest procés es va repetint un nombre
infinit de vegades.
Un
altre exemple de fractals d'aquest tipus és la corba
de koch i el triangle de koch. La corba es forma partint d'un
segment que dividim en tres parts iguals. La part central es substitueix
per dos sements del mateix tamany que l'eliminat. Es va repetint
el mateix successivament per cada segment format. La longitud
d'aquesta corba evoluciona d'acord amb la següent successió:
1, 4/3, 16/9, 64/27, 256/81... , L=(4/3)^k. Aquesta corba té
una longitud infinita perquè la successió anterior
tendeix a infinit. El triangle de Koch es forma quan tenim un
triangle equilàter i a cada costat fem el que hem explicat
sobre la corba. El triangle de Koch s'anomena també
floquet de neu, perquè té una forma que ens
recorda aquestes figures de la naturalesa.


- El
següent tipus, és l'anomenat Òrbites Caòtiques.
Aquest tipus de model va néixer amb l'estudi d'òrbites
caòtiques desenvolupat per E. Lorenz. Sabem des dels primers
anys d'estudi que els planetes descriuen òrbites el·líptiques.
Com en tot, això és cert només fins a cert
punt. L'atractor de Lorenz s'aconsegueix portant aquesta incertitud
fins a l'extrem. Considero que explicar els atractors de Lorenz
seria massa complicat, i difícil d'entendre, per això
el que he fet és descriure un programa que he trobat sobre
els atractors, que és senzill d'utilitzar
i no tant difícil d'entendre com els atractors de Lorenz.

- L'últim
tipus és l'anomenat Aleatoris i Cel·lulars.
Estructures com el plasma o les imatges de difusió depenen
en cert grau de l'atzar, per tant són úniques i
irrepetibles. Els autòmats cel·lulars estan a l'altre
extrem. Funcionen amb senzilles regles que pinten zones a partir
del color de les adjacents. Encara que en principi pugui semblar
que les imatges aconseguides amb aquest mètode seran senzilles
i simètriques, no té perquè ser així.
D'aquest tipus no n'explicaré cap exemple perquè
són massa complicats, i no són massa importants
per entendre què són les fractals.

Tots els tipus
de fractals segons la manera de generar-se, tenen coses en comú,
però les agrupem segons si la característica més
important que tenen és d'un grup o d'un altre.
|



![]()